Навигация
Метод геометрических преобразований
4.2 Метод геометрических преобразований
4.2.5 Метод подобия
Задача. Построить трапецию ABCD по углу А и основанию ВС, если известно, что AB:CD:AD = 1:2:3.
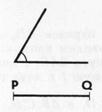
Рис. 4
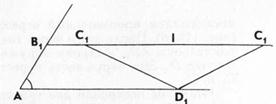
Рис. 5
Решение. Задачу надо понимать так: даны угол hk и отрезок PQ (рис. 4). Требуется построить с помощью циркуля и линейки трапецию ABCD, у которой ![]() A =
A = ![]() hk, BC = PQ, а остальные три стороны АВ, CD и AD относятся как 1:2:3. Построим сначала какую-нибудь трапецию AB1C1D1, у которой
hk, BC = PQ, а остальные три стороны АВ, CD и AD относятся как 1:2:3. Построим сначала какую-нибудь трапецию AB1C1D1, у которой ![]() А =
А = ![]() hk и AB1:C1D1:AD1 = 1:2:3. Это сделать совсем не трудно. Строим угол А, равный данному углу, и на его сторонах откладываем произвольный отрезок АВ1 и отрезок AD1 = 3AB1(рис. 5). После этого через точку В1, проводим прямую l, параллельную AD1 и строим окружность радиуса 2АВ1, с центром в точке D1,. Эта окружность пересекает прямую l в двух точках С1 и C1'.
hk и AB1:C1D1:AD1 = 1:2:3. Это сделать совсем не трудно. Строим угол А, равный данному углу, и на его сторонах откладываем произвольный отрезок АВ1 и отрезок AD1 = 3AB1(рис. 5). После этого через точку В1, проводим прямую l, параллельную AD1 и строим окружность радиуса 2АВ1, с центром в точке D1,. Эта окружность пересекает прямую l в двух точках С1 и C1'.
Итак, мы построили две трапеции AB1C1Dl и АВ1С1'D1, у которых ![]() A =
A = ![]() hk и стороны АВ1, ВС1 (В1С1') и C1Dl (С1'D1) относятся как 1:2:3.
hk и стороны АВ1, ВС1 (В1С1') и C1Dl (С1'D1) относятся как 1:2:3.
Возьмем одну из этих трапеций, например, AB1C1Dl, проведем прямую АС1, и построим отрезок ВС с концами на сторонах угла В1АС1, который параллелен B1C1 и равен PQ. Это можно сделать так: на луче AD1 откладываем отрезок AE = PQ и через точку Е проводим прямую, параллельную AB1. Она пересекается с прямой АС1 в точке С (рис. 6). Через точку С проводим прямую, параллельную B1C1, и получаем точку В. Очевидно, отрезок ВС равен PQ. Остается провести через точку С прямую, параллельную C1Dl. Она пересекает луч AD1, в точке D. Трапеция ABCD искомая. В самом деле, ![]() А =
А = ![]() hk, BC = PQ и
hk, BC = PQ и ![]() (это следует из подобия треугольников ABC и AB1C1, ACD и AС1D1). Отсюда получаем, что AB:СD:AD = AB1:C1D1:AD1 = 1:2:3.
(это следует из подобия треугольников ABC и AB1C1, ACD и AС1D1). Отсюда получаем, что AB:СD:AD = AB1:C1D1:AD1 = 1:2:3.
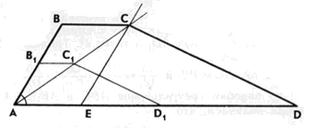
Рис. 6
Построенная трапеция ABCD удовлетворяет всем условиям задачи. Если вместо трапеции AB1C1Dl взять трапецию АВ1С1'D1 и проделать такие же построения, то получим второе решение задачи (рис. 7). Итак, данная задача имеет два решения [4].
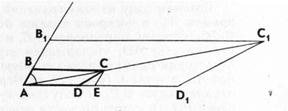
Рис. 7
4.3. Алгебраический метод
Пример. Из вершин данного треугольника как из центров описать три окружности, касающиеся попарно внешним образом.
Пусть ABC (рис. 8) — данный треугольник, а, b, с — его стороны, х, у и z — радиусы искомых окружностей.
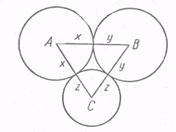
Рис. 8
Выразим длины отрезков х, у, z через длины известных отрезков а, b, с. Тогда х+у=с, y+z=a, z+x=b. Поэтому 2х+2у+2z = a+b+c, x+y+z=![]() (a+b+c), откуда
(a+b+c), откуда ![]() .
.
Строим теперь один из найденных отрезков, например х, по формуле ![]() и проводим окружность (A, х). Две другие окружности проводим из центров В и С радиусами соответственно с — х и b — х.
и проводим окружность (A, х). Две другие окружности проводим из центров В и С радиусами соответственно с — х и b — х.
Для доказательства достаточно заметить теперь, что две последние окружности касаются между собой, так как сумма их радиусов (с — х) + (b — х) = с + b — 2х = (с + b) — (с + b — а) = а = ВС, то есть равна расстоянию между их центрами.
Задача всегда однозначно разрешима, так как:
1) в треугольнике ABC b+c>a, и поэтому отрезок x может быть построен;
2) с>х, потому что с — х = ![]() (так как а+с>b);
(так как а+с>b);
3) b>х, потому что b – х = ![]() >0 [2].
>0 [2].
Приложение 5
Психологические методики
МЕТОДИКА “ОБРАЗОВАНИЕ ПРОСТЫХ АНАЛОГИЙ” [9]
Под №1 слева написано два слова: сверху лошадь, внизу жеребенок. Какая между ними связь? Жеребенок – детеныш лошади. А справа под №1 тоже одно слово корова, а снизу 5 слов на выбор. Из них нужно выбрать только одно, которое будет так же относиться к слову корова, как жеребенок к лошади, т.е. чтобы оно обозначало детеныша коровы. Это будет теленок. Подчеркиваем слово теленок. Итак, нужно сначала установить, как связаны между собой слова, написанные слева, и затем установить такую же связь справа. Так же решаются все задачи.
| 1. Лошадь | Корова |
|
| Жеребенок 2. Школа | Пастбище, рога, молоко, теленок, бык Больница | |
| Обучение 3. Яйцо | Доктор, ученик, учреждение, лечение, больной Картофель | |
| Скорлупа 4. Ложка | Курица, огород, капуста, суп, шелуха Вилка | |
| Каша 5. Коньки | Масло, нож, тарелка, мясо, посуда Лодка | |
| Зима 6. Ухо | Лед, каток, весна, лето, река Зубы | |
| Слышать 7. Собака | Видеть, лечить, рот, щетка, жевать Щука | |
| Шерсть 8. Пробка | Овца, ловкость, рыба, удочки, чешуя Камень | |
| Плавать 9. Чай | Пловец, тонуть, гранит, возить, каменщик Суп | |
| Сахар 10. Дерево | Вода, тарелка, крупа, соль, ложка Рука | |
| Сук 11 Дождь | Топор, перчатка, нога, палец, работа Мороз | |
| Зонтик 12. Песня | Палка, холод, сани, зима, шуба Картина | |
| Глухой 13. Нож | Хромой, слепой, художник, рисунок, больной Стол | |
| Сталь 14. Рыба | Вилка, дерево, стул, пища, скатерть Муха | |
| Сеть 15. Утро | Решето, комар комната, жужжать, паутина Зима | |
| Ночь 16. Птица | Мороз, день, январь, осень, сани Человек | |
| Гнездо | Люди, птенец, рабочий, зверь, дом | |
КЛЮЧ К МЕТОДИКЕ “ОБРАЗОВАНИЕ ПРОСТЫХ АНАЛОГИИ”
1. Теленок 2. Лечение 3. Шелуха 4. Мясо 5. Лето 6. Жевать 7. Чешуя 8. Тонуть 9 Соль 10. Палец 11. Шуба 12. Слепой 13. Дерево 14. Паутина 15. Осень 16. Дом.
МЕТОДИКА “ЛОГИЧНОСТЬ” [9]
Вы получили бланк с 20-ю заданиями. Каждое из заданий представляет собой умозаключение, состоящее из 2-х взаимосвязанных суждений и вытекающего из них вывода. Требуется определить, какие выводы правильные, а какие ошибочные.
БЛАНК ЗАДАНИЙ К МЕТОДИКЕ “ЛОГИЧНОСТЬ”
1. Все металлы проводят электричество. Ртуть – металл. Следовательно, ртуть проводит электричество.
2. Все арабы смуглы. Ахмед смугл. Следовательно, Ахмед – араб.
3. Некоторые капиталистические страны – члены НАТО. Япония – капиталистическая страна. Следовательно, Япония – член НАТО.
4. Все Герои России награждаются Золотой звездой Героя. Иванов награжден Золотой звездой Героя. Следовательно, Иванов – Герой России.
5. Все сочинения Пушкина нельзя прочесть за одну ночь. “Медный всадник” - сочинение Пушкина. Следовательно, “Медный всадник” нельзя прочесть за одну ночь.
6. Лица, занимающиеся мошенничеством, привлекаются к уголовной ответственности. Л. мошенничеством не занимался. Следовательно, Л. не привлечен к уголовной ответственности.
7. Все студенты высшей школы изучают логику. Смирнова изучает логику. Следовательно, Смирнова – слушатель высшей школы.
8. Некоторые студенты МГУ – бывшие военнослужащие. Петров – студент МГУ. Следовательно, Петров – бывший военнослужащий.
9. Все хлебопекарни г. Кирова выполнили дневной план производства. Хлебопекарня ЧП Сидорова не является хлебопекарней г. Кирова. Следовательно, хлебопекарня ЧП Сидорова не выполнила дневной план производства.
10.Некоторые работники 2-го управления – юристы. Фомин – юрист. Следовательно, он работник 2-го управления.
11.Все граждане России имеют право на труд. Иванов – гражданин России. Следовательно, Иванов имеет право на труд.
12.Все металлы куются. Золото – металл. Следовательно, золото куется.
13.Все коренные жители Конго – негры. Мухаммед – негр. Следовательно, Мухаммед – житель Конго.
14.Все студенты Ленинградского университета изучают историю России. Н. Изучает историю России. Следовательно, Н. – студент Ленинградского университета.
15.Когда идет дождь, крыши домов мокрые. Крыши домов мокрые. Следовательно, идет дождь.
16.Некоторые капиталисты стремятся к развязыванию войны. Рассел – капиталист. Следовательно, Рассел стремится к развязыванию войны.
17.Все студенты 3-го курса написали курсовые работы по специальности. В. написал курсовую работу по специальности. Следовательно, В. – студент 3-го курса.
18.Комитет солдатских матерей выступает против войны. Джонс выступает против войны. Следовательно, Джонс входит в комитет солдатских матерей.
19.Некоторые капиталистические страны входят в состав Общего рынка. Австрия – капиталистическая страна. Следовательно, Австрия входит в состав Общего рынка.
20.Все ученики 3 “б” класса отличники. Петя Смирнов – отличник. Следовательно, Петя Смирнов – ученик 3 “б” класса.
КЛЮЧ К МЕТОДИКЕ “ЛОГИЧНОСТЬ”
Ответы “верно”: 1,11,12.
Ответы “неверно”: все остальные.
МЕТОДИКА “ИСКЛЮЧЕНИЕ ПОНЯТИЙ” [9]
Вы получили бланк, на котором написаны серии слов. Каждая серия состоит из пяти слов. Четыре из них являются в некоторой степени однородными понятиями и могут быть объединены по общему для них признаку, а одно слово не соответствует этим требованиям и должно быть исключено. Вы должны просмотреть каждую серию, найти слово, подлежащее исключению и выписать его на листочке под соответствующим номером. Например, даны пять слов: “кирпич, глина, известь, камень, дом”. Первые четыре слова можно объединить одном понятием “строительные материалы”, а последнее слово лишнее. Нужно записать “1.дом”. И так по порядку нужно решить все 17 серий.
БЛАНК ЗАДАНИЙ К МЕТОДИКЕ “ИСКЛЮЧЕНИЕ ПОНЯТИЙ”
1. дряхлый, старый, изношенный, маленький, ветхий
2. смелый, храбрый, отважный, злой, решительный
3. Василий, Федор, Семен, Иванов, Порфирий
3. молоко, сливки, сыр, сало, сметана
4. скоро, быстро, поспешно, постепенно, торопливо
5. глубокий, высокий, светлый, низкий, мелкий
6. лист, почка, кора, дерево, сук
7. дом, сарай, изба, хижина, здание
8. береза, сосна, дерево, дуб, ель
9. ненавидеть, презирать, негодовать, возмущаться, наказывать
10. темный, светлый, голубой, яркий, тусклый
11. гнездо, нора, курятник, берлога, сторожка
12. неудача, крах, провал, поражение, волнение
13. молоток, клещи, топор, гвоздь, долото
14. минута, секунда, час, вечер, сутки
15. грабеж, кража, землетрясение, поджог, нападение
16. успех, победа, удача, спокойствие, выигрыш.
КЛЮЧ К МЕТОДИКЕ “ИСКЛЮЧЕНИЕ ПОНЯТИЙ”
| 1. маленький | 2. злой | 3. Иванов |
| 4. сало | 5. постепенно | 6. светлый |
| 7. дерево | 8. сарай | 9. дерево |
| 10. наказывать | 11. голубой | 12. сторожка |
| 13. волнение | 14. гвоздь | 15. вечер |
| 16. землетрясение | 17. спокойствие |
Приложение 6
Диагностирующая контрольная работа №1
1. Найти точку, равноудаленную от трех данных точек.
2. Построить треугольник по данному основанию, боковой стороне и высоте, опущенной на основание.
3. Построить треугольник по двум углам и медиане.
Диагностирующая контрольная работа №2
1. Даны 3 точки: А, В, С. Постройте точку Х, которая равноудалена от точек А и В и находится на данном расстоянии от точки С.
2. Построить параллелограмм, зная одну из сторон, опущенную на эту сторону высоту и одну из диагоналей.
3. Построить треугольник, зная отношение трех его сторон и биссектрису угла
Программа факультативного курса занятий для 8 класса по теме “Задачи на построение и методы их решения”
Программа рассчитана на 6 часов. Занятия проводятся по 1 часу.
Занятие №1
Тема: ГМТ. Метод ГМТ.
Тип: урок изучения нового материала
Цели:
1) образовательные: повторить ранее изученный геометрический материал по теме решение задач на построение, сформировать у учащихся понятие геометрического места точек, сформировать представление о методе ГМТ, научить применять метод ГМТ при решении задач на построение, сформировать четкое представление об этапах решения задач на построение;
2) воспитательные: воспитать умение проводить анализ, исследование задачи, умение видеть решение, формировать грамотность речи;
3) развивающие: развить умение применять метод ГМТ для других задач.
Этапы:
1. Организационный момент
2. Актуализация знаний
3. Изучение нового материала
4. Решение задач
5. Подведение итогов.
Ход факультативного занятия:
1. Организационный момент
Как вы уже поняли из анкеты, задачи на построение можно решать различными методами: методом геометрических мест точек, подобия, осевой симметрии, центральной симметрии, поворота, параллельного переноса, алгебраическим методом. Сегодня на уроке мы введем понятие ГМТ и рассмотрим в чем заключается метод ГМТ. Запишите тему урока: “ГМТ. Метод ГМТ”.
Похожие работы
... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...
... координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных изображений. Можно выделить следующие цели изучения метода координат в школьном курсе геометрии: - дать учащимся эффективный метод решения задач и доказательства ряда теорем; - показать на основе этого метода тесную связь алгебры и геометрии; - способствовать ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
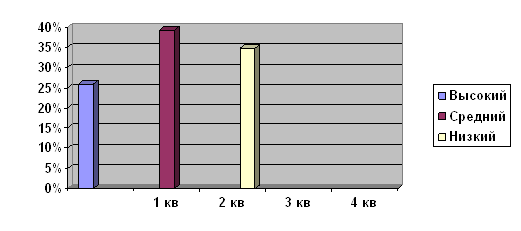
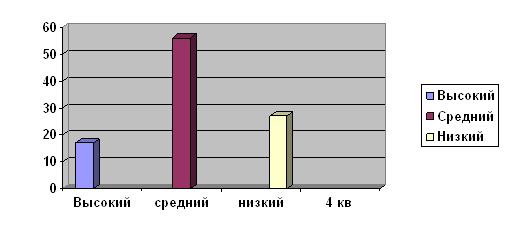
... Таким образом, в современном мире необходимы информационно-коммуникационные технологии. ГЛАВА II. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ ПО ТЕМЕ: «ИНФОРМАЦИОННО-КОММУНИКАЦИОННЫЕ ТЕХНОЛОГИИ КАК СРЕДСТВО РАЗВИТИЯ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА ПРИ ИЗУЧЕНИИ ЖИВОТНОГО МИРА В НАЧАЛЬНОЙ ШКОЛЕ» 2.1 Диагностика уровня развития познавательного интереса В результате изучения психолого-педагогической литературы ...

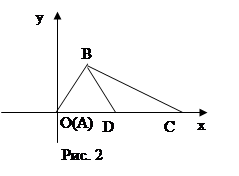
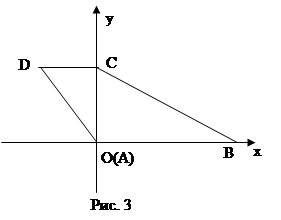





0 комментариев