Понятие пространственного мышления
Векторное пространство
Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА
А х в = в х а
Роль векторного пространства в формировании пространственного мышления учащихся основной школы
Методические аспекты развития пространственного мышления как элемента образного
Методика формирования пространственного мышления учащихся основной школы при изучении элементов геометрии
Методика формирования пространственного мышления учащихся основной школы при построении модели к задачам
Навигация
Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА
Формирование пространственного мышления при изучении векторного пространства у учащихся основной школы
83137
знаков
3
таблицы
3
изображения
1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.
2. а = ОА = ВС,
в = ОВ = АС, т.к. параллелограмм.
3. ОА + АС = ОВ + ВС = ОС, значит а + в = в + а. ч.т.д.
Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем: АВ + ВС =АС.
(а + в ) + с = (ОА + АВ) + ВС = ОВ + ВС = ОС,
а + (в + с ) = ОА + (АВ + ВС) = ОА + АС = ОС,
откуда и следует равенство
 | | ||||||||||
 | | ||||||||||
| | ||||||||||
а + ( в + с ) = (а + в) + с.
Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно (при некотором навыке) для решения задач при помощи векторов.
Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой «вектор», имеющий нулевую длину и не имеющий никакого направления; этот «вектор» изображается «отрезком нулевой длины», т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0.
Равенство векторов.
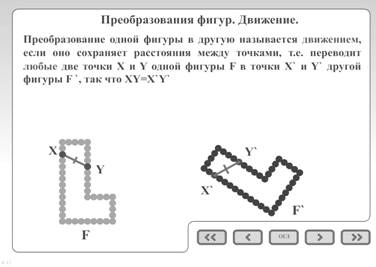
Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине.
И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.
Действительно, пусть векторы АВ и СD – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и СD равны, что и требовалось доказать.
Скалярное произведение двух векторов и его свойства.
Скалярным произведением двух нулевых векторов называется число, равное произведению числовых значений длин этих векторов на косинус угла между векторами.
Обозначение:
а х в = IaI * IbI * cos ( а, в).
Свойства скалярного произведения:
Похожие работы
... Остальные понятия, такие как сонаправленность полупрямых и равенство фигур, рекомендуется изучать классическим способом. Т.к. благодаря мультимедийному пособию ученикам уже известны основные свойства движений и они с помощью учителя без особых усилий смогут применить накопленные знания при изучении данных тем. Например, в теме «сонаправленность полупрямых» основным элементом является параллельный ...
... движение. Глава 3. развитие понятия функции в школьном курсе физике. §3.1. Функция как важнейшее звено межпредметных связей. В общей системе теоретических знаний учащихся по физике и математике в средней школе большое место занимает понятие «функция». Оно имеет познавательное и мировоззренческое значение и играет важную роль в реализации межпредметных связей [13]. Функция является одним ...
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
0 комментариев