Методические аспекты развития пространственного мышления как элемента образного

2.1 Методические аспекты развития пространственного мышления как элемента образного

Рассмотрим, какие подходы предлагают для развития пространственного мышления в средней школе и выясним возможности их использования.

А. Пардала выделяет такие основные типы упражнений, дидактическим назначением которых является формирование и развитие пространственных представлений учащихся: математические игры, связанные с пространственными представлениями; исследование конкретных геометрических объектов-фигур и преобразований; конструктивные задачи; прикладные задачи; проекционные стереометрические задачи; задачи на проектирование геометрических тел, построение сечений; диагностические задачи на проверку сформированности пространственных представлений.

Однако А. Я. Цукарь считает, что хотя это не классификация, тем не менее так смешивать (как это сделал А. Пардала) в одном перечне типы упражнений, одни из которых являются частным случаем других, а у некоторых совершенно разные основания, непозволительно. Очевидно, что выделять в отдельный тип диагностические задачи не имеет смысла. В математических играх могут использоваться самые разные задачи: и на проектирование, и на построение сечений. А разве задачи на проектирование геометрических тел не являются конструктивными? Налицо частая для методических публикаций нечётность в делении, как логической операции, иногда доходящая до эклектики.

Г. Н. Никитина говорит о методических приёмах развития пространственного мышления учащихся: привлечение неплоских пространственных образов при рассмотрении вопросов планиметрии; создание целостного геометрического образа с опорой на наглядность; создание ситуаций, способствующих активному оперированию геометрическим образом; творческое конструирование новых геометрических образов. В другой работе Г. Н. Никитина с авторам к показателям развития пространственного мышления относит умения: 1. создавать исходный геометрический образ, т. е. в графической модели передавать форму, размеры и взаимное расположение отдельных элементов объекта; 2. выбирать и произвольно изменять точку отсчёта; 3. сохранять в памяти геометрический образ; 4. анализировать и синтезировать геометрические образы; 5. рассматривать объект с разных точек зрения; 6. мысленно производить различные геометрические преобразования над исходным геометрическим образом; 7. мысленно изменять структуру геометрического образа; 8. осуществлять глазомерные оценки линейных и угловых величин. В приведённых выше делениях также имеется смешение разных оснований.

На каком-то этапе специалисты, образно говоря, занимаются "собирательством", чтобы затем более внимательно изучить и систематизировать накопленный материал. В последнее время появилось понимание того, что не только 5-6 классы среднего звена, а также и начальная школа, - благоприятное время для развития пространственного мышления. Поэтому хоть и медленно, но на уроке математики в начальных классах проникают специальные упражнения, направленные на его развитие. Затем в 6-9 классах эта проблема забывается и всплывает (по необходимости) в 10 классе, поскольку явно даёт о себе знать. Традиционно для развития пространственного воображения учеников 10-11 классов использовались задачи на построение сечений многогранников плоскостью. Эта тема находилась в центре внимания многих исследователей, начиная с Н. Ф. Четвертухина. Ей посвятил свою небольшую книгу К. С. Богушевский, которая помогла учителям увидеть место таких задач при изучении аксиом стереометрии и тем " Параллельность прямых и плоскостей ". Методистами разрабатывались системы задач, связанных с изображением пространственных фигур и с построением сечений многогранников плоскостью.

Основой формирования пространственного воображения является практическая работа ребёнка с пространственными объектами, манипулирование ими, изменение их положения в пространстве разъединение и соединение нескольких в один. Внешние действия субъекта с объектами являются необходимыми для того, чтобы он мог затем производить с ними внутренние, мысленные действия. Но они не являются достаточными. Любая деятельность воображения невозможна без фиксации её промежуточных этапов (конструкций) каким-либо простым способом (в знаково-символической форме). Поэтому для развития пространственного воображения школьников нужно вооружать их соответствующими знаниями о способах такой фиксации. Одним из самых распространенных является изображение пространственных объектов по принятым правилам. Необходимое условие формирования и развития пространственного воображения - наличие достаточно обширного и разнообразного материала для восприятия. Правильность, продуктивность его возрастает под влиянием упражнений, учитывающих всю гамму возможных операций над пространственными объектами, приводящих к созданию новых образов, ведь основная его функция - оперирование пространственными образами. Таким образом, явно выделяются два типа упражнений, лежащих в основе формирования и развития пространственного мышления : упражнения на умение читать изображения и изображать пространственные объекты, и упражнение на оперирование пространственными образами. В свою очередь, в них можно выделить разные виды: отыскание изображения из нескольких данных для предъявленного объекта; нахождение объекта из некоторого набора, соответствующего данному изображению; завершение изображения известного объекта по его фрагменту; идентификация различных изображений одного и того же пространственного объекта; узнавание фигуры по её проекциям; 6. определение взаимного расположения нескольких фигур по их изображениям; 7. оценивание формы и размеров фигуры; 8. построение проекций заданной фигуры; 9. построения изображения объекта по его 10. изображение объекта по его описанию; 11. изготовление модели по её чертежу, по предъявленному объекту, по его описанию; 12. узнавание и изображение объекта, полученного (мысленным) изменением ( с помощью поворота, симметрии, параллельного переноса) положения заданного; 13. узнавание и изображение фигуры, составленной из заданных по известному правилу; 14. изображение пересечения заданных фигур (в том числе после мысленного их перемещения); 15 изображение частей фигур после её мысленного расчленения.

Требования к содержанию (упражнениям) обучения, направленного на достижение необходимого уровня пространственного мышления (по Нурмагомедову). Упражнения должны строиться с расчётом: - использования конкретных представлений о материальных телах , их взаимном расположении в пространстве, об их свойствах (подвижность, неподвижность, устойчивость, неустойчивость, способность сохранения и изменения формы и т. п. ); учёта необходимости доминанты качественной оценки окружающих предметов над количественной, свойственной учащихся основной школы. Отсюда, например метрические представления не должны опережать представления о форме или взаимном расположении; обеспечения необходимой и обязательной работы по развитию речи, формированию активного словаря, характеризующего форму предметов и фигур, их свойств, отношения взаимного расположения в пространстве; - обеспечения использования при выполнении заданий и упражнений всех возможных рецепторов восприятия окружающего пространства (зрения, осязания, слуха). Отсюда необходимость обеспечения при решении упражнений разнообразных видов деятельности и способов решений.

Похожие работы

Использование мультимедийных средств при изучении основных свойств движений в курсе планиметрии основной школы

Скачать

82430

1

7

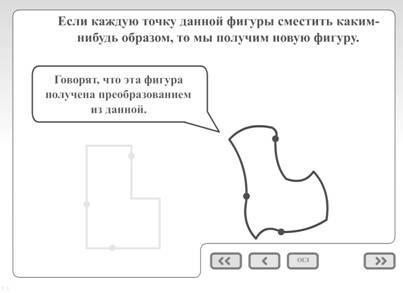
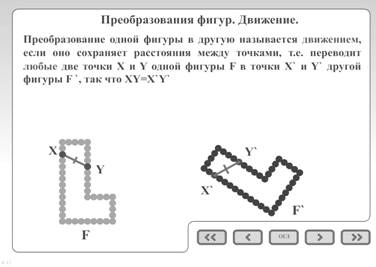
... Остальные понятия, такие как сонаправленность полупрямых и равенство фигур, рекомендуется изучать классическим способом. Т.к. благодаря мультимедийному пособию ученикам уже известны основные свойства движений и они с помощью учителя без особых усилий смогут применить накопленные знания при изучении данных тем. Например, в теме «сонаправленность полупрямых» основным элементом является параллельный ...

Математика и физика в средней школе

Скачать

41919

0

0

... движение. Глава 3. развитие понятия функции в школьном курсе физике. §3.1. Функция как важнейшее звено межпредметных связей. В общей системе теоретических знаний учащихся по физике и математике в средней школе большое место занимает понятие «функция». Оно имеет познавательное и мировоззренческое значение и играет важную роль в реализации межпредметных связей [13]. Функция является одним ...

Решение задач на построение в курсе геометрии основной школы как средство развития логического мышления школьников

Скачать

147329

8

14

... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9.   Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10.             Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...

Развитие логического мышления учащихся при решении задач на построение

Скачать

249522

15

58

... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...