Розвиток просторових уявлень молодших школярів
Наукові основи вивчення геометричного матеріалу у початкових класах
Методика вивчення геометричного матеріалу у початкових класах
Ознайомлення з геометричними фігурами та задачами на їх розпізнавання
Відстань між містами дорівнює 70 км. Зобразіть цю відстань відрізком у зошиті, припустивши, що 1 см становить 10 км
Слід практикувати обчислення площі прямокутних ділянок за і планом
Навигация
Методика вивчення геометричного матеріалу у початкових класах
Формування геометричних понять у молодших школярів
59323
знака
2
таблицы
1
изображение
2. Методика вивчення геометричного матеріалу у початкових класах
Головне спрямування геометричного матеріалу, визначеного програмою і реалізованого в системі ретельно дібраних задач, – сформувати достатньо повну систему геометричних уявлень (образи геометричних фігур, їх елементів, відношень між фігурами та їх елементами).
На цій основі формуються просторові уявлення й уява, розвивається мова й мислення учнів, а також організовується робота, спрямована на вироблення важливих практичних навичок.
Перед учителем постає важливе завдання дібрати методику розкриття змісту геометричного матеріалу на тому рівні, якого досягнуть учні на чає їх переходу до IV класу, а також визначите головні напрямки вивчення цього матеріалу.
Робота з формування геометричних уявлень має проводитися так: властивості фігур учні виявляють експериментально, одночасно засвоюють необхідну термінологію й дістають певні навички; головне місце в навчанні повинні посідати практичні роботи учнів, спостереження й робота з геометричними об'єктами.
Оперуючи різноманітними предметами, моделями геометричних фігур, розглядаючи їх у процесі численних дослідів, учні помічають найзагальніші їх ознаки (що не залежить від матеріалу, кольору, положення, маси і т.п.).
У методиці формування геометричних уявлень важливо іти від «речі» до фігури (до її образу), а також навпаки, – від образу до реальної речі.
Це досягається систематичним використанням прийому матеріалізації геометричних образів. Наприклад, пряму лінію не тільки креслимо за допомогою лінійки, уявлення про неї дає і край – ребро лінійки, натягнута нитка, лінія згину аркуша паперу, лінія перетину двох площин (наприклад, площин стіни і стелі). Абстрагуючись від конкретних властивостей матеріальних речей, учні оволодівають і геометричними уявленнями. Так, наприклад, можна видозмінювати спосіб ділення многокутника відрізком на частини.
У І класі в основному завершується початкове ознайомлення з фігурами і їх назвами. Цього досягають, розглядаючи навколишні предмети, готові моделі і зображення фігур. Діти поступово опановують схему вивчення фігур, їх аналізу і синтезу, що полегшує засвоєння властивостей кожної фігури.
Чільне місце в методиці відводиться прийому зіставлення і протиставлення геометричних фігур. У І класі це дає змогу з множини фігур наочно (без визначень) виділяти множини відповідно кругів, многокутників, ліній і т.д.; у II и III класах уточнювати властивості фігур, класифікувати їх, Волика увага приділяється протиставленню і зіставленню плоских фігур (круг – многокутник, коло – круг і т.д.); плоских і просторових фігур (квадрат – куб; круг – куля та ін.).
Причому ця робота має відбуватися не тільки на уроках математики, а й па уроках трудового навчання й особливо – малювання, коли відтворення форми предмета залежить від якості й глибини аналізу його геометричної форми. Наприклад, розглядаючи куб (або предмет, який мас форму куба), треба знайти в ньому характерні точки, відрізки, многокутники, під час розгляду кулі можна звернути увагу на її круглі перерізи.
Уже в процесі початкового ознайомлення з геометричними фігурами в І класі діти виконують розумові операції аналізу й синтезу. Важливим завданням учителя, яке визначає методику навчання на цьому етапі, є аналіз фігури, на основі чого виділяються її істотні властивості (ознаки) і неістотні. Так, істотним для трикутника є не його положення на площині (аркуші паперу), не відносні розміри сторін, а їх кількість – три сторони (кути, вершини); для прямокутника істотним є те, що він чотирикутник (чотири кути) і всі його кути – прямі. Все інше не істотне.
У процесі навчання виникає потреба застосування геометричної і логічної термінології, символіки, креслень. Так, уже II класі введення буквеної символіки допомагає не тільки розрізняти фігури та їх елементи, а й є одним Із засобів формування умінь узагальнювати. Наприклад, із запису ОК < 5 см діти довідуються, що відрізок ОК – будь-який, але має довжину, меншу за 5 см.
З досвіду навчання математики в І–III класах відомо, що діти легко і з інтересом сприймають не тільки очевидні прості, а й складні геометричні факти; під впливом цього учитель починає недооцінювати наочний і практичний підхід до вивчення геометричного матеріалу, не виконує мінімуму вправ, вміщених у підручнику, мало звертає уваги на прищеплення учням практичних навичок. Такий учитель стає на неправильний і небезпечний шлях формального ознайомлення молодших школярів з геометричними фігурами: не за допомогою спостережень, виготовлення з паперу і креслення, а повідомляючи формальне означення, тобто лише словесним способом.
В І–III класах такі поняття, як «відрізок», «многокутник», «кут» і т. п., неозначувані. Та вже в IV класі вони означаються. Із сказаного випливає, що молодших школярів немає сенсу запитувати: «Що називається (що таке) відрізком? Що називається многокутником? Що називається кутом?» і т.п., оскільки відповідні поняття тут не означаються, але їм уже можна ставити запитання: «що називається трикутником (чотирикутником, п'ятикутником)?» і т.п. Діти мають відповідати на це, приміром, так; «Трикутник – це многокутник, у якого три кути (вершини, сторони)». Тут можна давати дещо надмірне означення прямокутника як чотирикутника, у якого всі кути прямі. Спроби завчасної формалізації ознайомлення молодших школярів з геометричними фігурами спричиняють завищення програмних вимог, недостатнє, а іноді, й неправильне засвоєння матеріалу. Наприклад, у класах, де вчителі зловживали «теоретичним» підходом до вивчення фігур, багато учнів не змогли правильно показати всі фігури, зображені на мал. 10. Вони плутали відрізок (2) і пряму (14), чотирикутник (8) і замкнуту ламану лінію (9).
Як правило, вищого рівня засвоєння матеріалу досягають ті вчителі, які, розуміючи самостійне значення геометричних знань, намагаються пов'язувати вивчення геометричного матеріалу з іншими питаннями початкового курсу математики. Такий зв'язок ґрунтується на можливості встановлення відношень між числом і фігурою, властивостями чисел і фігур. Це дає змогу використати фігури в процесі формування поняття числа, властивостей чисел, операцій над ними і, навпаки, використати числа для вивчення властивостей геометричних образів та їх відношень.
У І класі фігури слід застосовувати як об'єкти для лічби поряд з іншими предметами. Трохи згодом такими об'єктами мають стати елементи фігур, наприклад вершини, сторони, кути многокутників. Учні поступово ознайомлюються з вимірюванням відрізків. Це дає змогу встановлювати зв'язок між відрізками і числами. У II класі безпосередній зв'язок установлюється між відрізками (точками) і числами. Геометричні фігури використовуються під час ознайомлення учнів з частинами. У всіх зазначених випадках відкриваються широкі можливості органічно пов'язати вивчення геометричних об'єктів з арифметичним матеріалом, що входить у курс математики для І–III класів.
Уже в І–III класах здійснюються найпростіші класифікації кутів (прямі і непрямі), многокутників (за числом кутів) і т.д. Вивчення родових і видових понять підготовляє дітей до розуміння означень, в яких такі відмінності зазначатимуться.
Запровадження вправ, де діти позначають (виділяють) точки, які належать або не належать фігурі чи кільком фігурам, створює можливість надалі трактувати геометричну фігуру як множину точок. А це дає змогу більш свідомо виконувати операції поділу фігури на частини або побудови фігури з інших (складання), тобто виконувати, по суті, операції об'єднання, перерізу, доповнення над точковими множинами.
Важливою загальною методичною лінією зв'язку у вивченні геометричного матеріалу з рештою питань курсу початкової математики є, таким чином, неявна опора на теоретико-множинні і найпростіші логіко-математичні уявлення у вивченні фігур, їх відношень, властивостей.
Учитель має систематично проводити роботу з формування в учнів умінь і навичок застосовувати креслярські й вимірювальні інструменти, зображувати геометричні фігури, пояснювати процеси й результати праці, застосовувати символіку і термінологію. Важливою методичною умовою реалізації цієї системи є спочатку свідоме виконання дій і лише згодом автоматизація цих дій.
В результаті навчання в І–III класах в учнів слід сформувати початкові уявлення про точність побудов і вимірювань.
У І класі діти оволодівають навичками вимірювання і побудови відрізків за допомогою лінійки (з точністю до 1 см). При цьому ставляться не менші вимоги, ніж це звичайно робиться, скажімо, під час прищеплення учням навичок письма.
У II–III класах для вимірювань й побудов поступово запроваджуються нові інструменти: циркуль, циркуль-вимірювач, косинець, рулетка. Підвищуються вимоги щодо точності цих операцій, а також якості креслень і моделей, які виготовляють діти, та записів ходу й результатів викопаної роботи.
Роботу з формування навичок треба проводити поступово, розподіляючи її рівномірно майже на кожному уроці (і не тільки з математики). Це створює умови для частішого застосування цих навичок у навчальній і практичній діяльності, забезпечує необхідну їх стійкість.
Для правильного визначення методики навчання молодших школярів учителю треба мати загальні уявлення про систему завдань підручників. Ця система охоплює в кожному класі задачі:
а) у яких геометричні фігури використовуються як об'єкти для перелічування (круги, многокутники, їх елементи). При розв'язуванні таких задач учні здебільшого засвоюють необхідну термінологію і набувають уміння розпізнавати фігури;
б) пов'язані з формуванням уявлень про геометричні величини (довжину, площу) і навичок вимірювання відрізків, площ фігур;
в) обчислювальні, в яких треба знаходити периметр многокутників, площу прямокутника;
г) на елементарні побудови геометричних фігур на папері в клітинку, на нелінійованому папері за допомогою лінійки, косинця, циркуля (без урахування розмірів);
д) на елементарні побудови фігур із заданими параметрами (трикутник прямим кутом, прямокутник з даними сторонами і т.д.);
е) на класифікацію фігур;
є) на ділення фігур на частини (в тому числі на рівні частини) і на складання фігур з інших;
ж) пов'язані з прищепленням основних навичок читання геометричних креслень, використанням буквених позначень (формуванням «геометричної зіркості»);
з) на з'ясування геометричної форми предметів або їх частин. [2, 69]
Похожие работы
... культури учнів початкових класів, поглибити розуміння дітьми взаємозв’язків у природі, взаємозалежності між її об’єктами та явищами. Однією з педагогічних умов ефективного формування екологічної культури молодших школярів є цілеспрямоване та системне планування уроків, виховних заходів з використанням екологічно спрямованого матеріалу, зв’язок його з життям, що забезпечує підпорядкованість всієї ...
... . 2.2 Формування наукового світогляду молодших школярів в процесі застосування засобів художньо-творчої діяльності в навчально-виховному процесі Метою формуючого експерименту ми визначили формування світогляду молодших школярів засобами художньо-творчої діяльності. Формуючий експеримент здійснювався протягом 5 тижнів з використанням системи різноманітних засобів (див. додаток Б, В, Г, Є, ...
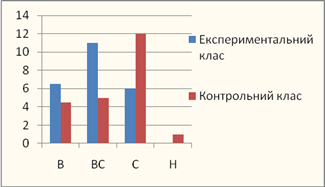
... порівняно з контрольним значно підвищився рівень розвитку графічних умінь. Це свідчить про ефективність застосовуваного напрямку роботи. 2.3 Обґрунтування ефективних шляхів і засобів формування графічних умінь у молодших школярів на уроках трудового навчання Перед сучасною школою стоїть складне і відповідальне завдання — формування особистості, здатної самостійно оволодівати знаннями і вміти ...
... галицького побутового костюма на спеціалізованих уроках образотворчого мистецтва у 3 класі (див. додатки Б-В). Вирішальним для учнів початкових класів в плані формування художньо-конструктивного мислення молодших школярів засобами галицького побутового костюма були зміст і якість проведення уроків образотворчого мистецтва. В результаті впровадження в систему занять з образотворчого мистецтва ...
0 комментариев