Ознайомлення з геометричними фігурами та задачами на їх розпізнавання

2.1 Ознайомлення з геометричними фігурами та задачами на їх розпізнавання

Геометричні поняття доцільно вводити описово, конструктивно. Наприклад, кутом можна називати фігуру, утворену двома променями, що мають спільний початок, і кут, вирізаний із листка паперу, а також кут трикутника, кут прямокутника, тобто потрібно пов'язувати це поняття з життєвим досвідом. Це ж можна сказати про два відрізки однакової довжини, що збігаються при накладанні.

Вже в першому класі на уроках математики знайомимо дітей із геометричними фігурами: точка, лінія пряма, ламана, коло, квадрат, трикутник тощо. А на уроці образотворчого мистецтва дітям роздаються аркуші, на кожному з яких намальовано коло. Пропонуємо домалювати коло так, щоб вийшов знайомий предмет. Малюнки у всіх вийшли різні: футбольний м’яч, обличчя клоуна, яблуко, вишня, курчатко, кавун, Чебурашка, торт тощо. Такі завдання треба поступово ускладнювати: дітям дається не один аркуш із формою кола (або іншою геометричною фігурою), а скільки вони забажають; нові геометричні форми: півколо, прямокутник, овал, ромб тощо.

Художники розглядали геометричні фігури з точки зору естетики, тому, що навіть звичайні з них (точка, лінія, трикутник тощо) при повторенні утворюють декоративний ефект. Здавна витвори декоративно-прикладного мистецтва прикрашали різними орнаментами. Оскільки кожна геометрична фігура – це закінчена форма, вона вже може служити модулем для конструювання геометричного орнаменту.

На уроках математики та праці доцільно використовувати різні дидактичні ігри з геометричними фігурами.

Наприклад:

Гра «Архітектор»: з кружечків, прямокутників і трикутників склади аплікації різних тварин.

Домалюй будинок, розфарбуй його.

Поряд намалюй ще одну рибку, але так, щоб вона пливла в інший бік.

У грі «Як тут було?» учням пропонується листівка, розрізана на частини. Треба відновити попередню картинку, складаючи ці частини.

У казковому місті «Круги» все кругле. Спробуй із різних кружечків скласти будиночок для ляльки, автомашину тощо.

Важливо ще з перших днів навчання у школі на різних уроках вчити дітей бачити геометричні фігури серед навколишніх предметів.

Завдання. Озирнись навколо себе. Серед звичайних предметів заховалося чимало різних геометричних фігур, тільки треба навчитися їх бачити. Пильно розглянь кожен предмет і спробуй знайти геометричну фігуру, на яку він схожий. Уважно розглянь наш клас, речі, що лежать у тебе в портфелі: книжка, пенал, олівець, лінійка, гумка. У деяких предметах заховалася лише одна геометрична фігура, але в тебе в портфелі є багато предметів, у яких заховалося одразу кілька фігур (гумка – 6 прямокутників). Коли діти шукають предмети, схожі на геометричні фігури, у них з’являються дуже цікаві приклади.

Завдання. З яких геометричних фігур складається казкове місто? Використовуючи знайомі тобі фігури, домалюй його так, як тобі подобається. Розфарбуй казковий палац. Обґрунтуй свій вибір.

Навіть учням молодших класів не дуже цікаво невідомо навіщо розфарбовувати геометричні фігури. Щоб зацікавити їх, можна розповісти казку, де головними героями будуть фігури. Під час розповіді діти пробують конструювати так, як герої казки, розмірковують, уявляють ситуації.

У другому класі за Програмою розпочинається знайомство з об’ємними геометричними формами. Вчитель демонструє їх на уроках математики, дає цікаві завдання. Незвичайні для дітей ситуації розвивають уяву, логічність та нестандартність мислення. У наступних завданнях дітям необхідно придумати, як доступним способом можна змінити предмет, щоб у ньому з’явилися нові геометричні фігури.

Формування уявлень про пряму, криву, відрізок прямої

Так, у математиці в початкових класах, під час вивчення початкового курсу геометрії, що закладає основи планіметрії, чітко прослідковуються чотири основні лінії:

1) первісні (неозначувані) поняття – точка, пряма, площина, лежати, лежати між, лежати по один бік, довжина відрізка, градусна міра кута;

2) перші означення – відрізок, рівні відрізки, кут, рівні кути, трикутник, рівні трикутники, півпряма, паралельні прямі;

3) аксіоми планіметрії;

4) перші доведення.

Формування поняття про пряму і криву лінії можна почати показом спочатку обвислого, а потім натягнутого тонкого шнура. Учням варто запропонувати зігнути аркуш паперу довільної форми і в будь-якому напрямі. Розправивши цей аркуш, вони побачать, що на ньому утворилася пряма лінія. Тут можна сказати, що пряма лінія нескінченна, а бачимо ми лише її частину.

Навчаючи дітей проводити прямі лінії за допомогою лінійки, вчитель спочатку демонструє виконання такої роботи на аркуші білого паперу, прикріпленого до класної дошки. Учні мають навчитися будувати вертикальну, горизонтальну і похилу прямі.

Введення відрізка передує першим вправам на вимірювання довжини. Вчитель креслить на дошці пряму лінію і позначає на ній рисками дві точки. Він пояснює дітям, що частину прямої, обмежену двома точками, називають відрізком прямої або відрізком. Кінці відрізка на малюнку позначають тоненькими рисочками або точками. Якщо на малюнку рисочок (точок) немає, то це зображення прямої.

Так, означення відрізка поділяється на такі логічні частини: відрізком називається // частина прямої, // яка складається з усіх точок цієї прямої, // що лежать між двома даними її точками // – кінцями відрізка.

Після ознайомлення з поняттям відрізка дітей вчать порівнювати їх за довжиною. Спочатку відрізки порівнюють «на око». При цьому вживають слова «рівні», «нерівні», «однакові», «довший», «коротший». Потім порівнюють за довжиною дві палички (дві смужки), прикладаючи їх одна до одної.

У 1 класі вони ознайомлюються з мірами 1 см і 1 дм. Учні 2 класу оволодівають навичками побудови відрізків заданої довжини, розв'язування задач на знаходження довжини ламаної, обчислення периметра прямокутника. Вводиться нова одиниця вимірювання довжини метр.

У 3 класі вводять буквене позначення відрізків. Відрізки широко використовуються для розгляду понять збільшення і зменшення числа в кілька разів, кратного порівняння чисел та ін. У 4 класі вимірювання і креслення відрізків здебільшого пов'язані з розв'язуванням задач, зокрема задач на знаходження відстаней та на знаходження дробу від числа.

Креслення відрізків за масштабом. Як правило, такі завдання учні виконують під безпосереднім керівництвом учителя. Пояснення ведеться під час виконання вправ виду:

1. Довжина накресленого на дошці відрізка АО дорівнює 8 дм. Побудуйте в зошиті зображення цього відрізка у зменшеному вигляді, припустивши, що 1 см відрізка в зошиті означатиме 1 дм відрізка на дошці.

Скільки сантиметрів становить довжина накресленого в зошиті відрізка? У скільки разів відрізок на дошці довший, ніж відрізок, накреслений у зошиті?

2. Відстань між містами дорівнює 70 км. Зобразіть цю відстань відрізком у зошиті, припустивши, що 1 см становить 10 км.

Наведемо приклади завдань, в яких використовується поняття масштабу:

1. Відстань між двома населеними пунктами зображено відрізком КМ. Обчисліть цю відстань, взявши до уваги, що в 1 см вміщується 5 км.

2. Знайдіть відстані між Києвом та Вінницею і Києвом та Житомиром. Порівняйте відстані. Масштаб: в І см – 20 км.

Формування уявлень про ламану

Подається окрема ламана лінія і ставиться запитання: зі скількох відрізків складено ламану лінію?

У 3 класі вводять буквене позначення відрізків. Відрізки широко використовуються для розгляду понять збільшення і зменшення числа в кілька разів, кратного порівняння чисел та ін.

У 4 класі вимірювання і креслення відрізків здебільшого пов'язані з розв'язуванням задач, зокрема задач на знаходження відстаней та на знаходження дробу від числа.

Креслення відрізків за масштабом. Як правило, такі завдання учні виконують під безпосереднім керівництвом учителя. Пояснення ведеться під час виконання вправ виду:

1. Довжина накресленого на дошці відрізка АО дорівнює 8 дм. Побудуйте в зошиті зображення цього відрізка у зменшеному вигляді, припустивши, що 1 см відрізка в зошиті означатиме 1 дм відрізка на дошці.

Скільки сантиметрів становить довжина накресленого в зошиті відрізка? У скільки разів відрізок на дошці довший, ніж відрізок, накреслений у зошиті?

Похожие работы

Формування екологічної культури молодших школярів

Скачать

93477

3

2

... культури учнів початкових класів, поглибити розуміння дітьми взаємозв’язків у природі, взаємозалежності між її об’єктами та явищами. Однією з педагогічних умов ефективного формування екологічної культури молодших школярів є цілеспрямоване та системне планування уроків, виховних заходів з використанням екологічно спрямованого матеріалу, зв’язок його з життям, що забезпечує підпорядкованість всієї ...

Формування світогляду молодших школярів

Скачать

120541

8

5

... .   2.2 Формування наукового світогляду молодших школярів в процесі застосування засобів художньо-творчої діяльності в навчально-виховному процесі Метою формуючого експерименту ми визначили формування світогляду молодших школярів засобами художньо-творчої діяльності. Формуючий експеримент здійснювався протягом 5 тижнів з використанням системи різноманітних засобів (див. додаток Б, В, Г, Є, ...

Формування графічних умінь молодших школярів на уроках трудового навчання

Скачать

92444

1

8

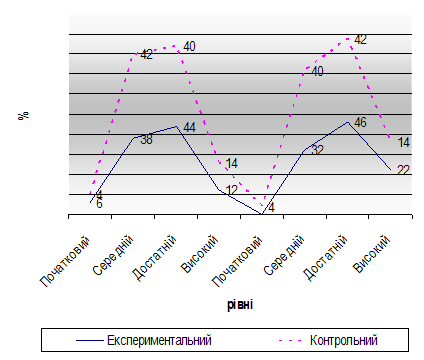
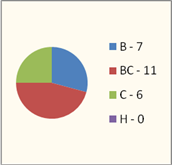
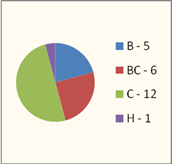
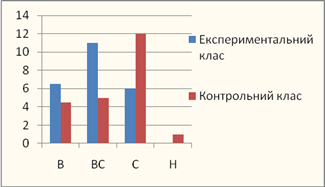
... порівняно з контрольним значно підвищився рівень розвитку графічних умінь. Це свідчить про ефективність застосовуваного напрямку роботи. 2.3 Обґрунтування ефективних шляхів і засобів формування графічних умінь у молодших школярів на уроках трудового навчання Перед сучасною школою стоїть складне і відповідальне завдання — формування особистості, здатної самостійно оволодівати знаннями і вміти ...

Формування художньо-конструктивного мислення у молодших школярів

Скачать

153128

0

13

... галицького побутового костюма на спеціалізованих уроках образотворчого мистецтва у 3 класі (див. додатки Б-В). Вирішальним для учнів початкових класів в плані формування художньо-конструктивного мислення молодших школярів засобами галицького побутового костюма були зміст і якість проведення уроків образотворчого мистецтва. В результаті впровадження в систему занять з образотворчого мистецтва ...