Навигация
Искусственное начальное решение
20533
знака
10
таблиц
1
изображение
4.2.3. Искусственное начальное решение
Для получения начального базисного решения мы использовали остаточные переменные. Однако когда исходное ограничение записано в виде равенства или имеет знак, нельзя сразу же получить НДБР. Поэтому были разработаны два метода, в которых используется «штрафование» искусственных переменных.
1. Метод больших штрафов (М-метод)
Рассмотрим линейную модель, приведённую к стандартной форме:
минимизировать
при ограничениях
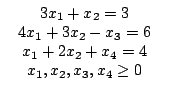
В первом и втором уравнениях нет переменных, исполняющих роль остаточных. Поэтому введём в каждое из этих уравнений по одной из искусственных переменных R1 и R2: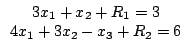 
За использование этих переменных в составе целевой функции можно ввести штраф, приписывая им достаточно большой положительный коэфффициент 
. Получим линейную модель:
минимизировать
при ограничениях
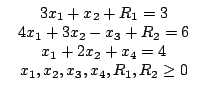
Теперь если
,то начальное допустимое решение: 
Метод оптимизации, направленный на нахождение минимального значения 
, приведёт к тому, что переменные R1 и R2 в оптимальном решении обратятся в нуль.
Необходимо переформулировать условие задачи, чтобы представить процесс решения в удобной табличной форме. Подставив в целевую функцию полученные из соответствующих ограничений выражения для искусственных переменных
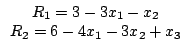
получим выражение для :
Решение представлено в сводной таблице:
| Итерация |
|
|
|
|
|
| Решение | Отношение | |
|
|
|
|
|
|
|
|
| - | |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| - | |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| - | |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| - | |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| - | |
|
|
|
|
|
|
|
|
| - | |
|
|
|
|
|
|
|
|
| - | |
|
|
|
|
|
|
|
|
| - |
2. Т.к. целевая функция минимизируется, переменные, включаемые в базис, должны иметь наибольшие положительные коэффициенты в -уравнении. Оптимум достигается, когда все небазисные переменные имеют коэффициенты в -уравнении. Оптимальному решению соответствует точка 
.
Т.к. в оптимальном решении отсутствуют искусственные переменные, имеющие положительное значение, то данное решение – допустимое оптимальное решение задачи в её стандартной постановке.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...
0 комментариев