Двойственность

Ограничения на допустимое множество Графическое решение задачи ЛП Представление пространства решений стандартной задачи ЛП Искусственное начальное решение Двухэтапный метод Двойственность

20533

знака

таблиц

изображение

Двухэтапный метод

5. Двойственность.

Двойственная задача – вспомогательная задача ЛП, формулируемая с помощью определённых правил непосредственно из исходной, или прямой задачи.

Прямая задача ЛП в стандартной форме:

максимизировать (минимизировать)

$z=\sum \nolimits _{j=1}^{n}c_{j}x_{j}$

при ограничениях

$\sum \nolimits _{j=1}^{n}a_{ij}x_{j}=b_{i},\, i=\overline{1,m},\, j=\overline{1,n},\, x_{j}\ge 0$

В состав включаются избыточные и остаточные переменные.

$x_{1}$	$x_{2}$	$\ldots$	$x_{j}$	$\ldots$	$x_{n}$
$c_{1}$	$c_{2}$	$\ldots$	$c_{j}$	$\ldots$	$c_{n}$
$a_{11}$	$a_{12}$	$\ldots$	$a_{1j}$	$\ldots$	$a_{1n}$	$b_{1}$	$y_{1}$
$a_{21}$	$a_{22}$	$\ldots$	$a_{2j}$	$\ldots$	$a_{2n}$	$b_{2}$	$y_{2}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$a_{m1}$	$a_{m2}$	$\ldots$	$a_{mj}$	$\ldots$	$a_{mn}$	$b_{m}$	$y_{m}$

Для формулировки двойственной задачи расположим коэффициенты прямой задачи согласно схеме:

· каждому ограничению прямой задачи соответствует переменная двойственной задачи;

· каждому переменной прямой задачи соответствует ограничение двойственной задачи;

· коэффициенты при некоторой переменной, фигурирующие в ограничения прямой задачи, становятся коэффициентами левой части соответствующего ограничения двойственной задачи, а коэффициент, фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становится постоянной правой части этого же ограничения двойственной задачи.

Информация о других условиях двойственной задачи (направление оптимизации, ограничения и знаки двойственных переменных) представлена в таблице:

Прямая задача в стандартной форме.	Двойственная задача
Целевая функция	Целевая функция	Ограничения	Переменные
Максимизация	Минимизация	$\ge$	Не ограничены в знаке
Минимизация	Максимизация	$\le$	Не ограничены в знаке

Рассмотрим пример:

Прямая задача:

максимизировать

$z=5x_{1}+12x_{2}+4x_{3}$

при ограничениях

$\begin{displaymath}\begin{array}{c}x_{1}+2x_{2}+x_{3}\le 10\\2x_{1}-x_{2}+3x_{3}=8\\x_{1},x_{2},x_{3}\ge 0\end{array}\end{displaymath}$

Прямая задача в стандартной форме:

максимизировать

$z=5x_{1}+12x_{2}+4x_{3}+0x_{4}$

при ограничениях

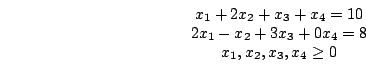
$\begin{displaymath}\begin{array}{c}x_{1}+2x_{2}+x_{3}+x_{4}=10\\2x_{1}-x_{2}+3x_{3}+0x_{4}=8\\x_{1},x_{2},x_{3},x_{4}\ge 0\end{array}\end{displaymath}$

Двойственная задача:

минимизировать

$\omega =10y_{1}+8y_{2}$

при ограничениях:

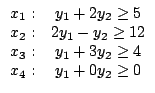
$\begin{array}{cc}x_{1}: & y_{1}+2y_{2}\ge 5\\x_{2}: & 2y_{1}-y_{2}\ge 12\\x_{3}: & y_{1}+3y_{2}\ge 4\\x_{4}: & y_{1}+0y_{2}\ge 0\end{array}$

(означает, что y1>0). y1, y2 не ограничены в знаке.

Двухэтапный метод

Раздел: Информатика, программирование
Количество знаков с пробелами: 20533
Количество таблиц: 10
Количество изображений: 1

Скачать

... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...

Скачать

... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...

Скачать

... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...

Скачать

... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями