Навигация
3. Двухэтапный метод
Этап 1. Вводятся искусственные переменные, необходимые для получения стартовой точки. Записывается новая целевая функция, предусматривающая минимизацию суммы искусственных переменных при исходных ограничениях, видоизменённых за счёт искусственных переменных. Если минимальное значение новой целевой функции равно нулю (т.е. все искусственные переменные в оптимуме равны нулю), то исходная задача имеет допустимое решение и переходим к Этапу 2.
Этап 2. Оптимальное базисное решение, полученное на Этапе 1, используется в качестве начального условия исходной задачи.
Рассмотрим на примере.
Этап 1.
Минимизация
![]()
при ограничениях
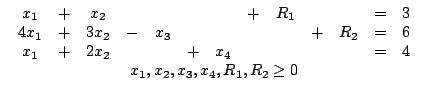
![]()
|
|
|
|
|
|
| Решение | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.к. ![]() , можно переходить к Этапу 2.
, можно переходить к Этапу 2.
Этап 2. Исходную задачу сформулируем следующим образом:
минимизировать
![]()
при ограничениях
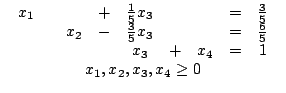
Теперь, приравняв x3=0, получим НДБР
![]()
Для решения задачи необходимо подставить в целевую функцию выражения для базисных переменных x1 и x2:
![]()
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...





0 комментариев