Навигация
Оценка параметров распределения случайных величин для четырех законов
1.3 Оценка параметров распределения случайных величин для четырех законов
В выражениях для плотности и функции нормального распределения (4 – 5) параметры m и s являются математическим ожиданием и среднеквадратичным отклонением. Поэтому, если мы остановились на нормальном распределении, то берем их равными, соответственно, выборочным математическому ожиданию и среднеквадратичному отклонению:
![]() . (12)
. (12)
Математическое ожидание показательного распределения есть величина, обратная его параметру a. Поэтому, если мы выбрали показательное распределение, параметр a находим:
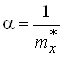 (13)
(13)
Из выражений для mx и sx равномерного закона распределения находим его параметры a и b:
![]() ;
; ![]() . (14)
. (14)
Параметр s рэлеевского распределения также находится из выражения для mx
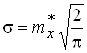 (15)
(15)
В системе MATLAB вычисление параметров теоретического распределения с помощью ПМП реализовано в функциях fit или mle. Подбор по методу моментов не реализован. Найдем параметры теоретического распределения по ПМП и методу моментов.
Практическая часть.
s={'нормальное распределение'; 'показательное распределение';…
'равномерное распределение'; 'Рэлеевское распределение'};
disp ('Параметры по ПМП:')
[mx, sx]=normfit(x);% параметры нормального распределения
lam=1/expfit(x);% параметр показательного распределения
[a, b]=unifit(x);% параметры равномерного распределения
sig=raylfit(x);% параметр Рэлеевского распределения
fprintf([' % s: m=%12.7f; sigma=%12.7f\n'], s{1}, mx, sx)
fprintf (' % s: alpha=%12.7f\n', s{2}, lam)
fprintf (' % s: a=%12.7f; b=%12.7f\n', s{3}, a, b)
fprintf (' % s: sigma=%12.7f\n', s{4}, sig)
Для сигнала гусеничной техники:
Параметры по ПМП:
нормальное распределение: m= 0.0060038; sigma= 0.0203706
показательное распределение: alpha= 166.5608494
равномерное распределение: a= -0.0962308; b= 0.0942564
Рэлеевское распределение: sigma= 0.0150166
Для фонового сигнала:
Параметры по ПМП:
нормальное распределение: m= 0.0188599; sigma= 0.0005663
показательное распределение: alpha= 53.0224920
равномерное распределение: a= 0.0106122; b= 0.0210241
Рэлеевское распределение: sigma= 0.0133420
disp ('Параметры по методу моментов:')
mx=Mx;
sx=Sx;% параметры нормального распределения
lam=abs (1/Mx);% параметр показательного распределения
a=Mx-Sx*3^0.5;
b=Mx+Sx*3^0.5;% параметры равномерного распределения
sig=abs(Mx)*(2/pi)^0.5;% параметр Рэлеевского распределения
fprintf([' % s: m=%12.7f; sigma=%12.7f\n'], s{1}, mx, sx)
fprintf (' % s: alpha=%12.7f\n', s{2}, lam)
fprintf (' % s: a=%12.7f; b=%12.7f\n', s{3}, a, b)
fprintf (' % s: sigma=%12.7f\n', s{4}, sig)
Для сигнала гусеничной техники:
Параметры по методу моментов:
нормальное распределение: m= 0.0060038; sigma= 0.0203706
показательное распределение: alpha= 166.5608494
равномерное распределение: a= -0.0292791; b= 0.0412867
Рэлеевское распределение: sigma= 0.0047903
Для фонового сигнала:
Параметры по методу моментов:
нормальное распределение: m= 0.0188599; sigma= 0.0005663
показательное распределение: alpha= 53.0224920
равномерное распределение: a= 0.0178790; b= 0.0198409
Рэлеевское распределение: sigma= 0.0150480
Вывод: из результатов, полученных двумя методами видно, что оценки плотностей распределения вероятностей для равномерного и рэлеевского законов по первому методу отличаются от плотностей распределения вероятностей по второму методу.
Оценки показательных и нормальных законов плотностей распределения вероятностей по обоим методам практически совпадают.
1.4 Построение на одном графике теоретического и практического распределения для формулировки гипотезы
Построим на одном графике теоретическую и эмпирическую плотности распределения вероятности. Эмпирическая плотность распределения – это гистограмма, у которой масштаб по оси ординат изменен таким образом, чтобы площадь под кривой стала равна единице. Для этого все значения в интервалах необходимо разделить на nh, где n – объем выборки, h – ширина интервала при построении гистограммы. Теоретическую плотность распределения вероятности строим по одному из выражений (4), (6), (8), (10), параметры для них уже вычислены. Эмпирическую плотность распределения нарисуем красной линией, а предполагаемую теоретическую – линией одного из цветов: синего, зеленого, сиреневого или черного.
Практическая часть.
[nj, xm]=hist (x, k);% число попаданий и середины интервалов
delta=xm(2) – xm(1);% ширина интервала
clear xfv fv xft ft% очистили массивы для f(x)
xfv=[xm-delta/2; xm+delta/2];% абсциссы для эмпирической f(x)
xfv=reshape (xfv, prod (size(xfv)), 1);% преобразовали в столбец
xfv=[xl; xfv(1); xfv; xfv(end); xr];% добавили крайние
fv=nj/(n*delta);% значения эмпирической f(x) в виде 1 строки
fv=[fv; fv];% 2 строки
fv=[0; 0; reshape (fv, prod (size(fv)), 1); 0; 0];% + крайние, 1 столбец
xft=linspace (xl, xr, 1000)';% абсциссы для теоретической f(x)
ft=[normpdf (xft, mx, sx), exppdf (xft, 1/lam),…
unifpdf (xft, a, b), raylpdf (xft, sig)];
col='bgmk';% цвета для построения графиков
figure
plot (xfv, fv, '-r', xft, ft(:, 1), col(1), xft, ft(:, 2), col(2),…
xft, ft(:, 3), col(3), xft, ft(:, 4), col(4)) % рисуем
set (get(gcf, 'CurrentAxes'),…
'FontName', 'Times New Roman Cyr', 'FontSize', 12)
title ('\bfПлотности распределения')
xlim([xl xr]), ylim([0 1.4*max(fv)])% границы рисунка по осям
xlabel ('\itx')% метка оси x
ylabel ('\itf\rm (\itx\rm)')% метка оси y
grid
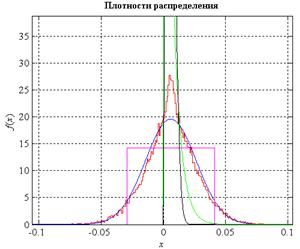
Рис. 9 – График плотности распределения вероятности сигнала гусеничной техники и графики нормального, рэлеевского, показательного и равномерного законов плотностей распределения вероятности
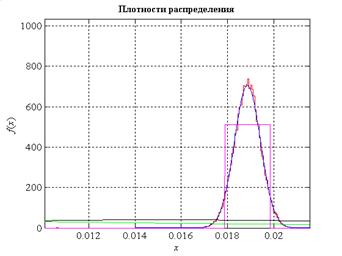
Рис. 10 – График плотности распределения вероятности фонового сигнала и графики нормального, рэлеевского, показательного и равномерного законов плотностей распределения вероятности
Вывод: из рисунка 9 видно, что наиболее подходящим теоретическим распределением для первой эмпирической гистограммы является нормальное.
Реальный закон распределения амплитуд фонового сигнала также подчиняется нормальному закону.
Похожие работы
... установкой антивирусных средств на рабочие станции пользователей. Это сложная задача, требующая комплексного подхода к решению. Одно из главных преимуществ данного решения - рассмотрение подсистемы защиты информации от вредоносных программ как многоуровневой системы. Первый уровень включает в себя средства защиты от вредоносных программ, устанавливаемые на стыке с глобальными сетями (Интернет ...
... заболевания в результате паралича дыхания. 4. Зажигательное оружие Важное место в системе обычных вооружений принадлежит зажигательному оружию, которое представляет собой комплекс средств поражения , основан- ных на использовании зажигательных веществ. По американской классификации, зажигательное оружие относится к оружию массового поражения. Учитывается также способность зажигательного ...
... . 5. Получены длительные непрерывные ряды наблюдений интенсивности потока и азимутальных распределений СДВ атмосфериков, которые позволили проследить динамику грозовой активности в мировых грозовых центрах. 5.1. Морской мониторинг показал, что основной вклад в мировую грозовую активность дают континентальные и островные грозовые центры. Вариации интенсивности потока импульсов хорошо ...
... сигнал на когерентность, исключает случайные, побочные результаты измерений без потери чувствительности частотомера. Анализаторы спектра Этот уже достаточно развитый, но еще перспективный вид средств радиоконтроля предназначен для сканирования частотных спектров модулированных сигналов в различных частотных диапазонах и отображения на экране дисплея/осциллографа этих спектров. В случае, ...


0 комментариев