Проверка гипотезы по критерию Колмогорова-Смирнова

1.5 Проверка гипотезы по критерию Колмогорова-Смирнова

Мы подобрали вид теоретического распределения и его параметры. Следующий этап – это проверка правильности подбора. Необходимо выяснить: насколько хорошо теоретическое распределение согласуется с данными. С этой целью используются критерии согласия Колмогорова-Смирнова или Пирсона., во втором – f(x) и f^*(x).

Критерий согласия Колмогорова. В этом случае сравниваются теоретическая F(x) и выборочная F^*(x) функции распределения. Сравниваемым параметром является максимальная по модулю разность между двумя функциями

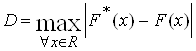. (16)

С точки зрения выборочного метода F^*(x) является случайной функцией, так как от выборки к выборке ее вид меняется, поэтому величина D является случайной. Согласно теореме Гливенко-Кантелли с ростом объема выборки эта величина сходится к нулю. Колмогоров А.Н. выяснил, как именно D сходится к нулю. Он рассмотрел случайную величину

 (17)

и нашел ее закон распределения. Как оказалось, при достаточно больших n он вообще не зависит от закона распределения генеральной совокупности X. Причем функция распределения случайной величины L имеет вид

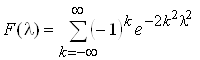. (18)

Если опытные данные x действительно взяты из генеральной совокупности с функцией распределения F(x), то вычисленная по выражению (18) реализация l случайной величины L на уровне значимости q должна лежать в квантильных границах распределения Колмогорова (18). При этом, если l малое (выходит за «левый» квантиль), то нулевая гипотеза принимается: теоретическое распределение согласуется с опытными данными. В общем случае нулевая гипотеза принимается, если выполняется условие

l £ l_1-q. (19)

Данный критерий называется еще критерием Колмогорова-Смирнова.

Таким образом, для применения критерия согласия Колмогорова-Смирнова, мы должны найти максимальную по модулю разность между выборочной и теоретической функциями распределения D по выражению (16), вычислить по ней l и проверить условие (19).

Практическая часть.

param=[[mx sx]; [lam 0]; [a b]; [sig 0]];% параметры распределений

qq=[];% критические уровни значимости

for idistr=1:ndistr, % критерий Колмогорова

[hkolm, pkolm, kskolm, cvkolm]=…

kstest (x, [x cdf (tdistr{idistr}, x,…

param (idistr, 1), param (idistr, 2))], 0. 1,0);

qq=[qq pkolm];% критические уровни значимости

end

[maxqq, bdistr]=max(qq);% выбрали лучшее распределение

fprintf(['Лучше всего подходит % s;\nкритический уровень '…

'значимости для него =%8.5f\n'], s{bdistr}, maxqq);

figure

cdfplot(x);% эмпирическая функция распределения

xpl=linspace (xl, xr, 500);% для графика F(x)

ypl=cdf (tdistr{bdistr}, xpl, param (bdistr, 1), param (bdistr, 2));

hold on% для рисования на этом же графике

plot (xpl, ypl, 'r');% дорисовали F(x)

hold off

set (get(gcf, 'CurrentAxes'),…

'FontName', 'Times New Roman Cyr', 'FontSize', 12)

title(['\bfПодобрано ' s{bdistr}])

xlabel ('\itx')% метка оси x

ylabel ('\itf\rm (\itx\rm)')% метка оси y

Результат:

Лучше всего подходит нормальное распределение;

критический уровень значимости для него = 0.31369

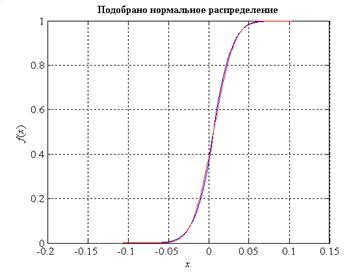
Рис. 11 – График эмпирической функции распределения для сигнала гусеничной техники

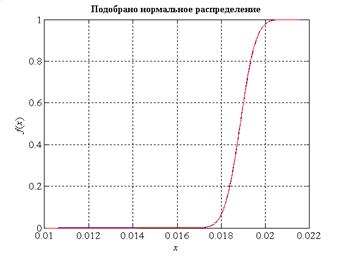
Рис. 12 – График эмпирической функции распределения для фонового сигнала

Найденный критический уровень значимости – это то значение q, при котором неравенство (19) обращается в равенство.

Вывод: По полученным результатам можно сделать вывод, что по данному критерию распределение подобранно верно.

 

1.6 Проверка гипотезы по критерию согласия Пирсона

По критерию Пирсона сравниваются теоретическая и эмпирическая функции плотности распределения вероятности, а точнее – частота попадания случайной величины в интервал. Интервалы могут быть любыми, равными и неравными, но удобно использовать те интервалы, на которых построена гистограмма. Эмпирические числа попадания n (из гистограммы) сравнивается с теоретическим np_j, где p_j – вероятность попадания случайной величины X в j-ый интервал:

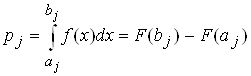, (20)

a_j и b_j – границы j-го интервала. Карл Пирсон показал, что, если все np_j ³ 5, то суммарная квадратическая относительная разность между теоретическим и практическим числом попаданий в интервал равна

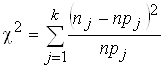 (21)

имеет приближенно c² распределение Пирсона с k – m степенями свободы, где m – число параметров, оцениваемых по выборке, плюс 1. Так как параметров два, то m = 3. Выражение (21) представляет собой статистику Пирсона.

Теоретическое распределение можно считать подобранным верно, если выполняется условие

. (22)

Построим таблицу результатов, в которую занесем: номера интервалов (1-й столбец), границы интервалов a_j и b_j (2-й и 3-й столбцы), вероятность попадания в интервал p_j (4-й столбец), теоретическое число попаданий и практическое число попаданий np_j (6-й столбец). Границы интервалов и практическое число попаданий взяты из гистограммы, теоретическая вероятность попадания в j-й интервал подсчитывается по выражению (20).

Практическая часть.

clear Tabl% очистили таблицу результатов

Tabl(:, 1)=[1:k]';% номера интервалов

Tabl(:, 2)=xm'-delta/2;% левые границы интервалов

Tabl(:, 3)=xm'+delta/2;% правые границы интервалов

Tabl (1,2)=-inf;% теоретическое начало 1-го интервала

Tabl (k, 3)=inf;% теоретический конец последнего интервала

Tabl(:, 4)=nj';% опытные числа попаданий

bor=[Tabl(:, 2); Tabl (end, 3)];% все границы интервалов

pro=cdf (tdistr{bdistr}, bor, param (bdistr, 1), param (bdistr, 2));

Tabl(:, 5)=pro (2:end) – pro (1:end-1);% вероятности попаданиz pj

Tabl(:, 6)=n*Tabl(:, 5);% теоретическое число попаданий npj

disp ('Сводная таблица результатов')

fprintf (' j aj bj')

fprintf (' nj pj npj\n')

fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f\n', Tabl')

Для сигнала гусеничной техники:

Сводная таблица результатов

j aj bj nj pj npj

1 – Inf -0.09544 2 0.00000 0.01837

2 -0.09544 -0.09464 2 0.00000 0.00408

3 -0.09464 -0.09385 0 0.00000 0.00495

4 -0.09385 -0.09306 1 0.00000 0.00599

5 -0.09306 -0.09226 1 0.00000 0.00724

6 -0.09226 -0.09147 0 0.00000 0.00873

7 -0.09147 -0.09067 0 0.00000 0.01052

8 -0.09067 -0.08988 4 0.00000 0.01266

9 -0.08988 -0.08909 0 0.00000 0.01520

10 -0.08909 -0.08829 0 0.00000 0.01824

11 -0.08829 -0.08750 2 0.00000 0.02184

12 -0.08750 -0.08671 2 0.00000 0.02612

13 -0.08671 -0.08591 0 0.00000 0.03118

14 -0.08591 -0.08512 3 0.00000 0.03718

15 -0.08512 -0.08433 1 0.00000 0.04425

Для фонового сигнала:

Сводная таблица результатов

j aj bj nj pj npj

1 – Inf 0.01067 1 0.00000 0.00000

2 0.01067 0.01074 0 0.00000 0.00000

3 0.01074 0.01080 0 0.00000 0.00000

4 0.01080 0.01086 0 0.00000 0.00000

5 0.01086 0.01092 0 0.00000 0.00000

6 0.01092 0.01098 0 0.00000 0.00000

7 0.01098 0.01104 0 0.00000 0.00000

8 0.01104 0.01111 0 0.00000 0.00000

9 0.01111 0.01117 0 0.00000 0.00000

10 0.01117 0.01123 0 0.00000 0.00000

11 0.01123 0.01129 0 0.00000 0.00000

12 0.01129 0.01135 0 0.00000 0.00000

13 0.01135 0.01141 0 0.00000 0.00000

14 0.01141 0.01147 0 0.00000 0.00000

15 0.01147 0.01154 0 0.00000 0.00000

Если распределение подобрано, верно, то числа из 4-го и 6-го столбцов не должны сильно отличаться.

Вывод: Для сигнала гусеничной техники числа из 4-го и 6-го столбцов значительно отличаются, значит, распределение подобрано неверно. А для фонового сигнала эти числа практически совпадают.

Проверим выполнение условия np_j ³ 5 и объединим те интервалы, в которых np_j< 5. Перестроим таблицу и добавим в нее еще один, 7-й столбец – слагаемое, вычисляемое по выражению (21).

Практическая часть.

qz=0.3;% выбрали уровень значимости

ResTabl=Tabl (1,1:6);% взяли первую строку

for k1=2:k, % берем остальные строки таблицы

if ResTabl (end, 6)<5, % предыдущее npj<5 – будем суммировать

ResTabl (end, 3)=Tabl (k1,3);% новая правая граница интервала

ResTabl (end, 4:6)=ResTabl (end, 4:6)+Tabl (k1,4:6);% суммируем

else% предыдущее npj>=5 – будем дописывать строку

ResTabl=[ResTabl; Tabl (k1,1:6)];% дописываем строку

end

end

if ResTabl (end, 6)<5, % последнее npj<5

ResTabl (end – 1,3)=ResTabl (end, 3);% новая правая граница

ResTabl (end – 1,4:6)=ResTabl (end – 1,4:6)+ResTabl (end, 4:6);

ResTabl=ResTabl (1:end-1,:);% отбросили последнюю строку

end

kn=size (ResTabl, 1);% число объединенных интервалов

ResTabl(:, 1)=[1:kn]';% новые номера интервалов

ResTabl(:, 7)=(ResTabl(:, 4) – ResTabl(:, 6)).^2./ResTabl(:, 6);

disp ('Сгруппированная сводная таблица результатов')

fprintf (' j aj bj')

fprintf (' nj pj npj ')

fprintf([' (nj-npj)^2/npj\n'])

fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f % 12.5f\n', ResTabl')

hi2=sum (ResTabl(:, 7));% сумма элементов последнего столбца

fprintf(['Статистика Пирсона chi2=%10.5f\n'], hi2)

m=[3,2,3,2];% число ограничений

fprintf ('Задаем уровень значимости q=%5.4f\n', qz)

chi2qz=chi2inv (1-qz, kn-m(bdistr));% квантиль

fprintf(['Квантиль chi2-распределения Пирсона '…

'chi2 (1-q)=%10.5f\n'], chi2qz)

if hi2<=chi2qz,

disp ('Распределение подобрано верно, т. к. chi2<=chi2 (1-q)')

else

disp ('Распределение подобрано неверно, т. к. chi2>chi2 (1-q)')

end

Для сигнала гусеничной техники:

Сгруппированная сводная таблица результатов

j aj bj nj pj npj (nj-npj)^2/npj

1 – Inf -0.07004 58 0.00009 5.46033 505.53988

2 -0.07004 -0.06607 32 0.00011 6.16617 108.23348

3 -0.06607 -0.06369 17 0.00011 6.35867 17.80845

4 -0.06369 -0.06210 16 0.00010 5.89961 17.29233

5 -0.06210 -0.06051 16 0.00013 7.65444 9.09908

6 -0.06051 -0.05893 16 0.00017 9.87115 3.80530

7 -0.05893 -0.05813 9 0.00010 5.93889 1.57781

8 -0.05813 -0.05734 16 0.00012 6.71391 12.84370

9 -0.05734 -0.05655 12 0.00013 7.57856 2.57953

10 -0.05655 -0.05575 17 0.00015 8.54160 8.37603

11 -0.05575 -0.05496 15 0.00017 9.61240 3.01967

12 -0.05496 -0.05416 17 0.00019 10.80104 3.55773

13 -0.05416 -0.05337 13 0.00021 12.11825 0.06416

14 -0.05337 -0.05258 26 0.00024 13.57548 11.37115

15 -0.05258 -0.05178 20 0.00026 15.18487 1.52688

Статистика Пирсона chi2=2613.15423

Задаем уровень значимости q=0.3000

Квантиль chi2-распределения Пирсона chi2 (1-q)= 182.25040

Распределение подобрано неверно, т. к. chi2>chi2 (1-q)

Вывод: По критерию Пирсона распределение подобрано неверно, т. к. реальное значение статистики χ²_р=2613.15423 намного превышает критическое значение χ²_т,f=182.25040, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала не подтверждается на уровне значимости 0.05.

Для фонового сигнала:

Сгруппированная сводная таблица результатов

j aj bj nj pj npj (nj-npj)^2/npj

1 – Inf 0.01690 11 0.00026 7.51515 1.61596

2 0.01690 0.01702 13 0.00031 8.99732 1.78070

3 0.01702 0.01708 14 0.00026 7.55999 5.48594

4 0.01708 0.01714 15 0.00037 10.63561 1.79095

5 0.01714 0.01720 13 0.00052 14.78664 0.21588

6 0.01720 0.01727 24 0.00071 20.31617 0.66797

7 0.01727 0.01733 33 0.00097 27.58544 1.06279

8 0.01733 0.01739 35 0.00130 37.01551 0.10975

9 0.01739 0.01745 54 0.00172 49.08550 0.49205

10 0.01745 0.01751 58 0.00225 64.32627 0.62217

11 0.01751 0.01757 79 0.00291 83.30848 0.22282

12 0.01757 0.01764 102 0.00373 106.62418 0.20055

13 0.01764 0.01770 137 0.00472 134.86147 0.03391

14 0.01770 0.01776 167 0.00590 168.57212 0.01466

15 0.01776 0.01782 185 0.00729 208.23287 2.59213

Статистика Пирсона chi2= 57.37478

Задаем уровень значимости q=0.3000

Квантиль chi2-распределения Пирсона chi2 (1-q)= 66.27446

Распределение подобрано, верно, т. к. chi2<=chi2 (1-q)

Вывод: Для фонового сигнала по критерию Пирсона распределение подобрано верно, т. к. реальное значение статистики χ²_р=609411.53699 не превышает критическое значение χ²_т,f=520.15366, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала подтверждается.