Обучение нейронной сети

4. Обучение нейронной сети.

 

4.1 Общие сведения о нейронных сетях

Искусственные НС представляет собой модели, в основе которых лежат современные представления о строении мозга человека и происходящих в нем процессах обработки информации. ИНС уже нашли широкое применение в задачах: сжатия информации, оптимизации, распознавание образов, построение экспертных систем, обработки сигналов и изображений и т.д.

Связь между биологическим и искусственным нейронами

 

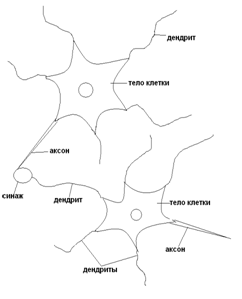
Рисунок 20 – Структура биологического нейрона

Нервная система человека состоит из огромного количества связанных между собой нейронов, порядка 10¹¹; количество связей исчисляется числом 10¹⁵.

Представим схематично пару биологических нейронов (рисунок 20).Нейрон имеет несколько входных отростков – дендриты, и один выходной – аксон. Дендриты принимают информацию от других нейронов, аксон – передает. Область соединения аксона с дендритом (область контакта) называется синапсом. Сигналы, принятые синапсами, подводятся к телу нейрона, где они суммируются. При этом, одна часть входных сигналов являются возбуждающими, а другая – тормозящими.

Когда входное воздействие превысит некоторый порог, нейрон переходит в активное состояние и посылает по аксону сигнал другим нейронам.

Искусственный нейрон – это математическая модель биологического нейрона (Рисунок 21). Обозначим входной сигнал через х, а множество входных сигналов через вектор X = {х1, х2, …, хN}. Выходной сигнал нейрона будем обозначать через y.

Изобразим функциональную схему нейрона.

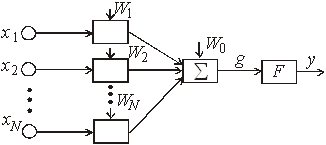
Рисунок 21 – Искусственный нейрон

Для обозначения возбуждающего или тормозящего воздействия входа, введем коэффициенты w₁, w₁, …, w_N – на каждый вход, то есть вектор

W = {w₁, w₁, …, w_N}, w₀ – величина порога. Взвешенные на векторе W входные воздействия Х перемножаются с соответствующим коэффициентом w, суммируются и формируется сигнал g:

 

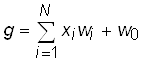
Выходной сигнал является некоторой функцией от g

,

где F – функция активации. Она может быть различного вида:

1)         ступенчатой пороговой

2)        

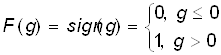
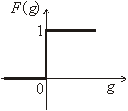 или

 

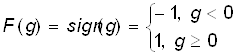
В общем случае:

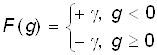
2) линейной, которая равносильна отсутствию порогового элемента вообще

F(g) = g

3) кусочно-линейной, получаемая из линейной путем ограничения диапазона её изменения в пределах , то есть

 

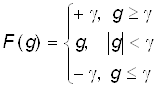
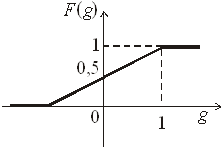
4) сигмоидальной

 

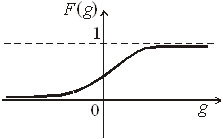
5) многопороговой

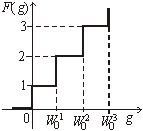
6) гиперболический тангенс

F(g) = tanh(g)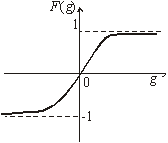

Чаще всего входные значения преобразуются к диапазону XÎ [0, 1]. При w_i = 1 (i = 1, 2,…, N) нейрон является мажоритарным элементом. Порог в этом случае принимает значение w₀ = N/2.

Еще один вариант условного изображения искусственного нейрона приведен на рисунке 22

Рисунок 22 – Условное обозначение искусственного нейрона

С геометрической точки зрения, нейрон при линейной функции активации описывает уравнение линии, если на входе одно значение x₁

 

или плоскости, когда на входе вектор значений Х

 

Структура (архитектура, топология) нейронных сетей

Существует множество способов организации ИНС, в зависимости от: числа слоев, формы и направления связей.

Изобразим пример организации нейронных сетей (рисунок 23).

 

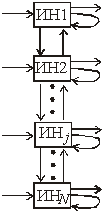
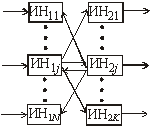
Однослойная структура Двухслойная структура с обратными связями с обратными связями

 

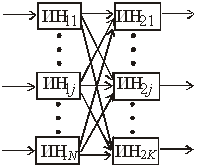
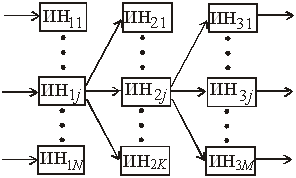
Двухслойная структура Трехслойная структура с прямыми связями с прямыми связями

Рисунок 23 – Примеры структур нейронных сетей

На рисунке 24 изображена трехслойная НС с прямыми связями. Слой нейронов, непосредственно принимающий информацию из внешней среды, называется входным слоем, а слой, передающий информацию во внешнюю среду – выходным. Любой слой, лежащий между ними и не имеющий контакта с внешней средой, называется промежуточным (скрытным) слоем. Слоев может быть и больше. В многослойных сетях, как правило, нейроны одного слоя имеют функцию активации одного типа.

Рисунок 24 – Трехслойная нейронная сеть

При конструировании сети в качестве исходных данных выступают:

– размерность вектора входного сигнала, то есть количество входов;

– размерность вектора выходного сигнала. Число нейронов в выходном слое, как правило, равно числу классов;

– формулировка решаемой задачи;

–    точность решения задачи.

Например, при решении задачи обнаружения полезного сигнала НС может иметь один или два выхода.

Создание или синтез НС – это задача, которая в настоящее время теоретически не решена. Она носит частный характер.

Обучение нейронных сетей

Одним из самых замечательных свойств нейронных сетей является их способность обучаться. Несмотря на то, что процесс обучения НС отличается от обучения человека в привычном нам смысле, в конце такого обучения достигаются похожие результаты. Цель обучения НС заключается в её настройке на заданное поведение.

Наиболее распространенным подходом в обучении нейронных сетей является коннекционизм. Он предусматривает обучение сети путем настройки значений весовых коэффициентов wij, соответствующих различным связям между нейронами. Матрица W весовых коэффициентов wij сети называется синаптической картой. Здесь индекс i – это порядковый номер нейрона, из которого исходит связь, то есть предыдущего слоя, а j – номер нейрона последующего слоя.

Существует два вида обучения НС: обучение с учителем и обучение без учителя.

Обучение с учителем заключается в предъявлении сети последовательности обучаемых пар (примеров) (Хi, Hi), i = 1, 2, …, m образов, которая называется обучающей последовательностью. При этом для каждого входного образа Хi вычисляется реакция сети Y_iи сравнивается с соответствующим целевым образом H_i. Полученное рассогласование используется алгоритмом обучения для корректировки синаптической карты таким образом, чтобы уменьшить ошибку рассогласования. Такая адаптация производится путем циклического предъявления обучающей выборки до тех пор, пока ошибка рассогласования не достигнет достаточно низкого уровня.

Хотя процесс обучения с учителем понятен и широко используется во многих приложениях нейронных сетей, он всё же не полностью соответствует реальным процессам, происходящим в мозге человека в процессе обучения. При обучении наш мозг не использует какие-либо образы, а сам осуществляет обобщение поступающей извне информации.

В случае обучения без учителя обучающая последовательность состоит лишь из входных образов Хi. Алгоритм обучения настраивает веса так, чтобы близким входным векторам соответствовали одинаковые выходные векторы, то есть фактически осуществляет разбиение пространства входных образов на классы. При этом до обучения невозможно предсказать, какие именно выходные образы будут соответствовать классам входных образов. Установить такое соответствие и дать ему интерпретацию можно лишь после обучения.

Обучение НС можно рассматривать как непрерывный или как дискретный процесс. В соответствии с этим алгоритмы обучения могут быть описаны либо дифференциальными уравнениями, либо конечно-разностными. В первом случае НС реализуется на аналоговой, во втором – на цифровых элементах. Мы будем говорить только о конечно-разностных алгоритмах.

Фактически НС представляет собой специализированный параллельный процессор или программу, эмулирующую нейронную сеть на последовательной ЭВМ.

Большинство алгоритмов обучения (АО) НС выросло из концепции Хэбба. Он предложил простой алгоритм без учителя, в котором значение веса w_ij, соответствующее связи между i-м и j-м нейронами, возрастает, если оба нейрона находятся в возбужденном состоянии. Другими словами, в процессе обучения происходит коррекция связей между нейронами в соответствии со степенью корреляции их состояний. Это можно выразить в виде следующего конечно-разностного уравнения:

,

где w_ij(t + 1) и w_ij (t) – значения веса связей нейрона i с нейроном j до настройки (на шаге t+1) и после настройки (на шаге t) соответственно; v_i (t) – выход нейрона i и выход нейрона j на шаге t; v_j (t) – выход нейрона j на шаге t; α – параметр скорости обучения.

Стратегия обучения нейронных сетей

Наряду с алгоритмом обучения не менее важным является стратегия обучения сети.

Одним из подходов является последовательное обучение сети на серии примеров (Х_i, H_i) i = 1, 2, …, m, составляющих обучающую выборку. При этом сеть обучают правильно реагировать сначала на первый образ Х₁, затем на второй Х₂ и т.д. Однако, в данной стратегии возникает опасность утраты сетью ранее приобретенных навыков при обучении каждому следующему примеру, то есть сеть может «забыть» ранее предъявленные примеры. Чтобы этого не происходило, надо сеть обучать сразу всем примерам обучающей выборки.

Х₁ ={Х₁₁,…, Х_1N} можно обучать 100 ц 1

Х₂ = {Х₂₁,…, Х_2N} 100 ц 2 100 ц

……………………

Х_m = {Х_m1,…, Х_mN} 100 ц 3

Так как решение задачи обучения сопряжено с большими сложностями, альтернативой является минимизация целевой функции вида:

,

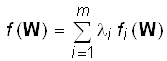где l_i – параметры, определяющие требования к качеству обучения нейронной сети по каждому из примеров, такие, что λ₁ + λ₂ + … + λ_m = 1.

Практическая часть.

Сформируем обучающее множество:

P_o=cat (1, Mt, Mf);

P_o=P_o';

Зададим структуру нейронной сети для задачи обнаружения:

net = newff (minmax(P_o), [npr 2], {'logsig', 'logsig'}, 'trainlm', 'learngdm');

net.trainParam.epochs = 100;% заданное количество циклов обучения

net.trainParam.show = 5;% количество циклов для показа промежуточных результатов;

net.trainParam.min_grad = 0;% целевое значение градиента

net.trainParam.max_fail = 5;% максимально допустимая кратность превышения ошибки проверочной выборки по сравнению с достигнутым минимальным значением;

net.trainParam.searchFcn = 'srchcha';% имя используемого одномерного алгоритма оптимизации

net.trainParam.goal = 0;% целевая ошибка обучения

Функция newff предназначена для создания «классической» многослойной нейронной сети с обучением по методу обратного распространения ошибки. Данная функция содержит несколько аргументов. Первый аргумент функции – это матрица минимальных и максимальных значений обучающего множества Р_о, которая определяется с помощью выражения minmax (P_o).

Вторые аргументы функции, задаются в квадратных скобках и определяют количество и размер слоев. Выражение [npr 2] означает, что нейронная сеть имеет 2 слоя. В первом слое – npr=10 нейронов, а во втором – 2. Количество нейронов в первом слое определяется размерностью входной матрицы признаков. В зависимости от количества признаков в первом слое может быть: 5, 7, 12 нейронов. Размерность второго слоя (выходной слой) определяется решаемой задачей. В задачах обнаружения полезного сигнала на фоне микросейсма, классификации по первому и второму классам, на выходе нейронной сети задается 2 нейрона.

Третьи аргументы функции определяют вид функции активации в каждом слое. Выражение {'logsig', 'logsig'} означает, что в каждом слое используется сигмоидально-логистическая функция активации , область значений которой – (0, 1).

Четвертый аргумент задает вид функции обучения нейронной сети. В примере задана функция обучения, использующая алгоритм оптимизации Левенберга-Марквардта – 'trainlm'.

Первые половина векторов матрицы Т инициализируются значениями {1, 0}, а последующие – {0, 1}.

net=newff (minmax(P_o), [10 2], {'logsig', 'logsig'}, 'trainlm', 'learngdm');

net.trainParam.epochs = 1000;

net.trainParam.show = 5;

net.trainParam.min_grad = 0;

net.trainParam.max_fail = 5;

net.trainParam.searchFcn = 'srchcha';

net.trainParam.goal = 0;

Программа инициализации желаемых выходов нейронной сети Т:

n1=length (Mt(:, 1));

n2=length (Mf(:, 1));

T1=zeros (2, n1);

T2=zeros (2, n2);

T1 (1,:)=1;

T2 (2,:)=1;

T=cat (2, T1, T2);

Обучение нейросети:

net = train (net, P_o, T);

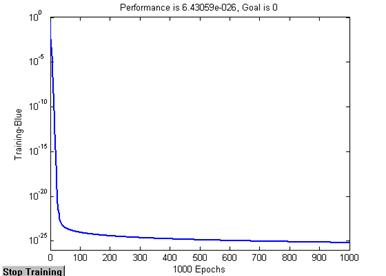
Рисунок 25 – График обучения нейронной сети.

Произведем контроль нейросети:

P_k=[Mt; Mf];

P_k=P_k';

Y_k=sim (net, P_k);

Команда sim передает данные из контрольного множества P_k на вход нейронной сети net, при этом результаты записываются в матрицу выходов Y_k. Количество строк в матрицах P_k и Y_k совпадает.

Pb=sum (round(Y_k (1,1:100)))/100

Оценка вероятности правильного обнаружения гусеничной техники Pb=1 alpha = sum (round(Y_k (1,110:157)))/110

Оценка вероятности ложной тревоги alpha =0

Определяем среднеквадратическую ошибку контроля с помощью желаемых и реальных выходов нейронной сети Еk.

[Ek] = T-Y_k;

sqe_k = mse(Ek)

Величина среднеквадратической ошибки контроля составляет:

sqe_k = 2.5919e-026

Протестируем работу нейросети. Для этого сформируем матрицу признаков тестового сигнала:

h3=tr_t50-mean (tr_t50);

Mh1=MATRPRIZP (h3,500, N1, N2);

Mh1=Mh1 (1:50,:);

P_t=[Mh1; Mt];

P_t=P_t';

Y_t=sim (net, P_t);

Pb=sum (round(Y_t (1,1:100)))/100

Оценка вероятности правильного обнаружения гусеничной техники Pb=1

Находим разницу желаемых и реальных выходов нейронной сети Е и определяем среднеквадратическую ошибку тестирования.

[Ek] = T-Y_t;

sqe_t = mse(Ek)

Величина среднеквадратической ошибки тестирования составляет:

sqe_t = 3.185e-025

Вывод: в данном разделе мы построили модель обнаружителя сейсмических сигналов на нейронной сети с обучением по методу обратного распространения ошибки. Задача обнаружения решается с не большими погрешностями, следовательно признаки подходят для обнаружения.

Данную двухслойную нейронную сеть можно применить в построении системы обнаружения объектов.

Заключение

Целью данной курсовой работы было изучение методов обработки информации и применение их для решения задач обнаружения объектов.

В ходе проделанной работы, которая выполнялась в четыре этапа, были получены следующие результаты:

1) Были построены гистограммы выборочных плотностей вероятности амплитуд сигналов, как случайных величин.

Оценены параметры распределения: математическое ожидание, дисперсию, среднеквадратическое отклонение.

Сделали предположение о законе распределения амплитуды и проверили гипотезу по критериям Колмогорова-Смирнова и Пирсона на уровне значимости 0,05. По критерию Колмогорова-Смирнова распределение подобрано, верно. По критерию Пирсона распределение подобрано верно только для фонового сигнала. Для него приняли гипотезу о нормальном распределении.

Приняли сигналы за реализации случайных функций и построили для них корреляционные функции. По корреляционным функциям определили, что сигналы имеют случайный колебательный характер.

2) Сформировали обучающее и контрольное множества данных (для обучения и контроля нейронной сети).

3) Для обучающей матрицы оценили параметры распределения признаков: математическое ожидание, дисперсию, среднее квадратическое отклонение. По каждому признаку обучающей матрицы заданных классов вычислили расстояние и выбрали признак с максимальной разностью. Вычислили порог принятия решения и построили на одном графике кривые плотности распределения вероятности. Сформулировали решающее правило.

4) Обучили двухслойную нейронную сеть на решение задачи классификации. Оценили вероятности правильного обнаружения и ложной тревоги. Те же показатели оценили по тестовым сигналам.

Список используемой литературы

1.   Лекции по теории обработки информации в СБЛ. Лектор: Чистова Г.К.

2.   Чистова Г.К. «Основы обработки и обнаружения случайных сигналов»

3.   Вентцель Е.С. «Теория вероятности и математическая статистика»