Обобщенная нормальная оценка
Численные методы решения
Вычислительные аспекты
Концепции построения математического обеспечения СПУРТ
Комплекс программ компоновщик расчетных схем
Основные функции КП Компоновщик расчетных схем
Отладка
Компоновка
Главное окно
Процедура обработки сообщений
Панель инструментов
Продолжить выполнение программы
Оконный редактор
Разработка мероприятий по безопасной эксплуатации ПЭВМ
Общие требования к организации и оборудованию рабочих мест с ВДТ и ПЭВМ
Навигация
Обобщенная нормальная оценка
Расчет и анализ потерь активной мощности
139305
знаков
0
таблиц
14
изображений
1.4 Обобщенная нормальная оценка
Этот метод соединяет в себе достоинства метода наименьших квадратов, байесовой оценки, метода регуляризации и дает возможность решать задачу в ее некорректной постановке, обеспечивая устойчивость вычислительного процесса и позволяя получать решение, наиболее близкое к истинному режиму ЭЭС. Сущность метода обобщенной нормальной оценки состоит в следующем.
К оценке состояния ЭЭС можно подойти с позиций решения системы нелинейных алгебраических уравнений
(1.14)
где: m – количество измеряемых параметров режима; n+1 – общее число узлов ЭЭС.
Если известны точные значения измеряемых параметров режима у, то решение x математической модели режима (1.14) существует; оно может быть единственным или неединственным (в последнем случае нужное решение локализуется после согласования области определения и области значений) [2].
Если известны приближенные значения правых частей (1.14)
(1.15)
где w – вектор случайных величин с математическим ожиданием М[w]=0, то для данной математической модели режима в пределах заданного уровня погрешности измерений существует целый класс режимов, для каждого из которых решение
(1.16)
может существовать (быть единственным или неединственным) или не существовать, а сколь угодно малые изменения измеряемых параметров могут приводить к сколь угодно большим изменениям решения [2]. По существу f отображает множество различных решений в пространстве оцениваемых параметров в неразличимое множество измерений в пространстве наблюдений.
Для некорректной модели режима требуется уточнить понятие «решение». Среди множества решений (1.15) естественно выбрать наиболее близкое к априорным данным 
и одновременно доставляющее измеряемым параметрам режима значения, близкие к измеренным 
. Если выбрать в качестве меры близости евклидову длину вектора, то этим требованиям отвечает решение, доставляющее минимум
, 
. (1.17)
Первое слагаемое (аналог обобщенного решения) характеризует близость измеренных и расчетных f(x) значений, второе слагаемое (аналог нормального решения) – близость априорных данных и решения x. Назначение параметра регуляризации 
– согласование меры близости в пространстве оцениваемых параметров и меры близости в пространстве наблюдений (косвенно решается проблема согласования области определения и области значений).
Решение, доставляющее минимум (1.17), называется обобщенным нормальным решением, а метод, реализующий этот критерий, – методом обобщенной нормальной оценки (МОНО).
Параметр регуляризации 
обобщенно учитывает статистические свойства измерений и априорных данных, его значение задается априори как
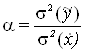
где: 
- дисперсия измерений; 
- дисперсия задания априорных данных.
При таком выборе параметра регуляризации МОНО дает неухудшающуюся, устойчивую к погрешности измерений и к изменениям параметра регуляризации оценку, а верхняя норма матрицы ковариации ошибок оценки оказывается минимальной.
В качестве априорной информации, используемой при оценке состояния реальной ЭЭС, можно использовать:
1) результаты предыдущей оценки;
2) измеренные значения напряжений (их номинальные значения); ограниченность фаз узловых напряжений (d ® 0).
Второй случай менее благоприятен. Часть априорных данных (например, измеренные напряжения) принадлежит области определения, другая часть (например, фазы узловых напряжений) может и не принадлежать к ним. Достоверность таких данных различна, полученная оценка параметра регуляризации находится в широком диапазоне (10¸105) [2]. Целесообразно для каждой группы априорных данных ввести свои весовые коэффициенты:
а) CU1 – для измеренных напряжений;
б) CU2 – для номинальных напряжений (если измерений не проводилось);
в) Сd – для фаз узловых напряжений.
Тогда критерий оценки перепишется в виде
,
где: 
– диагональная матрица с вышеуказанными весовыми коэффициентами, – априорные данные (для фаз узловых напряжений это значения на к-ой итерации).
Для реальных ЭЭС: CU1 =10-2, CU2 =10-4, Cd=1, и диапазон изменения параметра регуляризации сужается: 103<<105 [2]
Похожие работы
... (от передвижения источников загрязнения) 1180,48 Всего за год: 211845,25 10. Совершенствование системы электроснабжения подземных потребителей шахты Расчет схемы электроснабжения ЦПП до участка и выбор фазокомпенсирующих устройств Основными задачами эксплуатации современных систем электроснабжения горных предприятий являются правильное определение электриче ...
... luc – программа используется для разложения матрицы на треугольные сомножители; rluc – программа, которая отвечает за решение системы уравнений. 4. Разработка адаптивной системы управления режимами электропотребления 4.1 Функции автоматизированной системы Сбор, накопление и передача информации, характеризующей режим электропотребления комбината (информация о нагрузках). Сбор, накопление ...
... Еловка ТМН-2500/35 ±6×1,5% Ужурсовхоз ТМН-4000/35 ±6×1,5% 2. Характеристика задачи расчета, анализа и оптимизации режимов РЭС 110-35 кВ по напряжению, реактивной мощности и коэффициентам трансформации Питающие электрические сети напряжением 110 кВ, ...
... линиям относят линии, для которых верхняя граница интервала неопределенности потерь превышает установленную норму (например, 5%). 3. Программы расчета потерь электроэнергии в распределительных электрических сетях 3.1 Необходимость расчета технических потерь электроэнергии В настоящее время во многих энергосистемах России потери в сетях растут даже при уменьшении энергопотребления. При ...
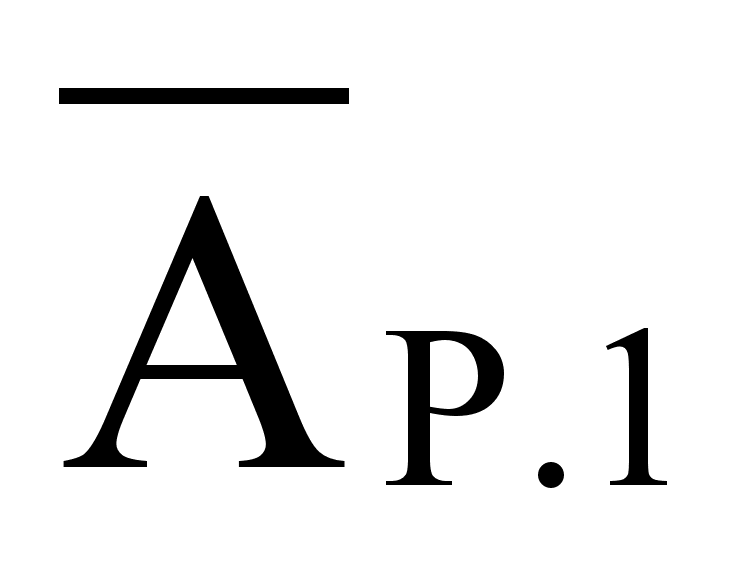
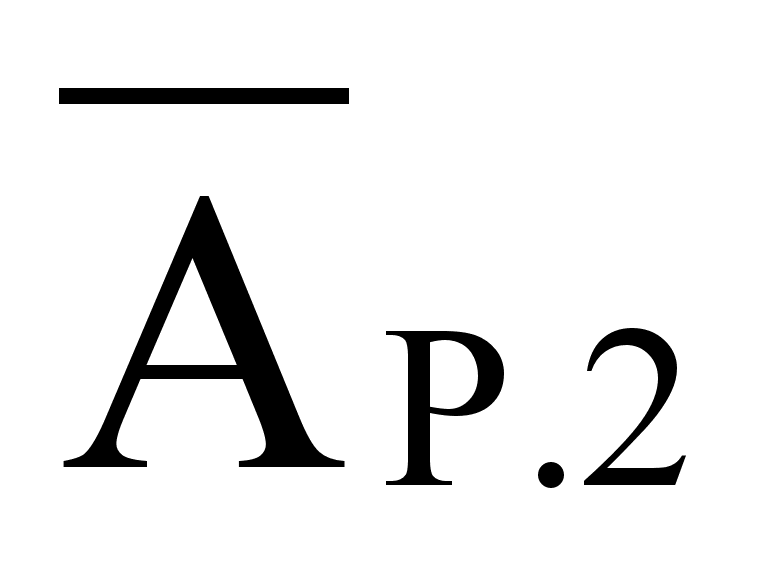
0 комментариев