Обобщенная нормальная оценка
Численные методы решения
Вычислительные аспекты
Концепции построения математического обеспечения СПУРТ
Комплекс программ компоновщик расчетных схем
Основные функции КП Компоновщик расчетных схем
Отладка
Компоновка
Главное окно
Процедура обработки сообщений
Панель инструментов
Продолжить выполнение программы
Оконный редактор
Разработка мероприятий по безопасной эксплуатации ПЭВМ
Общие требования к организации и оборудованию рабочих мест с ВДТ и ПЭВМ
Навигация
Численные методы решения
Расчет и анализ потерь активной мощности
139305
знаков
0
таблиц
14
изображений
1.5 Численные методы решения
Принимая во внимание все выше сказанное, в конечном счете задача оценивания состояния ЭЭС сводится к решению экстремальной задачи
(1.18)
по итерационной формуле
, (1.19)
где: k – номер итерации; 
– направление продвижения на (к+1) – ой итерации из точки хк; 
– коэффициент, определяющий длину шага в направлении ; 
– приращение на к-ой итерации; начальное приближение 
задается.
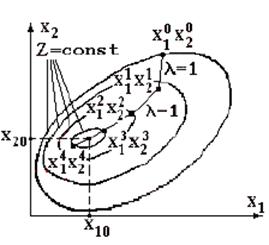
В результате решения (1.19) будет получена последовательность 
с определенными свойствами.
Для выбранной модели режима и построенного критерия оценки эффективность алгоритма оценки состояния ЭЭС определяется свойствами численного метода решения (1.19) и характеризуется такими критериями, как: скорость и надежность сходимости, точность решения, время счета, сложность алгоритма, требуемый объем оперативной памяти ЭВМ и т.д.
Численные методы решения (1.19) используют ту или иную аппроксимацию либо целевой функции
(1.20)
либо вектор-функции f(x). Наибольшее распространение получил метод Ньютона-Рафсона, в котором используется разложение в ряд Тейлора нелинейной вектор-функции f(x) в окрестности произвольной точки хк до членов первого порядка малости включительно
f (x) = f (xk) + fx(xk) (x – xk). (1.21)
Подстановка (1.21) в (1.20) дает:
Из необходимого условия минимума следует:
,
тогда приращение на к-ой итерации находится
,
где нижний индекс указывает, по какому вектор-аргументу осуществляется дифференцирование; x – xk = Dxk; x, xk – достаточно близкие точки.
Итерационный процесс (1.19) продолжается до достижения заданной точности расчетов e:
½D xk½ £ e.
Для уменьшения времени счета проверку можно производить только для модулей узловых напряжений.
Наличие стабилизирующей функции позволяет получить решение независимо от начального приближения, итерационный процесс сходится за две-четыре итерации, а число итераций в основном определяется качеством ТИ и «тяжестью» режима [2].
Оценка, вообще говоря, зависит от параметра регуляризации a. При завышенных значениях a возможно появление т.н. эффекта сглаживания, который может быть ослаблен, если воспользоваться следующим подходом.
Пусть на к-ом шаге методом Ньютона-Рафсона получена оценка хК и приращение DхК. Величина шага в направлении DхК может быть выбрана из условия достижения минимума суммы квадратов небалансов мощностей, т.е.
Приравняв 
к нулю и выразив из этого равенства 
, получим
.
Итерационный процесс, реализованный по формуле
, (1.22)
продолжается до тех пор, пока не будет нарушено условие
,
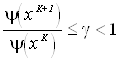где 
характеризует скорость уменьшения суммы квадратов небалансов мощностей (обычно принимается равной 0.99).
Метод Ньютона-Рафсона по параметру целесообразно использовать в двух случаях:
а) когда имеются точные значения измеряемых параметров режима у;
б) когда возникают затруднения с оценкой числового значения 
.
Учитывая вышеперечисленные достоинства метода обобщенной нормальной оценки, естественно будет использовать его в дальнейшем для оценки состояния ЭЭС.
Похожие работы
... (от передвижения источников загрязнения) 1180,48 Всего за год: 211845,25 10. Совершенствование системы электроснабжения подземных потребителей шахты Расчет схемы электроснабжения ЦПП до участка и выбор фазокомпенсирующих устройств Основными задачами эксплуатации современных систем электроснабжения горных предприятий являются правильное определение электриче ...
... luc – программа используется для разложения матрицы на треугольные сомножители; rluc – программа, которая отвечает за решение системы уравнений. 4. Разработка адаптивной системы управления режимами электропотребления 4.1 Функции автоматизированной системы Сбор, накопление и передача информации, характеризующей режим электропотребления комбината (информация о нагрузках). Сбор, накопление ...
... Еловка ТМН-2500/35 ±6×1,5% Ужурсовхоз ТМН-4000/35 ±6×1,5% 2. Характеристика задачи расчета, анализа и оптимизации режимов РЭС 110-35 кВ по напряжению, реактивной мощности и коэффициентам трансформации Питающие электрические сети напряжением 110 кВ, ...
... линиям относят линии, для которых верхняя граница интервала неопределенности потерь превышает установленную норму (например, 5%). 3. Программы расчета потерь электроэнергии в распределительных электрических сетях 3.1 Необходимость расчета технических потерь электроэнергии В настоящее время во многих энергосистемах России потери в сетях растут даже при уменьшении энергопотребления. При ...
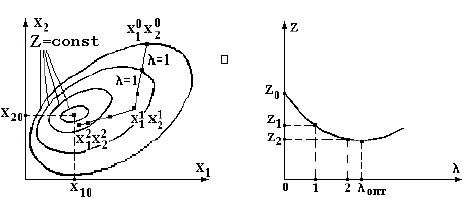
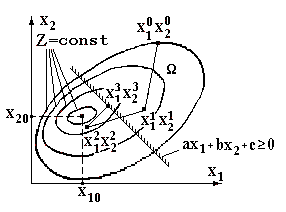
0 комментариев