Навигация
Модифицированный симплекс-метод
3. Модифицированный симплекс-метод
В основу данной разновидности симплекс-метода положены такие особенности линейной алгебры, которые позволяют в ходе решения задачи работать с частью матрицы ограничений. Иногда метод называют методом обратной матрицы.
В процессе работы алгоритма происходит спонтанное обращение матрицы ограничений по частям, соответствующим текущим базисным векторам. Указанная способность делает весьма привлекательной машинную реализацию вычислений вследствие экономии памяти под промежуточные переменные и значительного сокращения времени счёта. Способность хороша для ситуаций, когда число переменных n значительно превышает число ограничений m.
В целом, метод отражает традиционные черты общего подхода к решению задач линейного программирования, включающего в себя канонизацию условий задачи, расчёт симплекс – разностей, проверку условий оптимальности, принятие решений о коррекции базиса и исключение Жордана – Гаусса. Особенности заключаются в наличии двух таблиц – основной и вспомогательной, порядке их заполнения и некоторой специфичности расчётных формул.
Зная оптимальный план этой задачи, на основе соотношений получаем оптимальный план исходной задачи.
Таким образом, процесс нахождения решения задачи нелинейного программирования включает следующие этапы:
1. Первоначальную задачу сводят к задаче линейного программирования.
2. Находят решение линейной задачи
Используя соотношения, определяют оптимальный план исходной задачи и находят максимальное значение целевой функции нелинейной задачи.
Первый этап: Получение задания к курсовой работе
1. Все числовые данные, касающиеся предполагаемых производственных и экономических процессов, берутся на основе шестизначного шифра:
9 5 5 8 7 2
Под каждую цифру записываются буквы a, b, c, d, e, f в следующем виде:
9 5 5 8 7 2
а b c d e f
из последней строки таблицы индивидуальных заданий находим столбцы соответствующие буквам a, b, c, d, e, f. Тогда числовыми данными, необходимыми для выполнения данной курсовой работы, будут данные находящиеся в а – том столбце в строке 9, b – том столбце в строке 5, c – том столбце в строке 5, d – том столбце в строке 8, e – том столбце в строке 7и f – том столбце в строке 2.
По таблице исходных заданий для любого варианта заданий по столбцу а исполнитель получает вариант выполняемого задания. В моем случае для цифры 9 соответствует вариант 9.
На некотором заводе производится три вида продукта и при этом расходуется два вида ресурсов. Производственная функция каждого вида продукта на предприятии опишется равенствами:
![]()
где Сi и ![]() - постоянные величины, i = 1, 2, 3;
- постоянные величины, i = 1, 2, 3;
X1 – трудовые ресурсы в человеко-днях;
Х2 – денежно-материальные средства, в тенге;
Уi – получаемый продукт
Х1 = а1х1 + b1x2 + c1x3
Х2 = а2х1 + b2x2 + c2x3
Найти все неотрицательные базисные решения и определить оптимальный план F = y1 + y2 + y3.
Известно, что продукт для производства j – того вида затрачивается aij единиц i – того ресурса. Эти затраты даются в таблицах 3.9.1. – 3.9.10
Последующие числовые данные берутся только из таблицы исходных данных выбранного варианта задания т.е. из таблицы №3.9.11.
2. По столбцу таблицы №3.9.11 для строки 8 исходной таблицей затрат единиц ресурса, будет таблица №3.9.4 т.е. следующая таблица:
| Продукты ресурсы | 1 | 2 | 3 |
| I | 8 | 4 | 6 |
| II | 160 | 240 | 200 |
3. По столбцу c – на 3 строке находим с1=6, α1=0,6
4. По столбцу d – на 5 строке определяем с2=5, α2=0,5
5. По столбцу e – по 4 строке установим, что с3=8, α3=0,4.
6. И наконец по столбцу f – в 1 строке найдем Тчел.дней =1000, Птенге = 280000
Для производства имеются трудовые ресурсы Тчел.дней и денежно-материальные средства Птенге.
Требуется найти оптимальный план выпуска продукции, при котором выпускаемый продукт будет наибольшим.
Второй этап – составление математической модели задачи
1. На основании полученных в первом этапе исходных данных и описания заданного производственного процесса составляется следующая таблица:
| Продукты ресурсы | 1 | 2 | 3 |
|
| I | 8 | 4 | 6 | 1000 |
| II | 160 | 240 | 200 | 280000 |
Через Х1 обозначим ресурсы I вида.
Через Х2 обозначим ресурсы II вида.
2. Обращаясь к условиям задачи, определяем все возможные ограничения, объединяя их в систему ограничений.
8Х1 + 4Х2 + 6Х3 ≤ 1000
240Х1+ 200Х2 + 160Х3 ≤ 280000
Таким образом, получили задачу нелинейного программирования. Такие задачи называются задачами нелинейного программирования.
Решение задач нелинейного программирования осуществляется приведением их к задачам линейного программирования.
Для решения задачи линейного программирования применяется симплекс – метод.
Третий этап – выбор метода решения полученной математической задачи
Решение
1. Для решения задач линейного программирования симплекс – методом задача приводиться к каноническому виду:
8Х1 + 4Х2 + 6Х3 + Х4= 1000
240Х1+ 200Х2 + 160Х3 + Х5= 280000
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
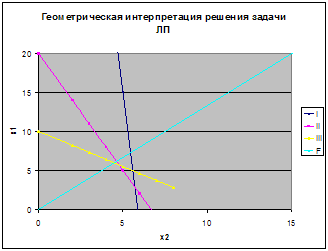
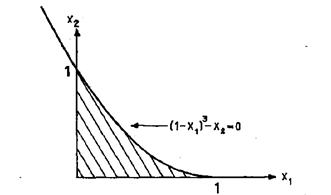
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
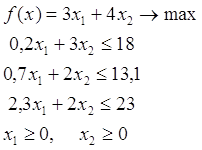
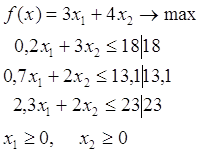
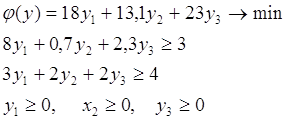
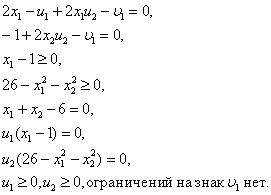





0 комментариев