Навигация
Находим получаемый продукт
2. Находим получаемый продукт.
Х1= 6*0+8*0+4*0=0
Х2=240*0+200*0+160*0=0
У1=3*00,4*00,6=0
У2=5*00,5*00,5=0
У3=8*00,6*00,4=0
F1=0+0+0=0
Х1= 6*0+8*325/2+4*0=1300
Х2=240*0+200*325/2+160*0=32500
У1=3*13000,4*325000,6=26904,728
У2=5*13000,5*325000,5=32500
У3=8*13000,6*325000,4=37688,542
F2=26904,728 +32500 +37688,542 = 97093,27
Х1= 6*650/3+8*0+4*0=1300
Х2=240*650/3+200*0+160*0=52000
У1=3*13000,4*520000,6=35699,794
У2=5*13000,5*520000,5=41109,610
У3=8*13000,6*520000,4=45483,862
F3= 35699,794+ 41109,610+ 45483,862= 122263,266
Х1= 6*0+8*0+4*325=1300
Х2=240*0+200*0+160*325=52000
У1=3*13000,4*520000,6=35699,794
У2=5*13000,5*520000,5=41109,610
У3=8*13000,6*520000,4=45483,862
F3= 35699,794+ 41109,610+ 45483,862= 122263,266
F1 < F2
F2 < F3
F3 = F4
Ответ: Fmax= 122263,266
Четвертый этап – подготовка словесного алгоритма решения задачи1. Вводим данные в таблицу
2. Выбираем разрешающий элемент:
2.1. Берем каждый неотрицательный элемент первой строки и делим на свободный член первой строки.
2.2. Находим среди всех деленных элементов минимальный.
2.3. Берем каждый неотрицательный элемент второй строки и делим на свободный член второй строки.
2.4. Находим среди всех деленных элементов минимальный.
2.5. Берем каждый неотрицательный элемент n-ой строки и делим на свободный член n-ой строки.
2.6. Находим среди всех деленных элементов минимальный.
2.7. Берем минимальные элементы первой, второй и n-ой строки и среди них находим минимальный (это и будет разрешающий элемент). При условии если минимальные элементы строк совпадают, берется элемент первой строки.
3. Вычисляем всю таблицу методом прямоугольника относительно разрешающего элемента:
3.1. Умножаем разрешающий элемент на элемент решаемой строки.
3.2. Отнимаем произведение соответствующего элемента решаемой строки на элемент разрешающего столбца решаемой строки
3.3. И делим ответ на разрешающий элемент.
3.4. Делим разрешающую строку на разрешающий элемент.
3.5. Берем каждый элемент разрешающей строки и делим на разрешающий элемент.
3.6. Всем элементам, кроме разрешающего элемента, разрешающего столбца присвоим (0)
3.7. Разрешающему элементу присвоим (1).
В индексе разрешающей строки присвоить индекс
4. Повторяем процедуру вычисления с 2 пункта.
5. В конечном результате находим все неотрицательные базисные решения. Подставляем значения и находим получаемый продукт.
6. Находим все F.
7. Выбираем наибольшую из них, которая будет являться оптимальным планом выпуска продукции.
Пятый этап – разработка программы для решения задачиPrivate Sub Form_Load()
Left = (Screen. Width – Width) \ 2
Top = (Screen. Height – Height) \ 2
End Sub
Private Sub Timer1_Timer()
Unload Form1
Load Form2
Form2. Show
End Sub
‘Объявление переменных
Public a As Integer
Public b As Integer
Public c As Integer
Public d As Integer
Public e As Integer
Public f As Integer
Public aa As Integer
Public ab As Integer
Public ac As Integer
Public ad As Integer
Public ae As Integer
Public af As Integer
Public ba As Integer
Public bb As Integer
Public bc As Integer
Public bd As Integer
Public be As Integer
be = Text17. Text
bf = Text18. Text
ca = Text19. Text
cb = Text20. Text
cc = Text21. Text
cd = Text22. Text
ce = Text23. Text
cf = Text24. Text
X1 = Text25. Text
X2 = Text26. Text
X3 = Text27. Text
‘Проверка выполнения равенств
If a*x1+aa*x2+ba*x3=ca Then «Равенство выполняется» Else «Равенство не выполняется»
If b*x1+ab*x2+bb*x3=cb Then «Равенство выполняется» Else «Равенство не выполняется»
If c*x1+ac*x2+bc*x3=cc Then «Равенство выполняется» Else «Равенство не выполняется»
If d*x1+ad*x2+bd*x3=cd Then «Равенство выполняется» Else «Равенство не выполняется»
If e*x1+ae*x2+be*x3=ce Then «Равенство выполняется» Else «Равенство не выполняется»
F= f*x1+af*x2+bf*x3
If F<fmin Then «Решение не выполняется» Else «Решение выполняется, план является оптимальным»
Text28. Visible = True
Text29. Visible = True
End Sub
Private Sub Command2_Click()
‘очистка текстовых окон для следующего ввода данных
Text1. Text = «»
Text2. Text = «»
Text3. Text = «»
Text4. Text = «»
Text5. Text = «»
Text6. Text = «»
Text7. Text = «»
Text8. Text = «»
Text9. Text = «»
Text10. Text = «»
Text11. Text = «»
Text12. Text = «»
Text13. Text = «»
Text14. Text = «»
Text15. Text = «»
Text16. Text = «»
Text17. Text = «»
Text18. Text = «»
Text19. Text = «»
Text20. Text = «»
Text21. Text = «»Text22. Text = «»
Text23. Text = «»
Text24. Text = «»
Text25. Text = «»
Text26. Text = «»
Text27. Text = «»
Text28. Visible = False
Text29. Visible = False
End Sub
Private Sub Command3_Click()
‘показать справку
Unload Form2
Load Form3
Form3. Show
End Sub
Private Sub Command4_Click()
Unload Form2
End Sub
Private Sub Form_Load()
Left = (Screen. Width – Width) \ 2
Top = (Screen. Height – Height) \ 2
‘подготовка текстовых окон к вводу данных при запуске рабочего окна
Text1. Text = «»
Text2. Text = «»
Text3. Text = «»
Text4. Text = «»
Text5. Text = «»
Text6. Text = «»
Text7. Text = «»
Text8. Text = «»
Text9. Text = «»
Text10. Text = «»
Text11. Text = «»
Text12. Text = «»
Text13. Text = «»
Text14. Text = «»
Text15. Text = «»
Text16. Text = «»
Text17. Text = «»
Text18. Text = «»
Text19. Text = «»
Text20. Text = «»
Text21. Text = «»
Text22. Text = «»
Text23. Text = «»
Text24. Text = «»
Text25. Text = «»
Text26. Text = «»
Text27. Text = «»
End Sub
Private Sub Form_Load()
Left = (Screen. Width – Width) \ 2
Top = (Screen. Height – Height) \ 2
End Sub
Private Sub Timer1_Timer()
Unload Form3
Load Form2
Form2. Show
End Sub
Результат использования программы
Ввод начальных коэффициентов
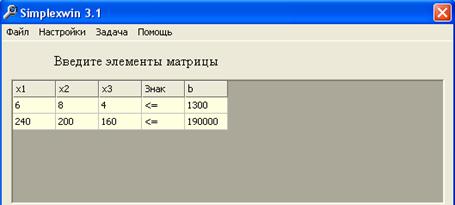
Полученное решение
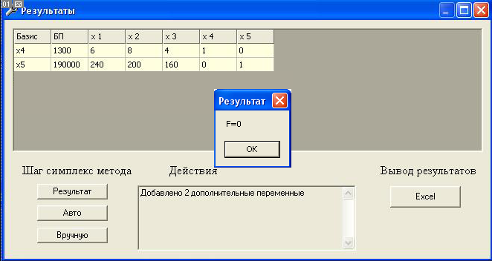
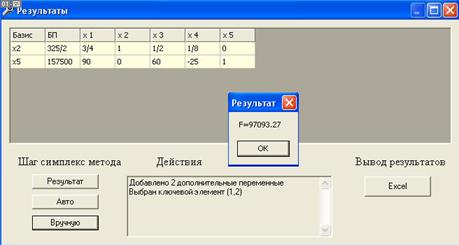
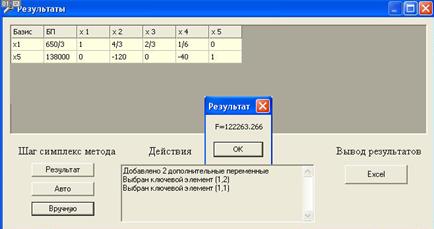
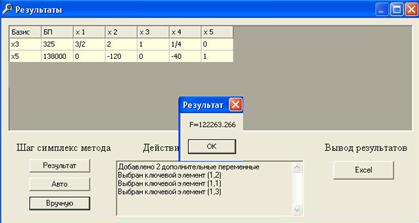
Конечный результат
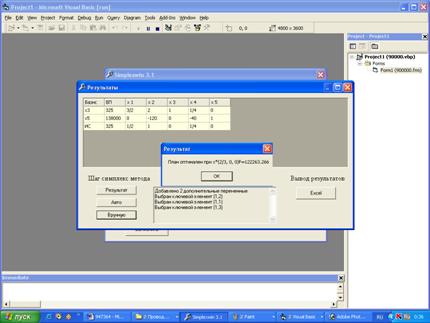
Список используемой литературы
1. Методические рекомендации «Курсовая работа по моделированию производственных и экономических процессов» Талдыкорган. 1999 г.
2. Уолш Б. «Программирование на Бейсике» Пер. с анг. – Москва: Радио и связь, 1998 г.
3. Фиакко А., Маккормик Г. «Нелинейное программирование» Пер. С анг. – Москва: Мир, 1988 г.
4. Солодовников А.С. «Введение в линейную алгебру и линейное программирование» Москва, «Просвещение», 1996 г.
5. Кузнецов Ю.Н. и др. «Математическое программирование» Москва, «Высшая школа», 1980 г.
 | |||
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
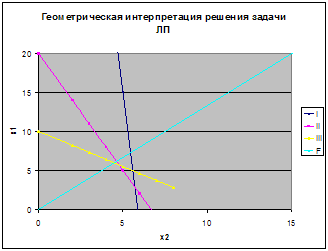
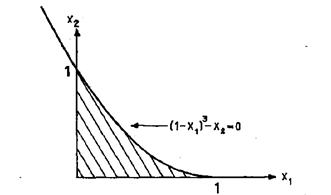
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
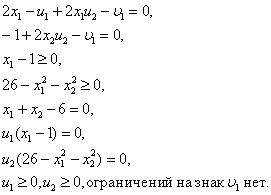





0 комментариев