Навигация
Составляем таблицу и определяем все неотрицательные базисные решения системы
2. Составляем таблицу и определяем все неотрицательные базисные решения системы.
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Свободный член |
| Х4 | 8 | 4 | 6 | 1 | 0 | 1000 |
| Х5 | 240 | 200 | 160 | 0 | 1 | 280000 |
А) Нашли некоторое неотрицательное базисное решение: Х4 =1300, Х5 = 190000. По заданию продолжаем искать базисные решения. Разрешающим элементом выбираем в 1 строке – Х2. Соответственно вся строка делится на 8, а все остальные элементы находятся по правилу прямоугольника.
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Свободный член |
| Х4 | 8 | 4 | 6 | 1 | 0 | 1000 |
| Х5 | 240 | 200 | 160 | 0 | 1 | 280000 |
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Свободный член |
| Х2 | ¾ | 1 | ½ | 1/8 | 0 | 325/2 |
| Х5 | 90 | 0 | 60 | -25 | 1 | 157500 |
Б) Нашли некоторое неотрицательное базисное решение: Х2 =325/2, Х5 =157500. По заданию продолжаем искать базисные решения. Разрешающим элементом выбираем в 1 строке – Х1. Соответственно вся строка делится на 3/4, а все остальные элементы находятся по правилу прямоугольника.
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Свободный член |
| Х2 | ¾ | 1 | ½ | 1/8 | 0 | 325/2 |
| Х5 | 90 | 0 | 60 | -25 | 1 | 157500 |
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Свободный член |
| Х1 | 1 | 4/3 | 2/3 | 1/6 | 0 | 650/3 |
| Х5 | 0 | -120 | 0 | -40 | 1 | 138000 |
В) Нашли некоторое неотрицательное базисное решение: Х1 =650/3, Х5 =138000. По заданию продолжаем искать базисные решения. Разрешающим элементом выбираем в 1 строке – Х3. Соответственно вся строка делится на 2/3, а все остальные элементы находятся по правилу прямоугольника.
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Свободный член |
| Х1 | 1 | 4/3 | 2/3 | 1/6 | 0 | 650/3 |
| Х5 | 0 | -120 | 0 | -40 | 1 | 138000 |
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Свободный член |
| Х3 | 3/2 | 2 | 1 | 1/4 | 0 | 325 |
| Х5 | 0 | -120 | 0 | -40 | 1 | 138000 |
Г) Нашли некоторое неотрицательное базисное решение: Х5 =138000, Х3 =325. Найдены все неотрицательные базисные решения.
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
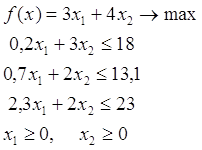
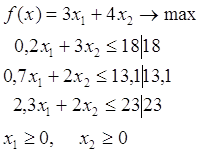
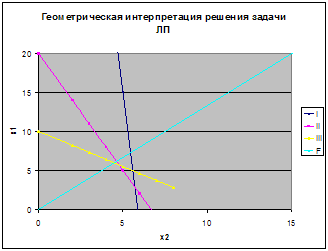
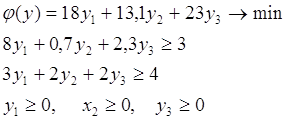





0 комментариев