Навигация
Криптограма Y передається по лінії зв'язку адресату
4. Криптограма Y передається по лінії зв'язку адресату.
5. Адресат розшифровує криптограму Y, використовуючи той же
ключ k і відображення Ек-1, зворотне до відображення Ек, і читає повідомлення X:
Х = Ек-1(Y).
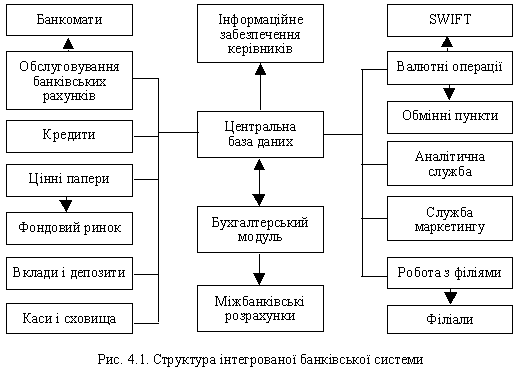
Пояснимо важливі особливості даного протоколу за допомогою схеми, приведеної на рис. 1.4.
Крок 2 протоколу реалізується або за допомогою посередника, третьої сторони, яку можна умовно назвати центром генерації і розподілу ключів (ЦГРК), або функції ЦГРК покладаються на абонентів. У першому випадку криптографічний протокол зв'язку шифру називають трибічним, а в другому випадку – двостороннім.

![]()
![]() Захищений
Захищений
канал зв’язку
Х k k Х
![]()
![]()
|
|
![]()
|
![]() k
k
Рис. 1.4
Істотною особливістю протоколу є секретність ключа k, який передається відправнику і адресату або у відкритому вигляді по каналу зв'язку, захищеному від дій криптоаналітика, або в шифрованому вигляді по лінії зв'язку.
Захищеній канал зв’язку може мати відносно невисоку пропускну спроможність, але повинен надійно захищати ключову інформацію від несанкціонованого доступу. Ключ повинен залишатися у секреті до, під час і після реалізації протоколу, інакше зловмисник, заволодівши ключем, може розшифрувати криптограму і прочитати повідомлення. Відправник і адресат можуть виконати крок 1 протоколу публічно (секретність шифрсистеми необов'язкова), але крок 2 вони повинні виконати таємно (секретність ключа обов'язкова).
Така необхідність викликана тим, що лінії зв'язку, в особливості протяжні, уразливі з погляду втручання пасивного і активного супротивників.
Пасивний супротивник (криптоаналітик), бажаючи дістати доступ до повідомлення X, контролює лінію зв'язку на кроці 4 протоколу. Не втручаючись в реалізацію протоколу, він перехоплює криптограму Y з метою розкриття шифру.
Розробляючи криптосистему, криптограф звичайно виходить з наступних припущень про можливості криптоаналітика:
1) криптоаналітик контролює лінію зв'язку;
2) криптоаналітику відомий пристрій сімейства Е відображень шифру;
3) криптоаналітику невідомий ключ k, тобто невідомо відображення Ек, яке використане для отримання криптограми Y.
У цих умовах криптоаналітик намагається вирішити наступні завдання, які називаються завданнями дешифрування:
1. Визначити відкритий текст X і використаний ключ k по перехопленій криптограмі Y, тобто побудувати алгоритм дешифрування y такий, що
y( Y) = (Х, k).
2. Визначити використаний ключ по відомим відкритому і шифрованому текстам, тобто побудувати алгоритм дешифрування такий, що
j(Х, Y) = к.
Така постановка задачі має сенс, коли криптоаналітик перехопив декілька криптограм, одержаних з використанням ключа k, і має в своєму розпорядженні відкриті тексти не для всіх перехоплених криптограм. В цьому випадку, вирішивши завдання дешифрування другого типу, він прочитає всі відкриті тексти, зашифровані з використанням ключа k.
3. Визначити використовуваний ключ k по спеціально підібраному відкритому тексту X і по відповідному шифрованому тексту Y, тобто побудувати алгоритм дешифрування jХ такий, що
jХ(Y) = к.
Подібна постановка задачі вникає тоді, коли криптоаналітик має можливість тестування криптосистеми, тобто генерування криптограми для спеціально підібраного відкритого тексту. Частіше така можливість виникає при аналізі асиметричних систем.
Дешифрувальні задачі першого типу відрізняються вищою обчислювальною складністю в порівнянні із задачами другого і третього типу. Найменшу обчислювальну складність мають задачі тестування.
Активний супротивник порушує реалізацію протоколу. Він може перервати зв'язок на кроці 4, вважаючи, що відправник не зможе більше ніщо повідомити адресату. Він може також перехопити повідомлення і замінити його своїм власним. Якби активний узнав ключ (контролюючи крок 2 або проникнувши в криптосистему), він міг би зашифрувати своє повідомлення і відправити його адресату замість перехопленого повідомлення, що не викликало б у останнього ніяких підозр. Якщо активний супротивник не знає ключа, то він може створити лише таке шифроване повідомлення, яке при розшифруванні перетворюється на випадкову послідовність символів.
Розглянутий протокол має на увазі взаємну довіру відправника, адресата і третьої сторони в особі ЦГРК. Це є слабкістю даного протоколу, оскільки не завжди можна виключити взаємний обман дійових осіб протоколу. Втім, абсолютних гарантій бездоганності того або іншого протоколу не існує, оскільки виконання будь-якого протоколу зв'язане за участю людей і залежить, зокрема, від надійності дійових осіб протоколу.
Таким чином, по організації секретного зв'язку з використанням симетричної криптосистеми можна зробити наступні висновки:
1. Протокол повинен захищати відкритий текст і ключ від несанкціонованого доступу сторонньої особи на всіх етапах передачі інформації від джерела до одержувача повідомлень. Секретність ключа важливіша, чим секретність декількох повідомлень, що шифруються на цьому ключі. Якщо ключ скомпрометований (вкрадений, вгаданий, розкритий, викуплений), тоді супротивник, що має ключ, може розшифрувати всі повідомлення, зашифровані на цьому ключі. Крім того, супротивник зможе імітувати одну із сторін, що переговорюються, і генерувати фальшиві повідомлення ввести в оману іншу сторону. Якщо часто змінювати ключі, ця проблема зводиться до мінімуму.
2. Протокол не повинен допускати виходу в лінію зв'язку «зайвої» інформації, що надає криптоаналітику супротивника додаткові можливості дешифрування криптограм. Протокол повинен захищати інформацію не тільки від сторонніх осіб, але і від взаємного обману дійових осіб протоколу.
3. Якщо допустити, що кожна пара користувачів мережі зв'язку
застосовує окремий ключ, то число необхідних ключів дорівнює
п(п-1)/2 для п користувачів. Це означає, що при великому п генерація, зберігання і розподіл ключів стає трудомісткою проблемою.
Розглянемо тепер організацію секретного зв'язку з використанням асиметричної криптосистеми. Послідовність дій виглядає таким чином:
1. Відправник і адресат домовляються про використовувану асиметричну криптосистему.
2. Адресат посилає відправнику відкритий ключ k.
3. Відправник шифрує відкритий текст X за допомогою відкритого
ключа k, тобто створює криптограму Y = Еk(X).
4. Криптограма Y передається по лінії зв'язку адресату.
5. Адресат розшифровує криптограму Y, використовуючи закритий ключ z, і читає повідомлення X:
X = Еz(X).
Поза сумнівом, даний протокол захищає повідомлення X: пасивний супротивник може перехопити відкритий ключ і криптограму Y, але не може розшифрувати повідомлення, оскільки немає закритого ключа.
Гідністю протоколу є те, що він не вимагає розподілу секретних ключів. У мережі зв'язку нерідко відкриті ключі всіх користувачів поміщаються в загальнодоступну базу даних, а закриті ключі зберігаються у користувачів. Це спрощує протокол, оскільки відправник сам виконує крок 2 протоколи, не чекаючи дії адресата. Адресат не бере участь в протоколі до тих пір, поки не збереться прочитати відкрите повідомлення.
Висновки
Можна відмітити динамічний характер оцінок криптографічної стійкості шифрів. Ці оцінки необхідно час від часу переглядати у зв’язку із розвитком обчислювальних засобів і прогресом у області розробки методів дешифрування.
На практиці алгоритми з відкритим ключем не замінюють симетричних алгоритмів. Як правило, вони використовуються для шифрування не самих повідомлень, а ключів або деяких інших «допоміжних» інформаційних блоків відносно невеликої довжини. Це викликано наступними обставинами:
1. Продуктивність алгоритмів з відкритим ключем (швидкість шифрування) принаймні в 1000 разів поступається продуктивності симетричних алгоритмів, що ставить їх в невигідне становище при шифруванні великих об'ємів інформації.
2. Криптосистеми з відкритим ключем уразливі до атак на основі
підібраного відкритого тексту, особливо коли число варіантів блоку
відкритого тексту обмежене і допустимо перебір цих варіантів.
Тому найбільш вигідним представляється протокол секретного зв'язку з використанням гібридної криптосистеми, в якому асиметричний алгоритм використовується для засекречування і розподілу ключів зв’язку, а алгоритм із секретним ключем використовується для захисту даних. Крім того, такий протокол допускає знищення секретного сеансового ключа одразу після закінчення сеансу, що різко зменшує небезпеку його компрометації.
Розділ 2. Моделі елементів захищених систем 2.1. Поняття стійкості шифрсистеми
Абстрактно кажучи, стійкість криптографічної системи є мірою стійкості системи до атак. Система називається стійкою, якщо зловмисник не може зламувати її дуже часто або дуже швидко. Отже, для вимірювання стійкості системи необхідно оцінювати імовірність злому і об'єм обчислювальних витрат.
Щоб конкретизувати наші міркування, розглянемо «ігрову атаку», яка розігрується між Зловмисником і законним Учасником сеансу зв’язку. Ця гра дозволить продемонструвати обчислювальні аспекти, пов'язані з поняттям стійкості.
Для опису криптосистеми вважатимемо, що вона складається з алгоритму шифрування Y, простору початкових текстів М і простору зашифрованих текстів С. Однак, слід зробити одне важливе зауваження: алгоритм шифрування Y вважається імовірнісним, тобто містить внутрішню випадкову операцію, що має якийсь розподіл імовірності. Таким чином, зашифрований текст представляє собою випадкову величину, що має той же самий розподіл. Наприклад, якщо вихідне повідомлення двічі шифрується за допомогою одного і того ж ключа шифрування, з великою імовірності виникнуть два різних зашифрованих текста (оскільки алгоритм шифрування є однозначним перетворенням).
Ігрова атака описується наступним протоколом .
Попередні умови:
а) Зловмисник і законний Учасник діють в заданій криптосистемі, що складається з алгоритму шифрування Y, простору початкових повідомлень М і простору зашифрованих текстів С;
б) законний Учасник володіє фіксованим ключем шифрування k.
1. Зловмисник підбирає різні повідомлення m0, m1 Î М і посилає їх учаснику. Повідомлення m0, m1 називаються підібраним початковим текстом (chosen plaintext messages). Зловмисник поки знаходиться на етапі пошуку ("find-stage") повідомлень m0, m1. Зрозуміло, він готує їх так, щоб легко розпізнати результат їх шифрування.
2. Якщо ці повідомлення мають різну довжину, Учасник доповнює коротше з них, щоб їх довжини стали однаковими. Наприклад, для доповнення повідомлень він може використовувати фіктивний рядок 0d, де d – різниця між довжинами повідомлень. Учасник підкидає ідеальну монету bÎ{0,1} і виконує наступну операцію шифрування
с* = 
Учасник посилає Зловмиснику повідомлення с* Î С. Зашифроване повідомлення с* називається зашифрованим текстом оклику (challenge ciphertext). Слід пам'ятати, що зашифрований текст с* є випадковою величиною, залежною від двох випадкових вхідних величин: ідеальної монети b і внутрішньої випадкової операції алгоритму Y.
3. Одержавши зашифрований текст с*, Зловмисник повинен вгадати результат підкидання монети, надіславши учаснику 0 або 1. Тепер Зловмисник знаходиться на етапі осмисленого вгадування ("guess-stage" for an educated guess), намагаючись вгадати результат жеребкування, проведеного учасником. Відповіді, що відрізняються від 0 і 1, не допускаються.
У цій грі учасник пропонує зловмиснику відповісти на наступне питання. Результатом якого з експериментів Yk(m0) чи Yk(m1) є оклик с*?
Вважатимемо, що Зловмисник застосовує імовірнісний поліноміальний алгоритм розпізнавання. Позначимо через Adv перевагу Зловмисника, з яким він може розпізнавати відмінність між зашифрованими текстами. Вона дорівнює різниці між ймовірностями, з якими Зловмисник може розпізнати експерименти Yk(m0) чи Yk(m1).
Adv = | Prob[0 ¬ Зловмисник(с* = Yk(m0))] – Prob[0 ¬ Зловмисник(с* = =Yk(m1))]|. (2.1)
Імовірнісний простір повинен містити випадковий вибір, зроблений Учасником і Зловмисником, а також внутрішню випадкову операцію алгоритму шифрування. Відзначимо, що відповідь Зловмисника залежить не тільки від зашифрованого тексту оклику с*, але і від двох підібраних початкових повідомлень (m0, m1). Тільки тому його відповідь можна вважати результатом «осмисленого вгадування» («educated guess»).
Слід відмітити, що Зловмисник має додаткову можливість для того, щоб поліпшити результати свого вгадування: Учасник підкидає ідеальну монету. Формула обчислення переваги (2.1.1) не указує явно на те, як Зловмисник може скористатися цим фактом, хоча неявно відомо, що кожна з імовірності, що входить у формулу (2.1.1), ніколи не перевищить ![]() , наприклад, імовірность події с* = Yk(m0) складає рівно
, наприклад, імовірность події с* = Yk(m0) складає рівно ![]() . Необхідно явно вказати, як саме Зловмисник використовує додатковий ключ у формулі обчислення переваги. Застосовуючи умовну імовірность і помічаючи, що імовірность обох результатів при підкиданні ідеальної монети рівна
. Необхідно явно вказати, як саме Зловмисник використовує додатковий ключ у формулі обчислення переваги. Застосовуючи умовну імовірность і помічаючи, що імовірность обох результатів при підкиданні ідеальної монети рівна ![]() , можна переписати формулу (2.1.1) в наступному вигляді
, можна переписати формулу (2.1.1) в наступному вигляді
Adv = |![]() Prob[0 ¬ Зловмисник(с* = Yk(m0))] –
Prob[0 ¬ Зловмисник(с* = Yk(m0))] –
- ![]() Prob[0 ¬ Зловмисник(с*=Yk(m1))]|. (2.2)
Prob[0 ¬ Зловмисник(с*=Yk(m1))]|. (2.2)
Згідно з правилами гри Зловмиснику не дозволяється давати відповіді, які відрізняються від 0 та 1, тому неправильна відповідь є подією, додатковою по відношенню до правильної відповіді. З цього випливає наступна формула
Adv = |![]() Prob[0 ¬ Зловмисник(с* = Yk(m0))] –
Prob[0 ¬ Зловмисник(с* = Yk(m0))] –
- ![]() (1 – Prob[0 ¬ Зловмисник(с*=Yk(m0))] )|.
(1 – Prob[0 ¬ Зловмисник(с*=Yk(m0))] )|.
Тобто
Prob[0 ¬ Зловмисник(с* = Yk(m0))] = ![]() ± Adv. (2.3)
± Adv. (2.3)
Формула (2.3) часто застосовується для виразу переваги алгоритму при вгадуванні результатів підкидання ідеальної монети. Отже, якщо Adv = 0, то випадкова відповідь Зловмисника має такий самий розподіл, як і результати підкидання ідеальної монети. Проте слід враховувати, що перевага завжди більше нуля. Очевидно, що формула (2.1.3) також справедлива, якщо в результатах жеребкування всі нулі замінити одиницями.
З формули (2.3) виходить, що перевага Зловмисника ніколи не перевищує ![]() , оскільки імовірність завжди лежить в інтервалі [0,1]. Дійсно, якщо Учасник шифрує обидва початкові тексти з імовірністю
, оскільки імовірність завжди лежить в інтервалі [0,1]. Дійсно, якщо Учасник шифрує обидва початкові тексти з імовірністю ![]() , перевагу Adv, що задана формулою (2.1), є різниця імовірності сумісних подій і ніколи не перевищує
, перевагу Adv, що задана формулою (2.1), є різниця імовірності сумісних подій і ніколи не перевищує ![]() . Можна відмітити, що формула (2.1.3) виглядає так, ніби Учасник підкидає несиметричну монету, наприклад, Учасник з імовірністю
. Можна відмітити, що формула (2.1.3) виглядає так, ніби Учасник підкидає несиметричну монету, наприклад, Учасник з імовірністю ![]() шифрує повідомлення m0 і з імовірністю
шифрує повідомлення m0 і з імовірністю ![]() - повідомлення m1.
- повідомлення m1.
Досліджувана криптосистема стійка по відношенню до ігрової атаки, якщо експеримент Yk(m0) не можливо відрізнити від експерименту Yk(m1). Це означає, що при будь-якій значущій перевазі Adv не повинно існувати жодного поліноміального алгоритму розпізнавання. Інакше кажучи, перевага, з якою Зловмисник може розрізняти результати шифрування, повинна бути дуже малою величиною в порівнянні з параметром безпеки схеми шифрування, яким, як правило, є довжина ключа шифрування. Можна вважати, що перевага будь-якого поліноміального алгоритму розпізнавання, що вживається Зловмисником, задається функцією, що повільно росте, залежною від об'єму обчислювальних ресурсів. Тут термін «повільно росте» означає, що, навіть якщо Зловмисник різко збільшить об'єм своїх обчислювальних ресурсів, перевага збільшиться украй трохи.
Стійкість розглянутої системи називається семантичною стійкістю. Тобто зашифрований текст не допускає ніякого витоку корисної інформації про вихідний текст( якщо не вважати корисною інформацією довжину самого вихідного тексту) жодному зловмиснику, який має поліноміально обмежені обчислювальні ресурси.
2.2. Стійкість криптографічних протоколівЯк і у випадку криптографічних алгоритмів, головне питання полягає в тому, наскільки стійким є той чи інший криптопротокол. Відповідь на нього можна знайти при зрівнянні цілого ряду факторів. Однак, оскільки в основі багатьох криптопротоколів лежать криптографічні алгоритми, зрозуміло, що остаточна стійкість буде не більше стійкості використовуваних криптографічних алгоритмів. Вона може бути понижена в наступних випадках:
- використання слабких криптографічних алгоритмів і некоректна реалізація деяких його складових;
- некоректна логіка роботи криптопротокола;
- некоректне використання криптографічних алгоритмів.
Труднощі першої категорії вирішуються в межах класичної криптографії. Типовим прикладом у цьому сенсі є використання слабких генераторів випадкових чисел.
Проблеми, що відносяться до другої категорії, найбільш поширені. На практиці саме по цих «больових крапках» звичайно проводяться атаки на криптопротоколи. Активний порушник може робити вплив на функціонування криптопротоколу шляхом наступних атак:
- атака з відомим ключем. Зловмисник, одержавши ключ попередньої сесії, намагається дізнатися ключ нової сесії;
- повторна передача. Перехопивши в попередніх сесіях певну порцію інформації, зловмисник передає її в подальших сесіях;
- підміна сторони інформаційного обміну. В процесі встановлення сеансу зв'язку між легальними користувачами зловмисник у разі подібної атаки намагається видати себе за одного з них або ініціювати від імені легального користувача встановлення зв'язку;
- атака із словником. Полягає в підборі пароля, що містить слова, що найбільш часто зустрічаються, або комбінацію буква/цифра. Звичайно перетворені за допомогою неключової хэш-функції паролі зберігаються у файлах на комп'ютері. Завдання зловмисника полягає в тому, щоб одержати шуканий файл, перетворити свій словник за допомогою даної хэш-функції і провести порівняння з метою знайти співпадаючі значення;
- підміна повідомлень. Проводиться шляхом заміни під час роботи криптопротокола повідомлень або даних.
Як приклад успішної атаки такого типу розглянемо криптопротокол розподілу секретних сеансових ключів між двома учасниками інформаційного обміну. Авторами цього методу є Нідхем і Шредер. Уразливість цього криптопротоколуа вперше була виявлена Денінгом і Сакко. Кожен учасник даного протоколу повинен розділити знання свого секретного ключа з сервером аутентифікації. Протокол складається з наступних кроків:
1. А → S: А, В, Na. Учасник А посилає запит серверу S, в якому він указує, що необхідно встановити сеанс зв'язку з учасником В. У даному запиті присутні наступні значення:
- А і В – імена або ідентифікатори учасників;
- N – унікальне для даного сеансу число; використовується для запобігання повторним передачам шляхом включення його в подальші повідомлення.
2. S → A: { Na, В, Кab, { Кab, А}Kbs}Kas.Сервер відповідає повідомленням, зашифрованим на секретному ключі сервер-учасник А (Кas), в якому знаходиться сеансовий ключ (Кab), а також ще одна копія цього ключа, зашифрованого на секретному ключі сервер-учасник В (Кbs).
3. А → B: { Кab, А}Кbs Учасник В розшифровує дане повідомлення, оскільки йому відомий ключ Кbs; в результаті він одержує ключ Кab.
4. B → A: {Nb}Kab. Дане повідомлення учасник В посилає для того, щоб переконатися, що А володіє ключем Кab, і показати учаснику А своє знання Кab.
5. А → B: {Nb – 1} Кab. Учасник А доводить своє володіння ключем Кab, і на цьому протокол закінчує свою роботу, в результаті учасники А і В одержують загальний секретний сеансовий ключ Кab.
Уразливість даного криптопротокола полягає в тому, що якщо сеансовий ключ К1ab із попередньої сесії був скомпрометований, то зловмисник (позначимо його через З), що дістав можливість контролю мережевого трафіку на кроці 3 нової (нескомпрометованої) сесії, перехоплює повідомлення (А → В: { Кab, A}Kbs) і замість нього посилає повідомлення (З → В: { К1ab, A}Кbs). Учасник B відповідає повідомленням (B → A: {Nb}К1ab), вважаючи, що А бажає встановити з ним нову сесію з ключем К1ab. З, одержуючи дане повідомлення, розшифровує його і відправляє В повідомлення (З → В: {Nb – 1}К1ab). Таким чином, З встановлює сесію з В від імені А.
З погляду розуміння можливих наслідків, що виникають при виявленні недоробок в логіці роботи криптопротокола, цей приклад є дуже показовим. Для усунення подібних проблем були спеціально розроблені засоби і методи аналізу коректності побудови логіки роботи криптопротоколів. Застосування формальних методів дозволяє також виявити комунікаційну надмірність в крип-топротоколах, що є важливим плюсом в умовах постійно зростаючих вимог до оперативності обробки інформації в сучасних мережах передачі даних.
Третя група атак, що істотно знижують рівень безпеки при використанні криптопротоколів, є найменш поширеною. Про це, принаймні, можна судити по частоті їх використання зловмисниками. Але з іншого боку, через їх важке виявлення, такі спроби є найбільш небезпечними, оскільки вони багато в чому залежать від математичних властивостей використовуваних криптографічних алгоритмів. Подібні вразливі місця не піддаються формальному аналізу і тому не можуть виявлятися навіть при використанні добре вивчених криптопротоколів. Особливо характерний поява «слабких крапок» при використанні асиметричних алгоритмів, оскільки вони в основному побудовані на неможливості ефективного рішення деяких математичних задач і не піддаються строгим математичним доказам і дослідженням за допомогою формальних методів.
Для прикладу проведемо доказ стійкості криптопротокола «уявний покер». Для початку необхідно розглянути сам протокол.
Для того, щоб зіграти в покер, гравці А і Б спочатку повинні чесно роздати карти. Слово «чесно» означає, що при роздачі карт А і Б повинні дотримуватися чотирьох правил.
1. Всі карти повинні роздаватися з однаковою імовірністю (тобто рівномірно), причому одна і та ж карта не повинна опинитися у двох різних гравців одночасно.
2. А і Б повинні знати карти, якими вони володіють, а інші гравці не повинні знати, які карти знаходяться на руках їх партнерів.
3. А і Б повинні підозрюватися в шахрайстві і порушенні правил протоколу.
4. А і Б повинні мати можливість перевіряти, чи чесно була зіграна попередня гра.
Ідея, що лежить в основі уявного покеру, полягає в застосуванні шифру, що володіє властивістю комутативності. Застосовуючи такий шифр, А і Б можуть двічі шифрувати повідомлення, використовуючи свої секретні ключі, і повинні двічі розшифровувати його. Хай
С = ЕХ( М) і М = DX(C)
означають алгоритми шифрування і розшифрування, що виконуються користувачем X. Комутативна властивість шифру полягає в тому, що для будь-якого повідомлення М виконуються наступні рівняння.
М = DA(DB(EA(EB(M)))) = DB(DA(EB(EA(M)))). (2.4)
Іншими словами, вихідне повідомлення можна відновити шляхом подвійного розшифрування незалежно від порядку шифрування.
Для простоти припустимо, що А і Б вирішили роздати по одній карті, використовуючи колоду, що складається з трьох карт. Спосіб чесної роздачі карт описується наступним протоколом.
Протокол чесної роздачі карт при грі в уявний покер.
Попередні умови:
А і Б погодили комутативний шифр, що володіє властивістю (2.4), і згенерували свої секретні ключі шифрування. Колода складається з трьох карт: М1, М2 і М3.
Мета:
Чесна роздача по одній карті кожному гравцю за правилами 1 – 4 .
1. А шифрує три карти таким чином: Сі = ЕА( М), де і = 1,2,3. Він посилає Б ці три зашифровані тексти у випадковому порядку. (Передача зашифрованих текстів у випадковому порядку еквівалентна перетасовуванню колоди.)
2. Б випадковим чином витягує один із зашифрованих текстів. Позначимо його через С. Потім він двічі шифрує його як СС = ЕВ( С), випадковим чином витягує інший текст, позначений як С¢ , і посилає зашифровані тексти СС і С¢ А. ( Символи СС позначають карту, що належить Б , а символ С¢ - карту, видану А. Зашифрована карта, що залишилася, ігнорується.)
3. А розшифровує тексти СС і С¢. Результат розшифрування тексту С¢ позначає його карту, а розшифрування тексту СС, що позначається як С¢¢ , - карту Б. Текст С¢¢ повертається Б.
4. Б розшифровує текст С¢¢ і узнає свою карту.
Аналіз стійкості.
Після виконання протоколу складається наступна ситуація.
• Оскільки на першому кроці А тасує колоду, обидва гравці з однаковою імовірністю одержують одну з карт, що належать множині {M1, M2, M3}. Потрібно звернути увагу на те, що А прагне добре перетасувати колоду, щоб Б не одержав переваги. Отже, перша умова чесної роздачі виконана.
• Кожний з двох гравців після подвійного розшифрування дізнається свою карту, але не знає, яка карта дісталася супернику. Таким чином, друге правило чесної роздачі також виконане.
• Очевидно, що в протоколі врахована можливість шахрайства з боку гравців. Отже, третє правило чесної роздачі також виконане.
Виконання четвертого правила залежить від того, чи допускає криптосистема, використана в протоколі, чесну верифікацію закінченої гри. Шамір і його співавтори запропонували застосувати один з варіантів криптосистеми RSA, в якому обидві сторони до завершення гри зберігають в таємниці показники ступеня, використані при шифруванні і розшифруванні, а після її закінчення розкривають їх для перевірки.
Хай N - загальний модуль в криптосистемі RSA. А і Б знають розкладання числа N на множники. Позначимо через (еА, dA) показники ступенів, використані при шифруванні і розшифруванні А, а через (еВ, dВ) – показники, що вживаються Б. Знання розкладання числа N на прості множники дозволяє А (Б) знайти число еА по заданому числу dA (число еВ – по заданому числу dВ) за допомогою порівняння
еХ dХ = 1(mod j(N)) (2.5)
де символ X позначає гравця А або В, j(N) – функція Ейлера. Для користувача X одержуємо наступні формули.
ЕХ( М)=![]() ( mod N),
( mod N),
DХ( М)=![]() ( mod N).
( mod N).
Оскільки група RSA є комутативною, легко бачити, що умова (2.4) виконується. До завершення гри обидві сторони зберігають свої показники ступенів в таємниці. Таким чином, ніхто не може створити зашифрований текст, ідентичний тексту, створеному партнером. Це не дозволяє одному партнеру розкрити карти іншого партнера, одержавши зашифрований текст. Крім того, ніхто не може розшифрувати текст, створений іншим партнером. Таким чином, криптопротокол дійсно є достатньо стійким.
Очевидно, що після завершення гри обидві партії можуть розкрити свої показники ступенів і переконатися, що шифрування і розшифрування були виконані правильно. Отже, четверте правило чесної роздачі карт виконано.
2.3. Математичні моделі елементів криптографічних системРозглянемо моделі таких елементів криптосистем, як джерела повідомлень, ключової множини, шифру.
Моделі джерел відкритих текстів.
Детерміновані моделі.
Кожне джерело відкритого тексту (ДВП) характеризується:
1. одним або декількома мовами спілкування;
2. набором алфавітів, що використовуються;
3. визначеною тематикою повідомлень, що генеруються;
4. частотними характеристиками повідомлень.
ДВП породжує тексти у відповідності з правилами граматики деякої мови, що знаходить відображення і в статистичних характеристиках повідомлень. Наприклад у текстах на англійській мові за літерою q завжди йде літера r, в російських текстах літери ь і ъ ніколи не слідують за голосними буквами. Взагалі кожну мову і кожне ДВП можна характеризувати розбиттям множини усіх k-грам, k = 2, 3,…, на допустимі (що зустрічаються в яких-небудь текстах) і недозволені (що не зустрічаються в жодних текстах).
Розбиття множини усіх k-грам на допустимі та недозволені визначає детерміновану модель ДВП. В такій моделі відкритий текст розглядається як послідовність букв деякого алфавіту, що не містить недозволених k-грам. Можна помітити, що розподіл k-грам на допустимі і недозволені умовне, причина чому динамічність мови, її здатність до розвитку. Крім того, вказаний розподіл може мати індивідуальні особливості для кожного ДВП.
Імовірнісні моделі.
В імовірнісних моделях ДВП розглядається як джерело випадкових послідовностей.
Хай джерело генерує в алфавіті Zm текст кінцевої або нескінченної довжини. При цьому можна вважати, що джерело генерує кінцеву або нескінченну послідовність випадкових змінних х0, х1, …, хn-1, що приймають значення в Zm. Імовірність випадкового повідомлення (а0, а1,…, аn-1) визначається як імовірність такої послідовності подій:
Р(а0, а1,…, аn-1)= Р{ х0 = а0, х1 = а1,…, х n-1 = аn-1}.
Множина випадкових повідомлень утворює імовірнісний простір, якщо виконані умови:
1) Р(а0, а1,…, аn-1)³0 для будь-якого випадкового повідомлення
(а0, а1,…,аn-1);
2)![]() = 1;
= 1;
3) Для будь-якого повідомлення (ао, а1, …,аn-1) і будь-якого s > n
Р(ао, а1, …,аn-1) = ![]() ,
,
тобто імовірність будь-якого випадкового повідомлення довжини n є сума імовірностей усіх продовжень цього повідомлення до довжини s.
Текст, що породжується таким джерелом, є імовірнісним аналогом природної мови. Він володіє однаковими з мовою частотними характеристиками k-грам. Задаючи певний імовірнісний розподіл на множині відкритих текстів, задається відповідна модель ДВП.
Розглянемо таку імовірнісну модель ДВП, як стаціонарне джерело незалежних символів алфавіту.
У цій моделі передбачається, що імовірність повідомлень повністю визначається імовірністю використання окремих букв алфавіту у випадковому тексті:
Р(а0, а1,…, аn-1) = ![]()
де для всіх iÎ{0,1,…, n-1} і будь-якого aÎZm
P{xi = a}>0; ![]() = 1.
= 1.
Відкритий текст такого джерела є реалізацією послідовності незалежних випробувань в поліноміальній імовірнісній схемі з числом результатів, рівним т. Множина результатів взаємно-однозначний відповідає множині усіх символів алфавіту.
Приведемо списки букв високої частоти використання для деяких європейських мов (табл. 2.3.1).
Таблица 2.1 Частота букв в різних мовах
| Мова | Буква алфавіту/частота букви у текстах, % | |||||
| Англійська | Е/ 12,86 | Т/9,72 | А/7,96 | S/7,77 | N / 7,51 | К / 7,03 |
| Іспанська | Е/ 14,15 | А/ 12,90 | О / 8,84 | S / 7,64 | S/7,01 | К / 6,95 |
Подовження табл. 2.1
| Італійська | І/12,04 | Е/11,63 | А/11,12 | О/8,92 | N/7,68 | Т / 7,07 |
| Німецька | Е/ 19,18 | N1/ 10,20 | S/8,21 | S/7,07 | К/7,01 | Т/5,86 |
| Французьська | Е/ 17,76 | S / 8,23 | А/7,68 | N/7,61 | Т / 7,30 | I/7,23 |
| Російська | О / 11,0 | И/8,9 | Е/8,3 | А/7,9 | Н / 6,9 | Т/6,0 |
Ця модель дозволяє розділити букви алфавіту на класи високої, середньої і низької частоти використання. Модель будується для будь-якого ДВП з використанням відносно невеликої кількості матеріалу і зручна для практичного застосування. Наприклад, ця модель ефективно використовується при дешифруванні текстів, що захищаються шифром простої заміни.
В той же час деякі властивості даної моделі суперечать властивостям мов. Зокрема, згідно з цією моделлю будь-яка k-грама, k >1, має ненульову імовірність появи в повідомленні. Обмеженість моделі не дозволяє застосовувати її для дешифрування широкого класу криптосистем.
Імовірнісна модель ключової множини.
Імовірнісна модель ключової множини використовується крип-тоаналітіком для аналізу статистичних властивостей криптосистеми. Імовірнісна модель визначається, зокрема, завданням імовірнісного розподілу на ключовій множині, яка розглядається як простір елементарних подій. Кожному ключу kÎK ставиться у відповідність імовірність pk його використання для зашифрування або якогось конкретного, або випадкового відкритого тексту. При цьому ![]() .
.
У найбільш природній моделі, що часто приймається криптоаналітиком, передбачається, що ключі для шифрування вибираються незалежно від відкритих текстів і володіють добрими статистичними властивостями, тобто:
1) для чергового періоду експлуатації (сеансу, доби, і т. п.) кожен ключ вибирається випадково рівноймовірно з ключової множини K, тобто pk = 1/|K| для будь-якого kÎК;
2) при зміні ключів новий ключ вибирається незалежно від попередніх.
Імовірнісна модель шифру.
На основі відображень шифру, імовірнісних моделей відкритого тексту і множини ключів можна побудувати імовірнісну модель шифру. Позначимо деякі розподіли ймовірностей(р. й.):
Рвідкр – р. й. на множині відкритих текстів;
Ркл - р. й. на множині ключів;
Рш - р. й. на множині шифрованих текстів;
Рвідкр,к - сумісний р. й. на множині пар відкритих текстів і ключів;
Рвідкр,ш – сумісний р. й. на множині пар відкритих і шифрованих текстів;
Рвідкр/ш - умовний р. й. на множині відкритих текстів (при умові, що шифрований текст фіксований).
Хай а – відкритий текст, z – ключ, y – шифрований текст, Е(а, z) - криптограма, одержана в результаті шифрування відкритого тексту а на ключі z.
Звичайно вважають, що при шифруванні ключ z обирається незалежно від відкритого тексту а, тому
Рвідкр,к(a, z) = Рвідкр(a) Ркл(z).
Сумісні і умовні р. й. визначаються із формул:
Рш(y) = ![]() ,
,
Рвідкр,ш = ![]() ,
,
Рвідкр/ш = Рвідкр,ш(a,y)/ Рш(y),
де остання рівність витікає з визначення умовної імовірності і справедливо за умови Рш(y)>0.
Таким чином, маючи розподіли імовірності на множині відкритих текстів і ключів і знаючи сімейство шифру, можна у принципі обчислити як розподіл імовірності на множині шифртекстів, так і різні сумісні і умовні розподіли імовірності.
Використовуючи імовірнісну модель шифру, Шеннон вперше сформулював поняття абсолютно стійкого шифру.
2.4. Математична модель криптографічного протоколуЗ формальної точки зору абстрактний аутентифікації протокол описується функцією P, що має поліноміальну складність і наступні аргументи.
1k – Параметр безпеки k Î N.
i – Ідентифікатор користувача i Î I , що виконує дану частину протоколу. Називатимемо цього користувача "власником". Множина I складається з користувачів, що володіють одним і тим же довготривалим ключем.
j – Ідентифікатор партнера, з яким спілкується власник; j Î I.
К – Довготривалий симетричний ключ (тобто секретна вхідна інформація). У двосторонньому протоколі симетричний ключ К належить як власнику, так і його партнеру.
сonv – Попередні повідомлення – conv (від англ.: conversation ), що є рядком бітів. Цей рядок збільшується у міру виконання протоколу, причому новий рядок приписується до старого.
r – Випадковий аргумент власника – можна вважати число r одноразовим випадковим числом, що генерується власником.
Оскільки P(1k,i,j,K,conv,r) має поліноміальну складність, залежну від розміру аргументів (відзначимо, що розмір параметра k рівний 1k), можна вважати, що аргументи K і r мають розмір k, а розмір аргументів i, j і conv поліноміальнo залежить від параметра k.
Значеннями функції P(1k,i,j,K,conv,r) є три числа.
m – Наступне повідомлення, що підлягає відправці, - m Î {0,1}* ![]() {"повідомлень немає"}. Це – відкрите повідомлення, що підлягає відправці адресату через відкриту мережу.
{"повідомлень немає"}. Це – відкрите повідомлення, що підлягає відправці адресату через відкриту мережу.
δ – Рішення користувача – δ Î { Прийняти, Відмовити, Не приймати рішення}. Користувач вирішує, прийняти або відкинути ідентифікатор партнера по переговорах, або не ухвалювати рішення взагалі. Прийняття ідентифікатора, як правило, відкладається до завершення протоколу, а відхилити його можна у будь-який момент. Якщо користувач ухвалює яке-небудь певне рішення, значення δ більше не змінюється.
α – Закритий результат, обчислений власником, - α Î {0,1}* ![]() {"результату немає"}. Можна вважати, що закритим результатом, обчисленим власником при сприятливому результаті протоколу, є узгоджений сеансовий ключ.
{"результату немає"}. Можна вважати, що закритим результатом, обчисленим власником при сприятливому результаті протоколу, є узгоджений сеансовий ключ.
Діалог між цими користувачами є послідовністю впорядкованих в часі повідомлень, що посилаються ними в мережу, і одержуваних на них відповідей. Хай t1 < t2 < …<tR ,(де R – деяке позитивне ціле число) – моменти часу, в які користувач і посилає повідомлення. Діалог можна позначити таким чином.
conv =( t1, m1, m’1), (t2, m2, m’2),…, (tR, mR, m’R).
Цей запис означає, що у момент t1 користувач і одержує запит m1 і посилає у відповідь повідомлення m’1. Потім у момент t1> t2 користувач і одержує запит m2 і посилає у відповідь повідомлення m’2 і так далі, поки у момент tR він не одержить запит mR і пошле у відповідь повідомлення m’R.
Нагадаю, що в даній моделі користувач будь-який запит повинен вважати повідомленням від Зловмисника, поки в якийсь момент tR він не прийме позитивне рішення. Зручно припустити, що діалог починає Зловмисник. Отже, якщо m1 = “”, називатимемо користувача і ініціатором діалогу, інакше – відповідачем.
Хай
conv = (t0, “”, m1), (t2, m’1, m2), (t4, m’2, m3),…, (t2t-2, m’t-1, mt)
позначає діалог користувача і . Користувач j веде діалог conv', узгоджений з діалогом conv, якщо існує послідовність моментів часу t0 < t1 < t2 …<tR, така що
conv’ = (t1, m1, m’1), (t3, m2, m’2), (t5, m3, m’3),…, (t2t-2, mt, m’t),
де рядок m’t означає "немає повідомлень".
Якщо користувачі i і j ведуть узгоджені діалоги, то Зловмисник не в змозі організувати небезпечну атаку і вимушений грати роль нешкідливого супротивника.
Протокол П(1k,{A, В}) є стійким протоколом аутентифікації, що виконується користувачами А і В, якщо обидва користувача приймають позитивне рішення тоді і тільки тоді, коли вони ведуть узгоджені діалоги, причому імовірність протилежної близька до нуля.
Якщо протокол є стійким, то з існування узгоджених діалогів безпосередньо слідують позитивні рішення користувачів. Довести зворотне твердження, тобто що з позитивних рішень виходить існування узгоджених діалогів, набагато складніше. Отже, метою атаки на протокол є отримання позитивних рішень, коли узгоджених діалогів не існує. Таким чином, коректнішим є наступне визначення стійкості протоколу.
Протокол П(1k,{A, В}) виявляється стійким протоколом аутентифікації, що виконується користувачами А і В, якщо імовірність виграшу Зловмисника дуже мала. Тут виграш Зловмисника означає, що обидва користувача приймають позитивне рішення, хоча між ними немає узгоджених діалогів.
Висновки
Таким чином, в цьому розділі ми визначили такі важливі поняття криптографії, як стійкість шифрсистем, стійкості криптографічних протоколів, причини ії пониження, привели приклад достатньо стійкого криптопротоколу, розглянули математичні моделі джерела повідомлень, ключової множини, шифру і, нарешті, крипторотоколу. Це все було зроблено для того, щоб полегшати формалізування опису протоколів для доказування їхньої стійкості.
Розділ 3. Оцінка стійкості криптографічних протоколів на основі імовірнісних моделей 3.1. Методика оцінки стійкості
Формальний доказ стійкості в рамках обчислювальної моделі складається з трьох етапів.
1. Формальна поведінка учасників протоколу і атакуючого алгоритму: моделювання, як правило, здійснюється за допомогою атакуючої гри, в якій беруть участь атакуючий алгоритм і об'єкт атаки.
2. Формальне визначення стійкості: перемога атакуючого алгоритму в атакуючій грі звичайно виражається через (значущу) ймовірність і оцінку (розумної) тимчасової складності.
3. Формальна демонстрація існування поліноміальної редукції, що зводить атаку до рішення задачі, що важко вирішується, як правило, має вид математичної теореми.
3.2. Приклади доказу стійкості деяких протоколів на основі їх імовірнісних моделейАналіз стійкості будемо проводити на основі імовірнісної моделі протоколів з нульовим розголошенням.
Одне з основних завдань криптографії представляє собою двосторонню інтерактивну гру, в якій один учасник (сторона, що доводить) доказує іншому учаснику (стороні, що перевіряє) істинність твердження, не розкриваючи суті доказу. В цьому випадку сторона, що перевіряє не може самостійно оцінити істинність твердження, оскільки йому невідома інформація, яка доступна стороні, що доводить. Ця гра називається протоколом (системою) інтерактивного доказування або ІР-протоколом. Доказування, здійснюване ІР-протоколом, можна назвати «секретним доказуванням». Секретність цього доказу полягає в тому, що по-перше, сторона, що перевіряє, переконавшись в істинності доказуваного твердження, не здатна самостійно повторити доказ, і, по-друге, після завершення протоколу ніхто із сторонніх не здатний зрозуміти жодного повідомлення, якими обмінювалися сторона, що перевіряє і сторони, що доводить.
Уявимо собі, що твердження, яке необхідно довести, не розкриваючи сутності доказу, є рішенням якої-небудь відомої невирішеної математичної задачі. В цьому випадку доказуючи сторона побоюючись плагіату, може побажати приховати технічні деталі доказу від потенційно нечесного рецензента. Для цього вона повинна провести «секретний» доказ, переконавши рецензента (що грає роль сторони, що перевіряє в ІР-протоколі) в коректності висновків, не даючи ніякої додаткової інформації.
У багатьох реальних системах існують набагато більш серйозні підстави для проведення «секретних» доказів. Як правило, ІР-протоколи застосовуються для аутентифікації сутностей. На відміну від звичайних протоколів аутентифікації, в яких користувачі ставлять цифрові підписи, в ІР-протоколі сторона, що доводить не бажає, щоб повідомлення стали доступними кому-небудь, окрім сторони, що перевіряє, і виконує «секретну» аутентифікацію. Крім того, ІР-протоколи часто застосовуються для того, щоб довести, що частина прихованої інформації має певну структуру. Це необхідно в деяких секретних системах (наприклад, при проведенні електронних аукціонів), в яких прихований номер (лот) повинен знаходитися в допустимому діапазоні (наприклад, необхідно довести, що х > у без розкриття значень Ек(х) і Ек(у), що є пропозиціями ціни).
Розглядаючи ІР-протоколи, необхідно вивчити два питання.
Питання 1. Скільки інформації одержить сторона, що перевіряє в ході інтерактивного доказу?
Питання 2. Скільки раундів повинна виконати сторона, що доводить, щоб переконати сторону, що перевіряє?
Ідеальною відповіддю на перше питання був би "аніскільки", або "нуль". ІР-протокол, що володіє такою властивістю, називається протоколом з нульовим розголошуванням або ZК-протоколом (zero-knowledge). Друге питання важливе не тільки для практичних застосувань, але і для теорії обчислювальної складності, оскільки рішення цієї проблеми пов'язане з отриманням нижчої оцінки складності.
Розглянемо обчислювальну модель інтерактивної системи доказу, яку запропонували Голдвассеср, Мікаплі і Раков. Позначимо основну модель протоколу інтерактивного доказу через (Р, V), де Р – сторона, що доводить (prover), а V – сторона, що перевіряє (verifier). Як правило, протокол (Р, V) призначений для перевірки приналежності певного речення мові, заданій над алфавітом {0, 1}.
Хай L – мова над алфавітом {0,1}. Сторони Р і V одержують зразок хÎL, що є загальними вхідними даними. Доказ приналежності зразка позначається як (Р, V)(х). Обидві сторони протоколу пов’язані каналом зв’язку, через який вони обмінюються інформацією.
a1, b1, a2, b2,…, al, bl.
Ця послідовність повідомлень називається стенограмою доказу. У стенограмі доказу дані, що передаються користувачем Р, називаються стенограмою сторони, що доводить. Вони чергуються з даними, що передаються користувачем V, які називаються стенограмою сторони, що перевіряє. Як загальна довжина стенограми доказу l , так і довжина кожної стенограми |аі|, |bi| (i = 1,2...,l) обмежена поліномом, що залежить від параметра |х|. Доказ приналежності зразка (Р, V)(х) мові L також повинен бути обмежений поліномом, який залежить від об'єму вхідних даних |х| .
Результат роботи протоколу записується у вигляді
(Р, V)(х) Î { Прийняти, Відхилити}.
Ці два значення означають, що сторона, що перевіряє або підтверджує, або спростовує твердження хÎL , висловлене стороною, що доводить Р. Оскільки система (Р, V) є імовірнісною, при кожному х результат (Р, V)(х) є випадковою величиною, залежною від загальних вхідних даних х, закритих вхідних даних (рrivate input) користувача Р і деяких випадкових вхідних даних (random input), загальних для користувачів Р і V. Більш того, елементи стенограми доказу також є випадковими величинами.
Оскільки протокол (Р, V) є двосторонньою грою, природно припустити, що кожна сторона прагне одержати додаткову перевагу. З одного боку, сторона, що доводить, Р повинна бути зацікавлена в результаті (Р, V)(х) Прийняти, навіть якщо хÏL. Сторона, що доводить, яка керується такою шахрайською стратегією, позначається як Р’. З іншого боку, сторона, що перевіряє V повинна бути зацікавлена в розкритті інформації про закриті вхідні дані гравця Р. Сторона, що перевіряє, яка притримується такої нечесної стратегії позначається як V.
Дамо визначення протоколу інтерактивного доказу.
Хай L - мова, задана над алфавітом {0,1}. IР-протокол (Р,V) називається системою інтерактивного доказу для мови L, якщо
Ргоb[(Р, V)(х) = Прийняти | х Î L] ³ e, (3.1)
Ргоb[(Р’, V)(х) = Прийняти | х Ï L] £ d, (3.2)
де числа e і d є константами, що задовольняють умовам
e Î![]() , d Î
, d Î![]() .
.
Імовірнісний простір складається зі всіх вхідних значень протоколу (Р, V) і всіх випадкових вхідних даних користувачів Р і V.
Оцінка (3.1) характеризує повноту протоколу (Р,V). Величина e називається імовірністю повноти протоколу (Р, V). Це означає, що якщо хÎL, то сторона, що перевіряє, V приймає припущення х з імовірністю, яка не менше величини e.
Оцінка (3.2) характеризує несуперечність протоколу (Р,V). Величина d називається імовірністю суперечності протоколу (Р,V). Це означає, що якщо хÏL, то сторона, що перевіряє, V приймає припущення х з імовірністю, що не перевищує величини d.
Оцінку імовірності повноти (відповідно суперечності) можна збільшити (відповідно зменшити), наблизивши її скільки завгодно близько до одиниці (відповідно до нуля), послідовно і незалежно повторюючи протокол (Р,V) поліноміально обмежену кількість раз (залежно від розміру вхідного речення). В цьому випадку сторона, що перевіряє, V ухвалює рішення шляхом голосування.
Розглянемо введені поняття на прикладі протоколу інтерактивного доказу приналежності підгрупі (Протокол 3.1) .
Загальні вхідні дані:
1. ƒ: однонаправлена функція, визначена в групі Zn і задовольняюча гомоморфній умові:
"х, уÎ Zn : ƒ (х + у) = ƒ (х) ƒ (у).
2. Х = ƒ (z) для деякого zÎ Zn .
Закриті вхідні дані сторони А:
z < n.
Висновок сторони Б:
Х Î á ƒ (1)ñ, тобто елемент Х породжується елементом ƒ (1).
Наступні кроки виконуються m раз.
1. А генерує число k Î Zn, знаходить число Сommit ¬ƒ(k) і посилає його Б.
Похожие работы
... захисту необхідно виявити можливі погрози безпеці інформації, оцінити їх наслідки, визначити необхідні заходи і засоби захисту і оцінити їх ефективність. [25] 1.3 Криптографічні методи захисту інформації Криптографічний захист інформації — вид захисту інформації, що реалізується за допомогою перетворень інформації з використанням спеціальних даних (ключових даних) з метою приховування (або ...
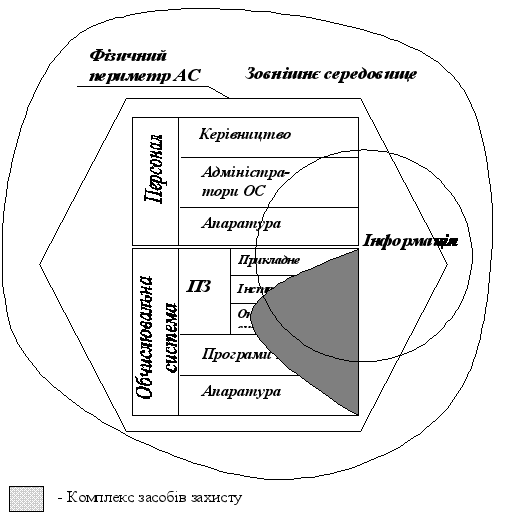
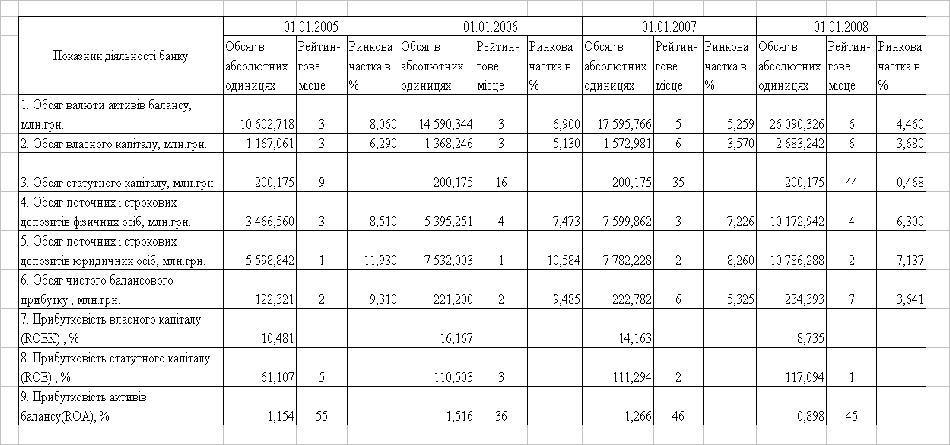
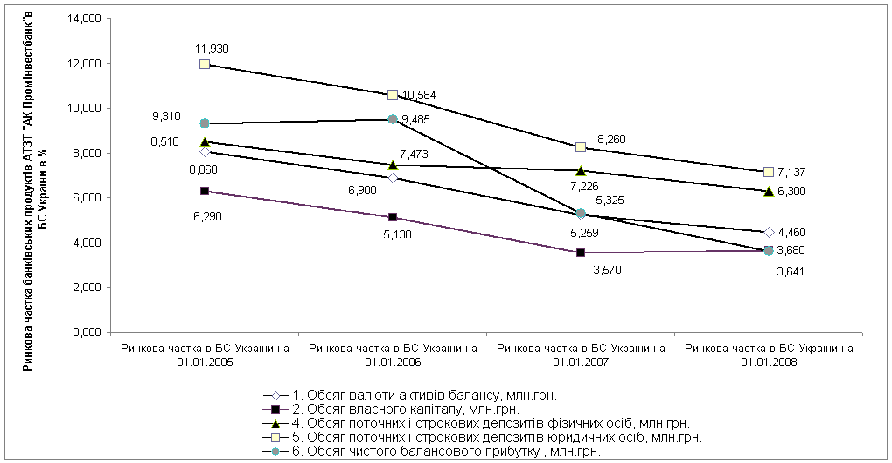
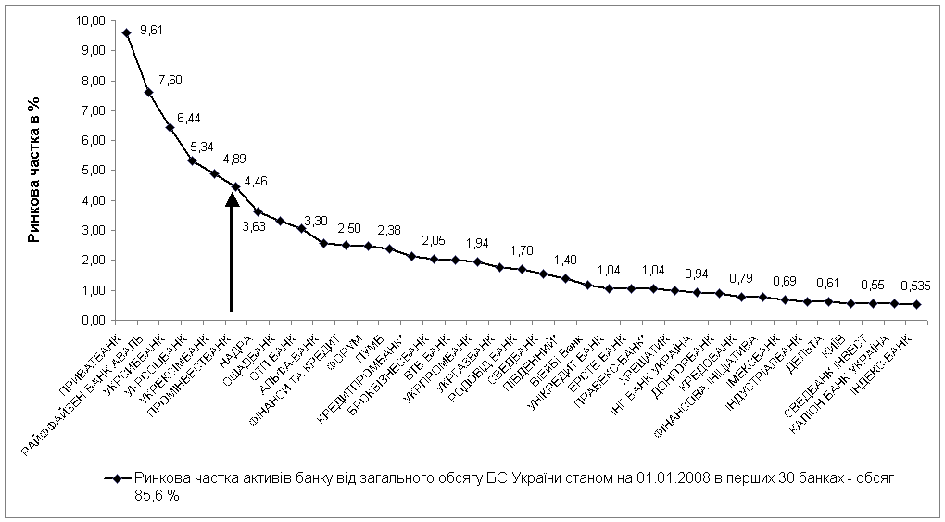
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
... передбаченою. 3. Генерація гамми не повинна бути дуже трудомісткою. Слід зазначити, що алгоритми криптосистем з відкритим ключем (СВК) можна використовувати за трьома напрямками: 1. Як самостійні засоби захисту даних, що передаються чи зберігаються. 2. Як засіб для розподілу ключів. Алгоритми СВК більш трудомісткі, ніж традиційні криптосистеми. Обмін великими інформаційними потоками здійснюють ...
... ональних інтересів та безпеку інформаційного простору. Підсумки: В цьому розділі ми з’ясували, які саме зміни всередині урядових організацій, в їх структурі, функціях і методах роботи ініціює запровадження електронного уряду. А саме: відбувається перенесення акцентів з вертикальних на горизонтальні зв’язки всередині уряду, між різними його підрозділами і гілками влади. За рахунок створення внутрі ...


0 комментариев