Навигация
Введение
Глава 1. Представление данных в цифровых автоматах (ЦА)
1.1 Представление чисел в позиционных системах счисления (ПСС)
1.2 Формы представления данных в ЦА
1.3 Выполнение арифметических операций с целыми числами, представленными в машинных кодах
1.4 Выполнение логических операций с целыми числами, представленными в машинных кодах
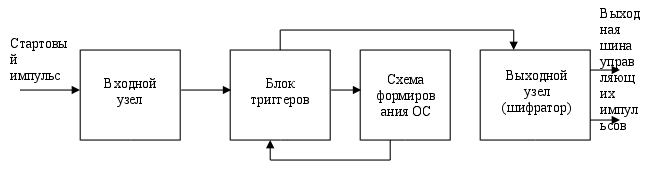
Глава 2. Методы контроля работы ЦА
2.1. Корректирующая способность кодов
2.2 Метод четности / нечетности. Коды Хеминга
2.3 Контроль по модулю
Глава 3. Построение алгоритма реализации численного метода «быстрой сортировки»
3.1 Математическое описание метода
3.2 Таблица используемых переменных
Список используемых источников
Приложение 1. Блок-схема алгоритма
Введение
В своей курсовой работе я ставлю следующие задачи:
– научиться представлять данные в ЦА;
– изучить методы контроля работы ЦА и научиться строить код Хемминга;
– изучить реализацию алгоритма численного метода «быстрой сортировки» и построить его блок-схему.
Глава 1. Представление данных в цифровых автоматах (ЦА)
1.3 Представление чисел в позиционных системах счисления (ПСС)
Система счисления – это совокупность символов и правил их записи, необходимых для записи чисел.
В позиционной системе счисления вес символа зависит от позиции в которой расположен символ. Например, число 222 – первый символ этого числа имеет вес 200, второй – 20, третий – 2.
Основной характеристикой ПСС является основание. Основание ПСС – это количество символов данной системы счисления, которые используются при составлении чисел. В зависимости от основания ПСС существует четыре основных системы счисления: двоичная, восьмеричная, десятеричная и шестнадцатеричная. Все эти системы счисления используются в ЦА и каждая имеет свои основные функции. Например, числа, записанные в двоичной системе счисления, используются в ЦА для операций производимых процессором: запись, считывание, сложение и т.д.; числа в шестнадцатеричной системе счисления – для адресации ячеек памяти.
Перевод чисел из одной ПСС в другую
При переводе чисел из десятичной системы счисления в систему с основанием P обычно используют следующий алгоритм:
1) если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;
2) если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P.
Перевод числа из системы счисления с основанием P1 в систему счисления с основанием P2, можно выполнить по такому же алгоритму, но все вычисления нужно проводить в системе счисления с основанием P1. Второй способ перевести число можно в два этапа: переведя это число в десятеричную систему счисления, а затем из десятеричной в систему счисления с основанием P2.
Чтобы перевести число из системы счисления с основанием P
в десятичную систему счисления, нужно найти сумму произведений содержимого разряда на вес этого разряда в системе счисления с основанием P. Где разряд – номер позиции в числе, нумеруются справа налево, начиная с нуля; вес разряда – число, равное основанию системы счисления в степени номера разряда.
Чтобы перевести число из двоичной системы счисления
в восьмеричную (шестнадцатеричную) систему счисления, нужно разбить число на тройки (четверки) цифр, в случае необходимости следует дополнить целую и дробную части числа нулями (целую слева, дробную справа). Затем заменить полученные группы цифр соответствующими им восьмеричными (шестнадцатеричными) цифрами. Например, число 11010010.102 нужно перевести в восьмеричную систему счисления. Разобьем число на тройки цифр: 011 010 010. 100 , заменим тройки цифр на соответствующими им восьмеричными цифрами. Получим 11010010.102 = 322.48
Чтобы перевести число из восьмеричной (шестнадцатеричной) системы счисления в двоичную систему счисления, нужно заменить каждую цифру числа соответствующими им тройками (четверками) двоичных цифр.
Задание. Осуществить перевод числа (А+В), представленного в 10-ой системе из одной системы счисления в другие, по схеме рисунка.
![]()
![]()
![]()
![]() (А+В)10
(А+В)10
|
|
|
|
|
|
|
|
|
|
|
![]()
|
Решение.
А+В=307+6.6=313.610
313.610 = ( )2
Сначала переводим целую часть числа, делим на основание 2:
313/2=156 остаток – 1;
156/2=78 остаток – 0;
78/2=39 остаток – 0;
39/2=19 остаток – 1;
19/2=8 остаток – 1;
9/2=4 остаток – 1;
4/2=4 остаток – 0;
2/2=1 остаток – 0;
Дальше делить нельзя, поэтому собираем все остатки, начиная с конца и учитываем конечный результат от деления т.е. 2/2=1. Получим 31310=1001110012
Теперь переводим дробную часть числа, умножаем на основание 2:
| * | 6 | * | 2 | * | 4 | * | 8 | ||||
| 2 | 2 | 2 | 2 | ||||||||
| 1 | 2 | 0 | 4 | 0 | 8 | 1 | 6 |
Получим 0.610 = 0.10012 , значит,
31310 » 100111001.10012
100111001.10012 = ( )8
Разобьем число на тройки цифр: 100 111 001. 100 100 , заменим тройки цифр на соответствующими им восьмеричными цифрами т.е. 1002=48 ; 1112=78 ; 0012=18 . Получим 100111001.10012 =471.448
100111001.10012 = ( )10
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | . | 1 | 0 | 0 | 1 | Число |
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 | Разряды числа |
100111001.10012 = 1*2-4 + 1*2-1 + 1*20 + 1*23 + 1*24 + 1*25 + 1*28 =
= 0.0652 + 0.5 + 1 + 8 + 16 + 32 + 256 = 313.565210 » 313.610
100111001.10012 = ( )16
Разобьем число на четверки цифр: 0001 0011 1001. 1001 , заменим четверки цифр на соответствующими им шестнадцатеричными цифрами т.е. 00012=116; 00112=316 ; 10012=916 . Получим 100111001.10012 =139.916
313.610 = ( )8
Сначала переводим целую часть числа, делим на основание 8:
313/8=39 остаток – 1;
39/8=4 остаток – 7.
Получим 31310=4718
Теперь переводим дробную часть числа, умножаем на основание 8:
| * | 6 | * | 8 | * | 4 | * | 2 | ||||
| 8 | 8 | 8 | 8 | ||||||||
| 4 | 8 | 6 | 4 | 3 | 2 | 1 | 6 |
Получим 0.610 = 0.46318 , значит,
31310 » 471.46318
471.46318 = ( )2
Каждый символ числа 471.46318 запишем в двоичной системе счисления: 48=1002 ; 78=1112 ; 18=0012 ; 68=1102 ; 38=0112 .
Получим 471.46318 = 100111001.1001100110012
471.46318 = ( )10
| 4 | 7 | 1 | . | 4 | 6 | 3 | 1 | Число |
| 2 | 1 | 0 | -1 | -2 | -3 | -4 | Разряды числа |
471.46318 = 1*8-4 + 3*8-3 + 6*8-2 + 4*8-1 + 1*80 + 7*81 + 4*82 =
= 0.0002 + 0.0058 + 0.0937 + 0.5 + 1 + 56 + 256 = 313.599710 » 313.610
471.46318 = ( )16
Перевод числа из восьмеричной системы счисления в шестнадцатеричную проведем в два этапа: сначала переведем число в десятеричную систему счисления, затем из десятеричной в шестнадцатеричную. Перевод числа 471.46318 в десятеричную систему счисления уже осуществлен выше: 471.46318 = 313.610 . Далее переведем 313.610 в шестнадцатеричную систему счисления:
313.610 = ( )16
Сначала переводим целую часть числа, делим на основание 16:
313/16=19 остаток – 9;
19/16=1 остаток – 3.
Получим 31310=13916
Теперь переводим дробную часть числа, умножаем на основание 16:
| * | 6 | * | 6 | ||
| 16 | 16 | ||||
| 9 | 6 | 9 | 6 |
Получим 0.610 = 0.9916 , значит,
31310 » 139.9916
139.9916 = ( )2
Каждый символ числа 139.9916 запишем в двоичной системе счисления: 116=00012 ; 316=00112 ; 916=10012 .
Получим 139.9916 = 100111001.100110012
139.9916 = ( )8
Перевод числа из шестнадцатеричной системы счисления в восьмеричную будем выполнять в один этап, делая все вычисления в шестнадцатеричной системе счисления.
Сначала переводим целую часть числа, делим на основание 8:
| 139 | 8 | ||
| 100 | 27 | ||
| – | 39 | ||
| 38 | |||
| 1 | |||
| 27 | 8 |
| 20 | 4 |
| 7 |
Дальше делить нельзя, поэтому собираем все остатки, начиная с конца и учитываем конечный результат от деления т.е. 20/8=4. Получим 13916 = 4718
Теперь переводим дробную часть числа, умножаем на основание 8:
| * | 99 | * | С8 | * | 40 | |||
| 8 | 8 | 8 | ||||||
| 4 | С8 | 6 | 40 | 2 | 00 |
Получим 0.9916 = 0.46208 , значит,
139.9916 » 471.46208
139.9916 = ( )10
1 | 3 | 9 | . | 9 | 9 | Число |
| 2 | 1 | 0 | -1 | -2 | Разряды числа |
139.9916 = 9*16-2 + 9*16-1 + 9*160 + 3*161 + 1*162 = 0.0351 + 0.5625 + 9 + 48 + 256 = 313.597610 » 313.610
Выполнение арифметических операций над числами, представленными в ПСС
Операции над числами в двоичной, восьмеричной, шестнадцатеричной системе счисления выполняются по тем же правилам, что и арифметические операции над числами в десятеричной системе счисления.
Задание
А) Сложить числа (А)16 и (В)16
(А)10 = 30710 = 13316 (В)10 = 6.610 = 6.9916
| + | 133.00 |
| 6.99 | |
| 139.99 |
Б) Вычесть из числа (А)8 число (В)8
(А)10 = 30710 = 4638 (В)10 = 6.610 = 6.468
| – | 463.00 |
| 6.46 | |
| 454.31 |
В) Умножить числа (С)2 и (В)2
(С)10 = 9110 = 10110112 (В)10 = 6.610 = 110.10012
| * | 1011011 | |
| 110.1001 | ||
| 1011011 | ||
| + 1011011000 | ||
| 101101100000 | ||
| 1011011000000 | ||
| 1001010101.0011 | ||
В) Разделить число (С)2 на (В)2
(С)10 = 9110 = 10110112 (В)10 = 6.610 = 110.12
| 1011011 | 110.1 | Þ |
| 10110110 | 1101 | ||
| 01101 | 1110.0 | ||
| 010011 | |||
| 001101 | |||
| 0001101 | |||
| 0001101 | |||
| 0000000 | |||
Похожие работы
... в народном хозяйстве. Специальная часть. 3. 1. Определение задачи. Из задания на курсовое проектирование определим суть задачи: для некоторого синхронного цифрового автомата необходимо спроектировать устройство управления на основе жёсткой логики, которое в соответствии с заданными кодами микрокоманд формирует на выходной десятиразрядной шине управляющую последовательность цифровых сигналов. 3. ...
... . Функционирование цифрового автомата проверить на примере массива данных состоящей из шести элементов. Элементы массива A=5, B=2, x=2. Функционирование цифрового автомата представлено в табл.4 R1 R R3 R4 Sm1 Sm2 Выполняемая операция 0011 y1:R1ßx 0011 y2:R2ßB 0101 ...
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...
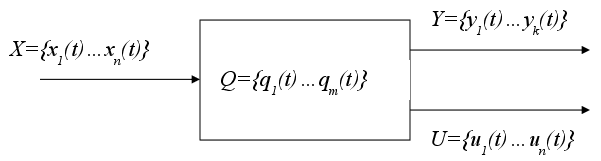
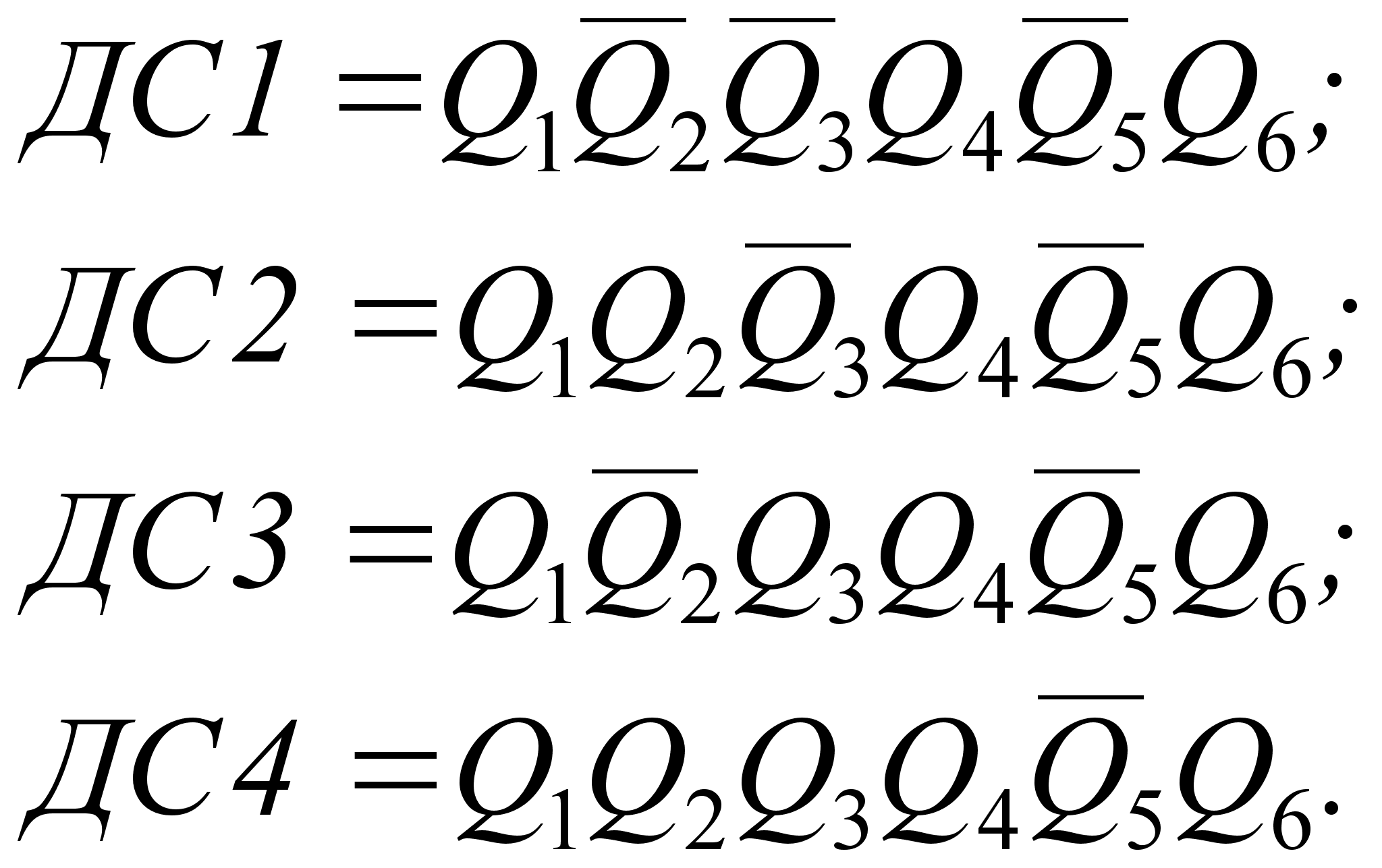
0 комментариев