Навигация
Формы представления данных в ЦА
1.2 Формы представления данных в ЦА
Кодирование и формы представления чисел в ЦА
Представление чисел в машинных кодах для выполнения арифметических операций
Прямой код – это двоичный код числа, записанный в разрядной сетке, в старшем разряде которого указывается знак числа.
Для положительных чисел прямой код числа совпадает с обратным и дополнительном кодом т.е. [A]пр = [A]обр = [A]доп .
В противном случае, когда число отрицательное:
– обратный код получается из прямого, путем инверсии всех разрядов, за исключением знакового;
– дополнительный код получается путем прибавления единицы к обратному коду т.е. [A]доп = 1 + [A]обр .
Модифицированный обратный (дополнительный) код – аналог обратного (дополнительного) кода, с той лишь разницей, что на знак выделяются два старших разряда.
Задание. Числа А, –А, С и –С представить в прямом, обратном, дополнительном, модифицированном обратном и модифицированном дополнительном кодах.
А = 30710 = 1001100112 С = 9110 = 10110112
[A]пр = [A]об = [A]доп = 0|000000100110011
[A]мод.об = 00|00000100110011
[A]мод.доп = 00|00000100110011
[–A]пр = 1|000000100110011
[–A]об = 1|111111011001100
[–A]мод.об = 11|11111011001100
[–A]доп = 1|111111011001100+1 = 1|111111011001101
[–A]мод.доп = 11|11111011001100+1 = 11|11111011001101
[C]пр = [C]об = [C]доп = 0|000000001011011
[C]мод.об = 00|00000001011011
[C]мод.доп = 00|00000001011011
[–C]пр = 1|000000001011011
[–C]об = 1|111111110100100
[–C]мод.об = 11|11111110100100
[–C]доп = 1|111111110100100+1 = 1|111111110100101
[–C]мод.доп = 11|11111110100100+1 = 11|11111110100101
Представление чисел в формате с фиксированной запятой
Для чисел, представленных в формате с фиксированной запятой, предварительно определяется место запятой между разрядами, поэтому число может быть определено только в определенном диапазоне. Если рассматривать два числа, у которых место положения различны, то числа выравниваются по младшему разряду. Для этого все числа заносимые в ЦА предварительно умножаются на маштабный коэффициент.
Например:
111.101 * 24 = 1111010 – целый вид;
111.101 * 2–3 = 0.111101 – дробный вид,
где 24 и 2–3 – маштабный коэффициент.
Задание. Числа A, –A, B и –B представить в формате с фиксированной точкой (в 16-ти разрядах). При этом числа A и B привести к целому виду, а –A и –B к дробному с 4-мя знаками после запятой.
А = 30710 = 1001100112
A = 0000000100110011 – целый вид;
A = 100110011*2–4 = 000000010011.0011 – дробный вид.
В = 6.610 = 110.12
B = 110.1*21 = 0000000000001101 – целый вид;
B = 110.1*2–3 = 000000000000.1101 – дробный вид.
Представление чисел в формате с плавающей запятой
Любое число N в системе счисления с основанием q можно записать в виде N=M*qp, где M называется мантиссой числа, а p – порядком. Такой способ записи чисел называется представлением с плавающей точкой.
Мантисса должна быть правильной дробью, первая цифра дробной части которой отлична от нуля: M из диапазона [0.1; 1).
Такое, наиболее выгодное для компьютера, представление вещественных чисел называется нормализованным.
Мантиссу и порядок q-ичного числа принято записывать в системе с основанием q, а само основание – в десятичной системе.
При хранении числа с плавающей точкой отводятся разряды для мантиссы, порядка, знака числа и знака порядка:
| … |
| … |
![]()
![]()
![]()
|
|
|
Например: 753.15 = 0.75315*103.
Задание. Числа A, –A, B и –B представить в формате с плавающей точкой.
А = 307 = 0.307*103
В = 6.6 =0.66*101
Кодирование и формат представления символьной информации
В большинстве первых компьютеров использовался семибитный код КОИ-7 (код обмена информацией, семизначный). В таком коде можно было закодировать 27=128 символов. Но с развитием техники это стало довольно неудобно.
Новый код был уже восьмибитным и основывался на американском стандартном коде обмена информацией ASCII (American Standard Code for Information Interchange). В восьмибитном коде можно закодировать уже 28=256 символов. Этого вполне хватает чтобы без всяких проблем использовать в тексте большие и маленькие буквы русского и латинского алфавитов, знаки препинания, цифры, специальные символы.
С недавнего времени был предложен новый стандарт символьного кодирования UNICODE. Шестнадцать разрядов позволяют обеспечить уникальные коды для 216=65536 различных символов – этого поля достаточно для размещения в одной таблице символов большинства языков планеты.
Задание. Используя таблицу Windows 12.51, закодировать свои: фамилию и имя (записанные на русском и английском языках). Вписать их в разрядную сетку.
| Буква | Десятиричный код | Двоичный код | Буква | Десятиричный код | Двоичный код | |
| Ш | 216 | 11011000 | S | 83 | 1010011 | |
| а | 224 | 11100000 | h | 104 | 1101000 | |
| б | 225 | 11100001 | a | 97 | 1100001 | |
| а | 224 | 11100000 | b | 98 | 1100010 | |
| р | 240 | 11110000 | a | 97 | 1100001 | |
| о | 238 | 11101110 | r | 114 | 1110010 | |
| в | 226 | 11100010 | o | 111 | 1101111 | |
| v | 118 | 1110110 | ||||
| П | 207 | 11001111 | ||||
| а | 224 | 11100000 | P | 80 | 1010000 | |
| в | 226 | 11100010 | a | 97 | 1100001 | |
| е | 229 | 11100101 | v | 118 | 1110110 | |
| л | 235 | 11101011 | e | 101 | 1100101 | |
| l | 108 | 1101100 |
Похожие работы
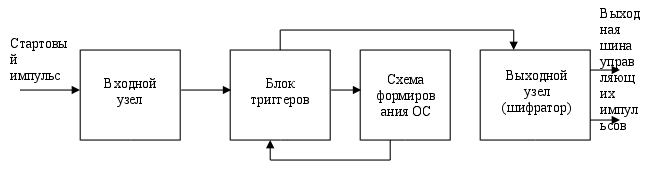
... в народном хозяйстве. Специальная часть. 3. 1. Определение задачи. Из задания на курсовое проектирование определим суть задачи: для некоторого синхронного цифрового автомата необходимо спроектировать устройство управления на основе жёсткой логики, которое в соответствии с заданными кодами микрокоманд формирует на выходной десятиразрядной шине управляющую последовательность цифровых сигналов. 3. ...
... . Функционирование цифрового автомата проверить на примере массива данных состоящей из шести элементов. Элементы массива A=5, B=2, x=2. Функционирование цифрового автомата представлено в табл.4 R1 R R3 R4 Sm1 Sm2 Выполняемая операция 0011 y1:R1ßx 0011 y2:R2ßB 0101 ...
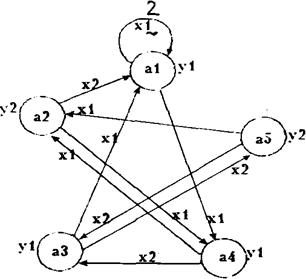
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...
0 комментариев