Навигация
Выполнение арифметических операций с целыми числами, представленными в машинных кодах
1.3 Выполнение арифметических операций с целыми числами, представленными в машинных кодах
Арифметические операции с целыми числами, представленными в машинных кодах, выполняются только операцией сложения. Т.е. операция разности, заменяется операцией сложения, операция произведения также заменяется операцией сложения.
Например, вычислить: А + B, A – B, –A – B. Пусть А=16010, B=4510.
[A]доп = 0|000000010100000
[–A]доп = 1|111111101100000
[B]доп = 0|000000000101101
[–B]доп = 1|111111111010011
| А + B | A – B | –A – B | |||||
| + | 0|000000010100000 | + | 0|000000010100000 | + | 1|111111101100000 | ||
| 0|000000000101101 | 1|111111111010011 | 1|111111111010011 | |||||
| 0|000000011001101 | 0|000000001110011 | 1|111111100110011 |
Задание. Произвести сложение чисел, представленных в машинных кодах: A+C; –A+C; A+(– C); –A+(– C).
A = 30710 =1001100112 С = 9110 = 10110112
[A]доп = 0|000000100110011
[–A]доп = 1|111111011001101
[C]доп = 0|000000001011011
[–C]доп = 1|111111110100101
| А + C | –A + C | |||
| + | 0|000000100110011 | + | 1|111111011001101 | |
| 0|000000001011011 | 0|000000001011011 | |||
| 0|000000110001110 | 1|111111100101000 | |||
| А + (– C) | –A + (– C) | |||
| + | 0|000000100110011 | + | 1|111111011001101 | |
| 1|111111110100101 | 1|111111110100101 | |||
| 0|000000011011000 | 1|111111001110010 |
1.4 Выполнение логических операций с целыми числами, представленными в машинных кодах
Количество логических операций может быть вычисленно по формуле ![]() , где n – число переменных. Из формулы видно, что для двух переменных a и b логических операций 16. Основные из них: логическое сложение, логическое умножение, логическое отрицание, сложение по модулю 2.
, где n – число переменных. Из формулы видно, что для двух переменных a и b логических операций 16. Основные из них: логическое сложение, логическое умножение, логическое отрицание, сложение по модулю 2.
| Для выполнения логических операций, используют таблицы истинности:Логическое сложение a Ú b | Логическое умножение a & b | Логическое отрицание | Сложение по модулю 2 a Å b | ||||||||||
| a \ b | 1 | 0 | a \ b | 1 | 0 | a |
| a \ b | 1 | 0 | |||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | |||
Задание:
а) произвести логическое сложение чисел А и С:
| Ú | 0|000000100110011 |
| 0|000000001011011 | |
| 0|000000101111011 |
б) произвести логическое умножение чисел А и С:
| & | 0|000000100110011 |
| 0|000000001011011 | |
| 0|000000000010011 |
в) произвести сложение чисел А и С по модулю 2.
| Å | 0|000000100110011 |
| 0|000000001011011 | |
| 0|000000101101000 |
г) произвести логический сдвиг: влево для чисел А и –А, вправо для С и –С
| A | –A | ||
| 0|000000100110011 | 1|111111011001101 | Число | |
| 0|000001001100110 | 1|111110110011010 | Результат сдвига влево |
| C | –C | ||
| 0|000000001011011 | 1|111111110100101 | Число | |
| 0|000000000101101 | 0|111111111010010 | Результат сдвига вправо |
д) произвести логический циклический сдвиг: влево для чисел А и –А, вправо для чисел С и –С
| A | –A | ||
| 0|000000100110011 | 1|111111011001101 | Число | |
| 0|000010011001100 | 1|111101100110100 | Результат сдвига влево на 2 бита |
| C | –C | ||
| 0|000000001011011 | 1|111111110100101 | Число | |
| 0|000000000010110 | 0|011111111101001 | Результат сдвига вправо на 2 бита |
e) произвести арифметический сдвиг: влево для чисел А и –А, вправо для чисел С и –С
| A | –A | ||
| 0|000000100110011 | 1|111111011001101 | Число | |
| 0|000001001100110 | 1|111110110011010 | Результат сдвига влево |
| C | –C | ||
| 0|000000001011011 | 1|111111110100101 | Число | |
| 0|000000000101101 | 1|011111111010010 | Результат сдвига вправо |
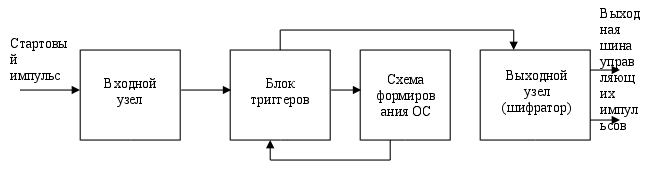
Глава 2. Методы контроля работы ЦА
Похожие работы
... в народном хозяйстве. Специальная часть. 3. 1. Определение задачи. Из задания на курсовое проектирование определим суть задачи: для некоторого синхронного цифрового автомата необходимо спроектировать устройство управления на основе жёсткой логики, которое в соответствии с заданными кодами микрокоманд формирует на выходной десятиразрядной шине управляющую последовательность цифровых сигналов. 3. ...
... . Функционирование цифрового автомата проверить на примере массива данных состоящей из шести элементов. Элементы массива A=5, B=2, x=2. Функционирование цифрового автомата представлено в табл.4 R1 R R3 R4 Sm1 Sm2 Выполняемая операция 0011 y1:R1ßx 0011 y2:R2ßB 0101 ...
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...
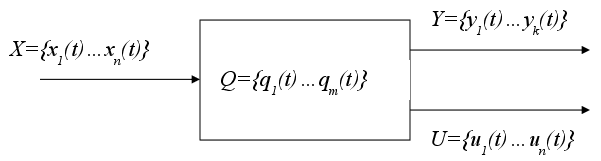
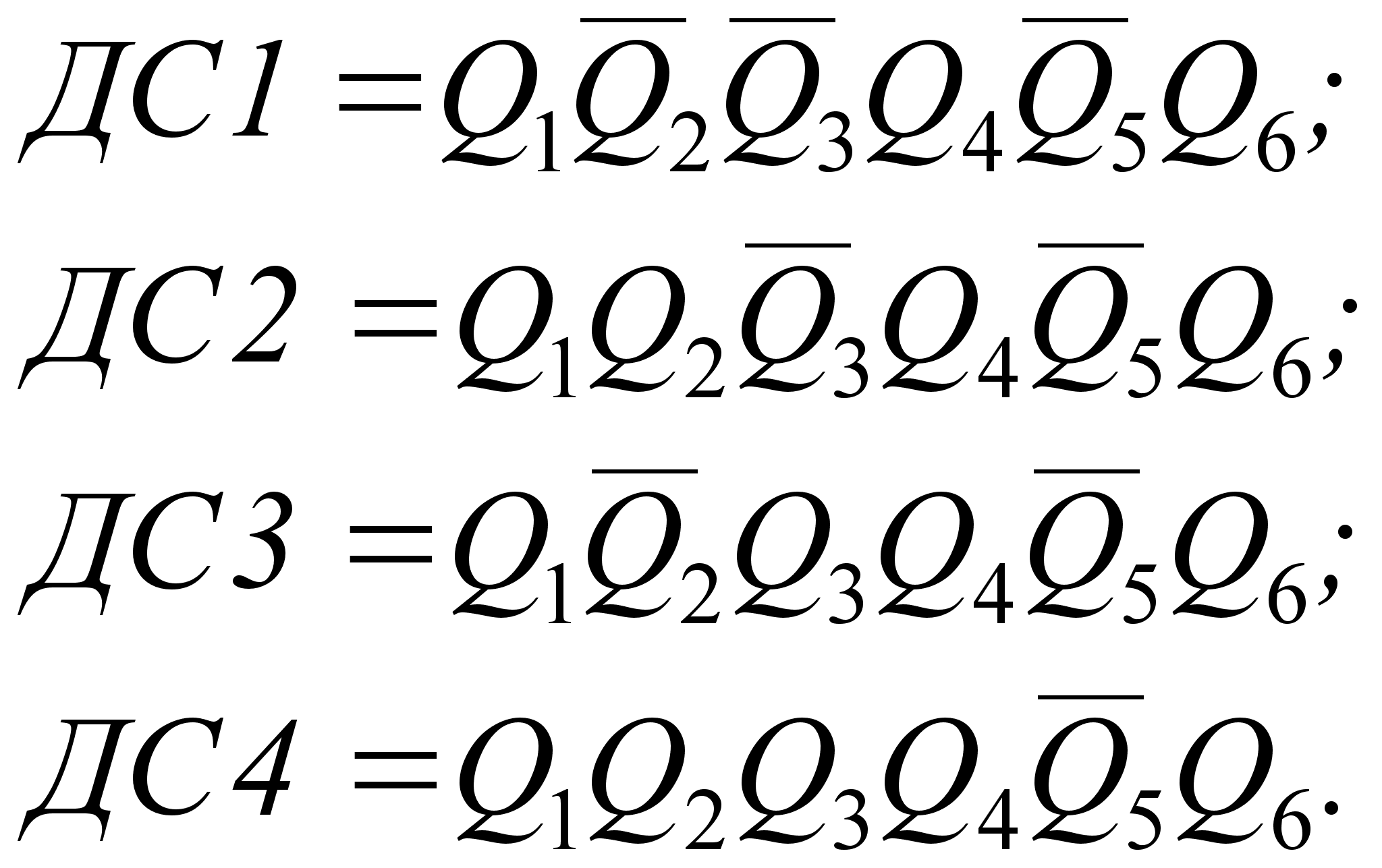
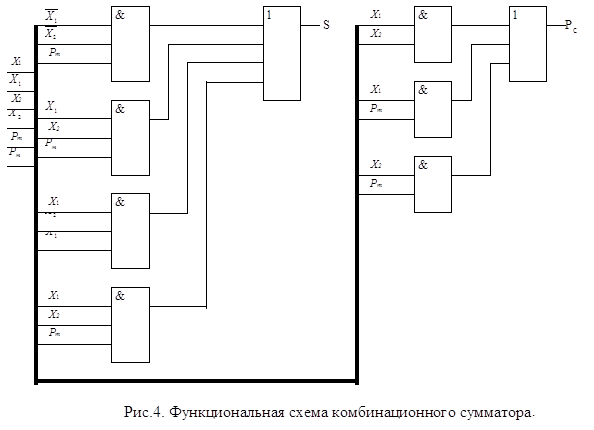
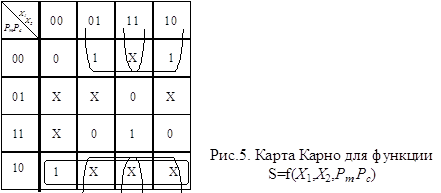
0 комментариев