Навигация
Корректирующая способность кодов
2.1 Корректирующая способность кодов
При работе ЦА могут произойти те или иные сбои, приводящие к искажению информации. Поэтому при проектировании ЦА должны предусматриваться средства, позволяющие контролировать, выявлять и исправлять возникающие ошибки. Решение всех задач контроля становится возможным только при наличии определенной избыточности информации, которая сопровождает основную информацию. Иначе говоря, при представлении числа в каком-либо коде, необходимо предусмотретьв этом коде дополнительные (контрольные) разряды.
Систематический код – это код, содержащий в себе информационные и контрольные разряды. В контрольные разряды записывается некоторая информация об исходном числе, поэтому систематический код обладает избыточностью.
При этом абсолютная избыточность будет выражаться количеством контрольных разрядов – k, а относительная избыточность – ![]() , где m – количество информационных разрядов.
, где m – количество информационных разрядов.
Понятие корректирующей способности кода связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Корректирующая способность кода связана понятием кодового расстояния.
Кодовое расстояние (Хемингово расстояние) d для кодовых комбинаций A и B определяется как вес такой третьей комбинации, которая получается сложением исходных комбинаций по модулю 2. Вес кодовой комбинации V – это количество единиц содержащихся в кодовой комбинации.
Например, A=100111001 и B=011011100. Отсюда веса кодовых комбинаций будут равны: V(A)=5, V(B)=5. Кодовая комбинация C=A+B=111100101, вес этой кодовой комбинации равен V(C)=6. Таким образом кодовое расстояние для A и B – d(A,B)=V(C)=6.
В любой позиционной системе счисления минимальное кодовое расстояние равно 1. В теории кодирования показано, что систематический код обладает способностью обнаружения ошибки только тогда, когда код расстояния для него больше или равен 2t. Следовательно, ![]() , где t – кратность обнаруживаемых ошибок. Это означает, что между соседними кодовыми комбинациями должна существовать, по крайней мере одна кодовая комбинация.
, где t – кратность обнаруживаемых ошибок. Это означает, что между соседними кодовыми комбинациями должна существовать, по крайней мере одна кодовая комбинация.
2.2 Метод четности / нечетности. Коды Хеминга
Если в математическом коде выделен один контрольный разряд, то к каждому двоичному числу добавляется один избыточный разряд. В этот разряд записывается 1 или 0 с таким условием, чтобы сумма цифр по модулю 2 была равна 0 для случая четности или 1 для случая нечетности. Появление ошибки в кодировании обнруживается по нарушению четности / нечетности. При таком кодировании допускается, что может возникнуть только одна ошибка.
Пример реализации метода четности:
Число | Контрольный разряд | Проверка |
| 10101011 | 1 | 0 |
| 11001010 | 0 | 0 |
| 10010001 | 1 | 0 |
| 11001011 | 0 | 1 – ошибка |
Можно представить и несколько видоизмененный способ контроля по методу четности / нечетности. Длинное слово разбивается на группы, каждая из которых содержит n разрядов. Контрольные разряды – k, выделяются всем группам по строкам и столбцам согласно следующей схеме:

Увеличение избыточности приводит к тому, что появляется возможность не только обнаружить ошибку, но и исправить ее.
Например: число 1000111011010101110010101 представим по указанной выше схеме, получим:
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
Теперь, если при передаче было получено число:
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
Тогда проверка показывает, что ошибка возникла в информации третьей строки и четвертого столбца. Следовательно, разряд, содержащий ошибочную информацию, находится на пересечении третьей строки и четвертого столбца. Ошибку можно устранить изменив 0 на 1.
Код Хэмминга – биочный систематический код, то есть состоящий из информационных и корректирующих символов, рассположенных по строго определенной системе, имеющих одинаковую длину и всегда занимающих строго определенные места в кодовых комбинациях.
При передаче кода может быть искажен или не искажен любой символ. Если длина кода – n символов, то ![]() – полное количество комбинаций кода. По методике Хэмминга можно определить число информационных символов кода, обнаруживающего и корректирующего одиночную ошибку следующим образом:
– полное количество комбинаций кода. По методике Хэмминга можно определить число информационных символов кода, обнаруживающего и корректирующего одиночную ошибку следующим образом:
![]()
![]()
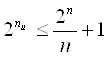 , где
, где
![]() – число информационных символов в коде;
– число информационных символов в коде;
![]() – число контрольных символов;
– число контрольных символов;
![]() – длина кода Хемминга.
– длина кода Хемминга.
Соотношение n, ![]() и
и ![]() для кода Хэмминга можно представить в виде таблицы:
для кода Хэмминга можно представить в виде таблицы:
Таблица 2.2.a
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|
| 0 | 0 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 11 |
|
| 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 5 |
Пусть необходимо передать число 1110=10112. Значит ![]() . Используя таблицу 2.2.a получаем:
. Используя таблицу 2.2.a получаем: ![]() ,
, ![]() .
.
Далее необходимо определить на какой позиции должны находиться контрольные коэффициенты. Позиция контрольных коэффициентов – k в коде вычисляется по формуле – ![]() , где i – порядковый номер коэффициента k. Получаем 7-разрядный код:
, где i – порядковый номер коэффициента k. Получаем 7-разрядный код:
Таблица 2.2.c
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | Разряды кода Хемминга |
| k1 | k2 | И4 | k3 | И3 | И2 | И1 | Назначение разрядов |
| 1 | 0 | 1 | 1 | Значение разряда |
Где ki – контрольный коэффициент (отсчет идет слева на право); Иi – информационный символ (отсчет идет справа на лево).
Значение контрольных коэффициентов по правилу: если сумма единиц на проверочных позициях четная, то значение контрольного коэффициента равно 0, в противном случае – 1.
Таблица 2.2.d
| Позиция контрольного коэффициента | Проверочные позиции |
| 1 | 1, 3, 5, 7, 9, 11, 13… |
| 2 | 2, 3, 6, 7, 10, 11, 14… |
| 4 | 4, 5, 6, 7, 12, 13, 14… |
| 8 | 8, 9, 10, 11, 12, 13, 14… |
Итак, используя таблицу 2.2.d назодим значения контрольных коэффициентов ki:
k1 = 1 + 0 + 1 = 0;
k2 = 1 + 1 + 1 = 1;
k3 = 0 + 1 +1 = 0.
Получим код Хемминга 0110011 для передачи числа 1110.
Теперь рассмотрим пример корректировки полученного кодированного в коде Хемминга числа, в котором есть сбой. Получили число 0110001. Для исправления ошибки необходимо определить позицию, в которой произошел сбой. Для этого определяем значения контрольных коэффициентов, используя таблицу 2.2.d:
k1 = 0 + 1 + 0 + 1 = 0 – нет ошибки;
k2 = 1 + 1 + 0+ 1 = 1 – ошибка;
k3 = 0 + 0 +0 + 1 = 1 – ошибка.
Номер ошибочного разряда совпадает с суммой позиций контрольных коэффициентов, указавших на наличие ошибки т.е. 2 + 4 = 6. Для исправления ошибки достаточно инвертировать значение 6-го разряда.
Задание. Построить код Хемминга для числа А.
A = 30710 = 1001100112
Используя таблицу 2.2.a получаем: ![]() ,
, ![]() .
.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | Разряды кода Хемминга |
| k1 | k2 | И9 | k3 | И8 | И7 | И6 | k4 | И5 | И4 | И3 | И2 | И1 | Назначение разрядов |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | Значение разряда |
k1 = 1 + 0 + 1 + 1 + 0 + 1 = 0;
k2 = 1 + 0 + 1 + 0 + 0 = 0;
k3 = 0 + 0 +1 + 1 + 1 = 1;
k4 = 1 + 0 + 0 + 1 + 1 = 1.
Получим код Хемминга 0011001110011.
При передаче, получили код с ошибкой 0011001110111. Проверяем:
k1 = 0 + 1 + 0 + 1 + 1 + 1 + 1 = 1; – ошибка;
k2 = 0 + 1 + 0 + 1 + 0 + 1 = 1; – ошибка;
k3 = 1 + 0 + 0 +1 + 1 + 1 = 0; – нет ошибки;
k4 = 1 + 1 + 0 + 1 + 1 + 1 = 1 – ошибка.
Ошибка находится в разряде 1 + 2 + 8 = 11, инвертируем 11-й разряд и получаем исходный код Хемминга.
Похожие работы
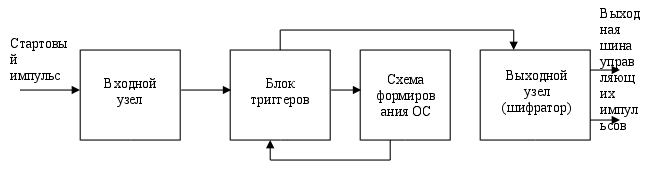
... в народном хозяйстве. Специальная часть. 3. 1. Определение задачи. Из задания на курсовое проектирование определим суть задачи: для некоторого синхронного цифрового автомата необходимо спроектировать устройство управления на основе жёсткой логики, которое в соответствии с заданными кодами микрокоманд формирует на выходной десятиразрядной шине управляющую последовательность цифровых сигналов. 3. ...
... . Функционирование цифрового автомата проверить на примере массива данных состоящей из шести элементов. Элементы массива A=5, B=2, x=2. Функционирование цифрового автомата представлено в табл.4 R1 R R3 R4 Sm1 Sm2 Выполняемая операция 0011 y1:R1ßx 0011 y2:R2ßB 0101 ...
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...
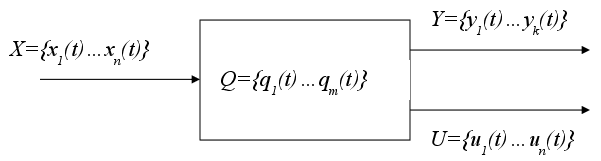
0 комментариев