Навигация
Синтез зубчатого механизма
3. Синтез зубчатого механизма.
Дано:
Схема механизма.
Угловая скорость входного звена ωд=125 с-1.
Угловая скорость выходного звена ωвм=15 с-1.
Модуль зубчатых колёс m=4мм.
Z5=13.
Z6=20.
На схеме представлен комбинированный зубчатый механизм, который состоит из:
- планетарного механизма (1, 2, 3, 4 и водила Н, колесо 4 остановлено);
- одноступенчатого зубчатого механизма с неподвижными осями (колёса 5 и 6).
3.1 Определение геометрических параметров зубчатой передачи.
Передаточное отношение многоступенчатого механизма равно произведению передаточных отношений его ступеней:
![]()
Для планетарного механизма:
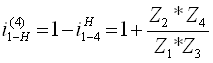
Для одноступенчатой зубчатой передачи:
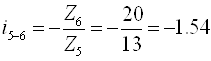
Передаточное отношение всего механизма:
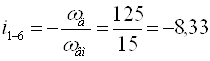
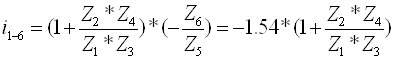
Тогда ![]()
![]() = 4
= 4
Запишем условие соосности:
Z1+Z2=Z4-Z3
Из него ясно, что Z4 должно быть больше Z3. Соотношение ![]() заменяем отношением сомножителей a, b, c, d, каждый из которых соответственно пропорционален числу зубьев.
заменяем отношением сомножителей a, b, c, d, каждый из которых соответственно пропорционален числу зубьев.
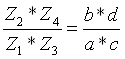 , следовательно, a + b = d - с.
, следовательно, a + b = d - с.
Чтобы условие соосности выполнялось в любом случае, умножим правую часть равенства на левую, а левую - на правую:
(a + b) * (d - с) = (d - с) * (a + b).
Так как сомножители a, b, c, d пропорциональны числам зубьев, то для определения последних требуется умножить каждый сомножителей на коэффициент пропорциональности γ. Очевидно, что γ - любое положительное число. Таким образом, получим:
γ * (a + b) * (d - с) = γ * (d - с) * (a + b).
Преобразуем равенство к виду:
γ * a * (d - с) + γ * b * (d - с) = γ * d * (a + b) - γ * с * (a + b).
Теперь можно принять, что:
Z1 = γ * a * (d - с), Z2 = γ * b * (d - с),
Z3 = γ * с * (a + b), Z4 = γ * d * (a + b).
Разобьём передаточное отношение ![]() на четыре сомножителя, которые должны быть целыми числами. Это можно выполнить различным образом:
на четыре сомножителя, которые должны быть целыми числами. Это можно выполнить различным образом:
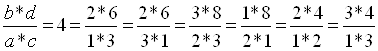
Рассмотрим третий вариант: а = 2, b = 3, с = 3, d = 8. Решение ищем в ранее полученном виде:
Z1 = γ * a * (d - с) = 2 * (8 - 3) * γ = 2 * γ,
Z2 = γ * b * (d - с) = 3 * (8 - 3) * γ = 3 * γ,
Z3 = γ * с * (a + b) = 3 * (2 + 3) * γ = 3 * γ,
Z4 = γ * d * (a + b) = 8 * (2 + 3) * γ = 8 * γ.
Наименьшим должно быть зубчатое колесо Z1. Число зубьев колеса Z1 определяется из условия отсутствия интерференции зубьев при зацеплении с колесом Z2; Z1 должно быть более 17, так как при 17 зубьях правильное зацепление возможно лишь с зубчатой рейкой. Примем γ = 9, тогда:
Z1 = 18, Z2 = 27, Z3 = 27, Z4 = 72.
Условия правильного зацепления выполняется (согласно таблице):
Z1 > 17, а Z4 > Z3 + 8.
Определим возможное число сателлитов по внешнему зацеплению:
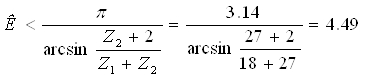
По внутреннему зацеплению:
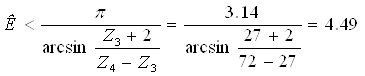
Число сателлитов может быть не более трёх. Проверим условие сборки при трёх сателлитах:
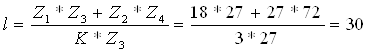
Условие сборки выполняется, так как l = 30 - целое число.
Определяем диаметры делительных окружностей зубчатых колёс:
d1 = Z1 * m = 18 * 4 = 72 мм,
d2 = Z2 * m = 27 * 4 = 108 мм,
d3 = Z3 * m = 27 * 4 = 108 мм,
d4 = Z4 * m = 72 * 4 = 288 мм,
d5 = Z5 * m = 13 * 4 = 52 мм,
d6 = Z6 * m = 20 * 4 = 80 мм.
Похожие работы
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
... Найденные при силовом анализе механизма величины представлены в таблице 1.4. 57 48 65 0.22 0.6 0.8 0.79 0.7 0.9 73 1.9 Таблица 1.4. Силовой анализ механизма 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое ...
... длину вектора и переведем ее обратно: = 79 мм = 2370 Н 2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции , моменты инерции и реакции в кинематических парах R. Под ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...

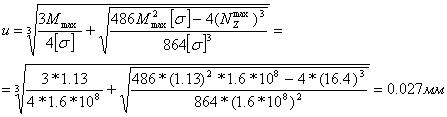
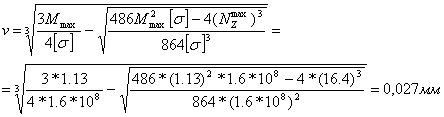
0 комментариев