Навигация
Построение плана линейных скоростей
3.2 Построение плана линейных скоростей.
Построение плана возможно, если у каждого звена будут известны скорости минимум двух его точек. Известными являются скорости точек звеньев, движения которых задано, а так же скорости точек неподвижных геометрических осей вращения звеньев (они равны нулю).
При построении плана используем свойство эвольвентного зацепления: скорость полюса зацепления является общей для точек начальных окружностей зацепляющих колёс.
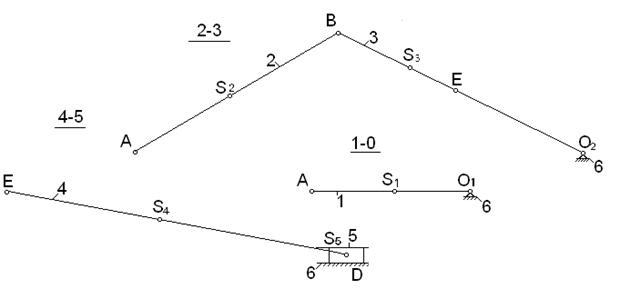
На чертеже строим схему механизма, учитывая масштабный коэффициент:
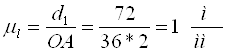
Определяем скорость точки А:
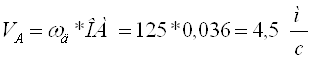
На плане линейных скоростей проводим ось Y-Y. От неё из точки А1 строим вектор-отрезок скорости т.А (А1а = 45 мм). Тогда масштабный коэффициент:
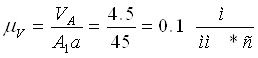
Теперь можно определить скорости всех точек звена 1, так как известны скорости двух его точек А и О ( скорость т.О равна нулю). Прямая, проходящая через точки а и О1, и будет изображать скорости всех точек звена 1.
Известно, что колёса Z2 и Z3 равны и их центры располагаются на одной оси (жёстко связаны). Следовательно скорости всех их точек будут располагаться на одной прямой, проходящей через точки В1 (полюс зацепления колёс Z3 и Z4, при чём колесо Z4 остановлено) и а (так как т.А - полюс зацепления колёс Z1 и Z2). Для того, чтобы определить скорость т.С, необходимо провести из т.С1 горизонтальную прямую до пересечения с прямой В1а. Отрезок С1с будет вектором скорости т.С:
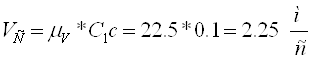
Сателлит проходит через две точки: О' (её скорость равна нулю, так как она располагается на одной прямой с т.О) и С (её скорость известна), следовательно, скорости всех точек сателлита будут лежать на прямой, проходящей через точки О1 и с.
Скорость точки Е - отрезок построенный из точки Е1 до пересечения с прямой О1с:
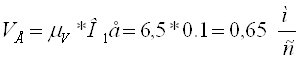
Скорость т.D равна нулю, скорость т.Е (полюс зацепления Z5 и Z6) известна, значит скорость всех точек 6 звена есть прямая D1е.
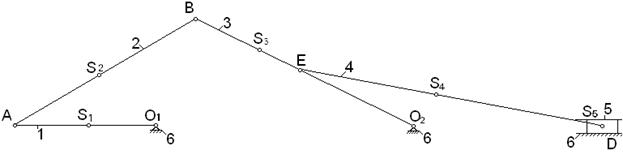
3.3 Построение плана угловых скоростей.
Проводим горизонтальную прямую и перпендикулярно к ней строим отрезок Н произвольной величины (50 мм). Затем из конца отрезка (т.О) проводим лучи параллельные линиям распределения скоростей звеньев. на горизонтальной прямой отсекутся отрезки ωi, изображающие в масштабе ![]() угловые скорости звеньев механизма.
угловые скорости звеньев механизма.
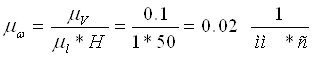
По отношению отрезков может быть определено передаточное отношение между звеньями механизма.
Передаточное отношение от звена 5 к звену 6:
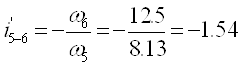
Погрешность определения передаточного отношения графическим методом относительно аналитического метода:
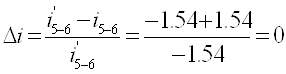
4. Синтез кулачкового механизма.
Дано:
Диаграмма аналоговых ускорений.
Схема кулачкового механизма.
φб.о.= 400.
φд.о.= 600.
αдоп= 250.
Smax=40 мм.
Рассчитаем недостающие фазовые углы:
φраб.= φд.о+ φу
φх.х.= φб.о+ φв
φу= φв
φ= φраб.+ φх.х.= φу + φв+600+400 =3600
φу = φв=1300
4.1 Построение графиков аналогов ускорений.
Строится он в произвольном масштабе (максимальная ордината должна быть не менее 80 мм) с учётом фазовых углов удаленияφу, дальней остановки φд.о, возвращения φв, ближней остановки φб.о. При этом следует соблюдать условия равенства площадей F1=F2, F3=F4, так как площади F1 и F2, F3 и F4 в определённом масштабе представляют собой максимальное значение ординаты графика аналога скоростей соответственно на фазе удаления и фазе возвращения. Если φу= φв, то F1=F2=F3=F4.
Задаём оси координат аφ и φ. Затем строим график аналоговых ускорений с максимальной ординатой в 50мм, учитывая масштабные коэффициенты:
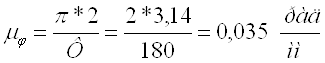
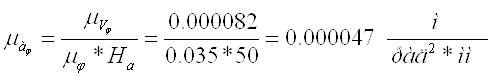
4.2 Построение графиков аналогов скоростей.
График аналогов скоростей строится графическим интегрированием графика аналогов ускорений. При интегрировании полюсное расстояние Н следует брать таким, чтобы максимальная ордината графика была не менее 80 мм. А также необходимо учитывать масштабный коэффициент:
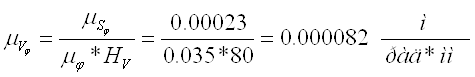
4.3 Построение графиков аналогов перемещений
График аналогов перемещений строится графическим интегрированием графика аналогов скоростей. При интегрировании полюсное расстояние Н следует брать таким, чтобы максимальная ордината графика была не менее 80 мм. А также необходимо учитывать масштабный коэффициент:
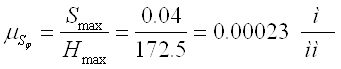
4.4 Определение начального радиуса кулачка.
Параллельно траектории движения толкателя кулачкового механизма проводится прямая линия.
От произвольной точки на этой линии (нулевая точка) по направлению перемещения толкателя на фазе удаления откладываются отрезки 0-1, 0-2, 0-3, ..., 0-6, соответствующие отрезкам 1-1, 2-2, 3-3, ..., 6-6 фазы удаления графика перемещений. На фазе возвращения (тоже от нулевой точки) откладываются отрезки 0-10, 0-11, 0-12, ..., 0-16, соответствующие отрезкам 10-10, 11-11, 12-12, ..., 16-16 фазы возвращения графика перемещений, учитывая масштабный коэффициент:
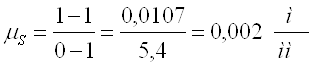
Из точек 1, 2, 3, ... перпендикулярно траектории движения толкателя в сторону векторов его скоростей на фазах удаления и возвращения), повёрнутых на 900 в направлении угловой скорости кулачка ω1 откладываются соответствующие отрезки аналогов скоростей (из графика аналогов скоростей). Масштаб этих отрезков должен быть тем же, что и масштаб отрезков перемещения толкателя, отложенных на траектории его движения. Для этого соответствующую ординату с графика аналогов скоростей необходимо умножить на масштабный коэффициент ![]() изображения аналогов скоростей. Получим истинную величину аналога скорости. Чтобы изобразить аналог скорости в масштабе перемещений, необходимо истинную величину аналога скорости разделить на масштабный коэффициент
изображения аналогов скоростей. Получим истинную величину аналога скорости. Чтобы изобразить аналог скорости в масштабе перемещений, необходимо истинную величину аналога скорости разделить на масштабный коэффициент ![]() перемещений:
перемещений:
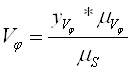
Концы отрезков соединяют плавной кривой.
Касательно к полученной кривой под максимально допустимым углом давления αдоп к траектории движения толкателя проводятся лучи, таким образом, чтобы точка их пересечения О1 и нулевая точка О располагались по одну сторону от кривой. Расстояние между точкой, принимаемой за ось вращения кулачка и точкой О и будет представлять собой величину начального радиуса кулачка.
Если за ось вращения кулачка принять точку пересечения лучей О1, получим минимально возможный начальный радиус кулачка.
4.5 Построение профиля кулачка.
При построении профиля кулачка все линейные величины откладываются в одном масштабе.
Проводим окружность с центром О1, радиус которой равен начальному радиусу кулачка.
Обозначаем направление вращения кулачка ω.
Построенная окружность делится на столько равных частей, сколько их имеет ось абсцисс графика перемещений. Нумерация точек производится в направлении, обратном направлению вращения кулачка.
Через полученные точки касательно к окружности с центром в точке О1 проводятся траектории движения толкателя в обращённом движении.
От точек 0,1, 2, ..., 17 пересечения траектории с окружностью начального радиуса откладываются отрезки 1-1’, 2-2’, 3-3’, ..., 17-17’, соответствующие отрезкам 1-1, 2-2, 3-3, ..., 17-17 графика перемещений.
Полученные точки соединяются плавной кривой, которая и будет представлять собой центровой профиль кулачка.
Согласно графику аналогов перемещений отмечаются фазовые углы.
Список литературы.
1. Методические указания к курсовому проектированию по теории механизмов и машин. «Кинематический анализ плоских рычажных механизмов Горький 1995.
2. Методические указания к курсовому проектированию по курсу теория механизмов и машин. «Кинетостатический (силовой) анализ плоского рычажного механизма». Горький 1995.
3. Методические указания к курсовому проектированию по курсу теория механизмов и машин. «Синтез кулачковых механизмов».. Горький 1995.
4. Методические указания к курсовому проектированию по теории механизмов и машин. «Синтез зубчатой передачи». Горький 1995.
Похожие работы
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
... Найденные при силовом анализе механизма величины представлены в таблице 1.4. 57 48 65 0.22 0.6 0.8 0.79 0.7 0.9 73 1.9 Таблица 1.4. Силовой анализ механизма 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое ...
... длину вектора и переведем ее обратно: = 79 мм = 2370 Н 2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции , моменты инерции и реакции в кинематических парах R. Под ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
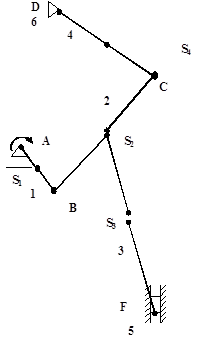

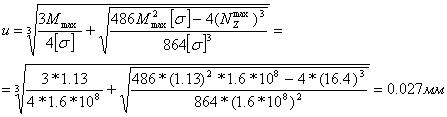
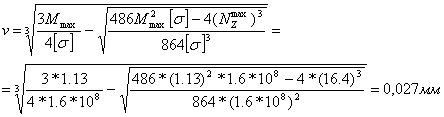
0 комментариев