Навигация
3.2.3 Проверочный расчет валов
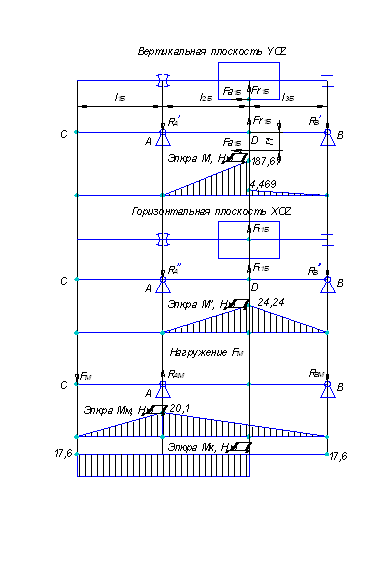
Плоскость YOZ (вертикальная).
Для определения реакции Rb воспользуемся уравнением (3.4)
- Fr1 ּ 28+Fa2 ּ 45+Fr2 ּ 39+Fa1 ּ 13+Rb ּ 82 = 0;
Подставляя радиальные усилия Fr1 = 0,22 кН, Fr2 = 0,068 кН, Fa1=0.09, Fa2=0.4 получим Rb = 0.007 кН.
Для определения реакции RА воспользуемся уравнением (3.5)
Fa1 ּ 13-Fr1 ּ 110-Fr2 ּ 43+ Fa2 ּ45 +RA ּ 82 = 0;
RA = 0,295 кН.
Строим эпюру изгибающих моментов Мх (z).
Сечение 1-1: Мх определяется по формуле (3.7).
-Fr2 ּ z+Fa ּ13
Точка А: z =0, Мх = 1,17.
Точка С: z =28 мм, Мх = 4,99 Нм.
Сечение 2-2: Мх =-Fr2 ּ z + Fa ּ13+Ra ּ( z -28), (3.18)
Точка В: z =0, Мх = -2.065.
Точка Д: z = 67мм, Мх = -2.065 Нм.
Сечение 3-3 Mx= Rby ּz
Точка А: z =0, Мх = 0.
Точка С: z =43 мм, Мх = 0.301 Нм.
Плоскость XOZ (горизонтальная).
Определяем реакции в опорах .
Реакцию Rb определяем по формуле (3.4)
- Fr1 ּ 28 – Ft2 ּ 39 -Rb ּ 82 = 0;
Подставляя окружные усилия Ft2 = 0,204 кН и Ft1 = 0.66 кН получим Rb = 0.128кН.
Реакцию RА определяем по формуле (3.5)
Ft1 ּ 110 + Ft2 ּ 43 - RАx ּ 82 = 0;
RАx = 0.992 кН.
Строим эпюру изгибающих моментов МY (z).
Сечение 1-1: МY определяется по формуле (3.7)
Точка А: z =0, МY = 0.
Точка С: z = 28мм, МY 18,48 Нм.
Сечение 2-2:
МY = Ft1 ּz-Ra ּ(z-36)
Точка B: z = 28, МY =18.48, z = 28, MY = 275.9
Сечение 3-3 MY = Rb ּz; z = 0, МY =0; z = 43, MY = 81.5
Опасным являются сечения в т.А (рис.3.2)
Проверяем сечение А.
Находим напряжение изгиба по формуле (3.12)
σ = 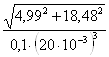 = 23.9 МПа.,
= 23.9 МПа.,
Находим напряжение кручения по формуле (3.13)
τ = ![]() = 5.6 МПа.
= 5.6 МПа.
Полученные напряжения подставляем в выражение (3.11)
σэ = 25.8 МПа.
Предел выносливости для Ст.45 σ-1 = 410 МПа [2].
Коэффициент запаса сопротивления усталости назначаем S=2
Напрессованные на вал детали создают концентрацию напряжений. Влияние на сопротивление усталости напрессовки деталей существенно зависит от размеров. Поэтому ее влияние и влияние размера учитывают общим коэффициентом![]()
![]() (3.18)
(3.18)
где ζ’-коэффициент , учитывающий предел прочности материала вала;
ζ’’- коэффициент , учитывающий давление в посадке.
ζ’=0,305+0,0014ּσв (3.19)
ζ’’=0,65+0,014ּp (3.20)
ζ’’=1(при p>25МПа) наихудший вариант
ζ’=0,305+0,0014ּ900=1,565
![]() =2,9[1]
=2,9[1]
![]()
Проверяем условие (3.10)
25,8≤![]()
25,8<45,6МПа
Условие выполняется, поэтому уточненный расчет производить нет необходимости.
3.3 Расчет промежуточного вала
3.3.1 Материалы и термообработка валов
Для изготовления промежуточного вала назначаем Ст. 45, улучшение. [σв]=900МПа, [στ]=380МПа
3.3.2 Проектный расчет валов
Подставляя крутящий момент Тпр = 153,1 Нм в выражение (3.14) получим
dк ≥(6-7) ![]() = 16,7-19,4 мм.
= 16,7-19,4 мм.
Назначаем dк = 18 мм. dбк ≥ 18+3 ּ 1 = 21 мм.
Назначаем dбк = 22 мм. dп = 18-3 ּ 1,5 = 13,5мм.
Назначаем dп = 17 мм. dбп ≥ 17+3 ּ1,5 = 20,5мм.
Назначаем dбп = 20 мм.
3.3.3 Проверочный расчет валов
Плоскость YOZ (вертикальная).
Для определения реакции Rb воспользуемся уравнением (3.4)
-Fa2 ּ de2/2+Ft2 ּ 40-Fr1 ּ 77-Rb ּ 127= 0;
Rb =.![]() =
=
Подставляя радиальные усилия Fr1 = 0.49 кН, Ft2 = 0.66, Fa2=0.22кН получим Rb = -0,118кН.
Для определения реакции RА воспользуемся уравнением (3.5)
- Fa2 ּ de2/2- Fr2 ּ87-Fr1 ּ 50 +RA ּ 127 = 0;
RA =![]() = 0,428кН.
= 0,428кН.
Строим эпюру изгибающих моментов Мх (z).
Сечение 1-1: Мх определяется по формуле (3.7).
Точка А: z =0, Мх = 0.
Точка С: z =40 мм, Мх = 17,12 Нм.
Сечение 2-2: Мх =Rа ּ z –Fr2(z-40),
Точка В: z =0, Мх = 17,12.
Точка Д: z = 37мм, Мх = 3,356 Нм.
Сечение 3-3: Мх = -RБ ּ z,
Точка В: z =0, Мх = 17,12.
Точка Д: z = 50мм, Мх = -5,9 Нм
Плоскость XOZ (горизонтальная).
Определяем реакции в опорах .
Реакцию Rb определяем по формуле (3.4)
Ft2 ּ 40 +Ft1 ּ 77 + Rb ּ 127 = 0;
Подставляя окружные усилия Ft2 = 0,66 кН и Ft1 = 1,35 кН получим Rb = -1,02 кН.
Реакцию RА определяем по формуле (3.5)
Ft1 ּ 50 + Ft2 ּ 87+ RА ּ 127 = 0; RА =0,99кН.
Строим эпюру изгибающих моментов МY (z).
Сечение 1-1: МY определяется по формуле (3.7)
Точка А: z =0, МY = 0.
Точка С: z = 40мм, МY = -39,6 Нм.
Сечение 2-2: МY = -Rа ּ40+Ft2(z-40)
Точка B: z = 40, МY =-39.6
Точка С: z = 37 мм, МY =-52,0Нм.
Сечение 3-3: МY = -Rb ּ z
Точка D: z = 40, МY =0
Точка С: z = 50 мм, МY =-52,0Нм
Опасным являются сечения С и Д (рис.3.2)
Проверяем сечение С.
Находим напряжение изгиба по формуле (3.12)
σ = 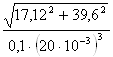 = 53.92 МПа.,
= 53.92 МПа.,
Находим напряжение кручения по формуле (3.13)
τ = ![]() = 13,35 МПа.
= 13,35 МПа.
Полученные напряжения подставляем в выражение (3.11)
σэ = ![]() = 78,39 МПа.
= 78,39 МПа.
σэ = ![]() = 58,67 МПа.
= 58,67 МПа.
Предел выносливости для стали 40Х σ-1 = 387 МПа [2].
Коэффициент запаса сопротивления усталости назначаем S=2
Напрессованные на вал детали создают концентрацию напряжений. Влияние на сопротивление усталости напрессовки деталей существенно зависит от размеров. Поэтому ее влияние и влияние размера учитывают общим коэффициентом![]() ζ’’=1(при p>25МПа) наихудший вариант
ζ’’=1(при p>25МПа) наихудший вариант
Полученные напряжения подставляем в выражение (3.19)
ζ’=0,305+0,0014ּ900=1,565
![]() =3,13[1]
=3,13[1]
Полученные значения подставляем в выражение (3.18)
![]()
Проверяем условие (3.10)
58,08≤![]()
58,08<61,82
Проверяем сечение Д.
Находим напряжение изгиба по формуле (3.12)
σ = 38,12 МПа.,
Находим напряжение кручения по формуле (3.13)
τ = ![]() = 5,43 МПа.
= 5,43 МПа.
Полученные напряжения подставляем в выражение (3.11)
σэ = ![]() = 39,26 МПа
= 39,26 МПа
Предел выносливости для стали 40Х σ-1 = 387 МПа [2].
Коэффициент влияния абсолютных размеров поперечного сечения ε= 0,72 [1].
Коэффициент запаса сопротивления усталости назначаем S = 2.
Коэффициент концентрации напряжения Кσ = 1,72 [1].
Kv=2, [1] для закалки ТВЧ
Проверяем условие (3.10)
39,26≤![]()
39,26≤88,87МПа
Условие выполняется, поэтому уточненный расчет производить нет необходимости.
3.4 Расчет тихоходного вала
3.4.1 Материалы и термообработка валов
Для изготовления тихоходного вала назначаем Ст. 45, улучшение.
[σв]=580МПа, [στ]=320МПа.
3.4.2 Проектный расчет валов
Диаметры различных участков вала определяют по формулам:
d ≥(5-6)![]() (3.21)
(3.21)
dn ≥d+2ּt (3.22)
dбп ≥ dn +3ּr (3.23)
dк ≥ dбп (3.24)
где Tmux - крутящий момент на тихоходном вале, Нм;
d, dn, dбп, dк, – диаметры отдельных участков вала, мм.
Подставляя крутящий момент Tmux = 671 Нм в выражение (3.21) получим
d ≥ (5-6) ![]() = 27.47-32.95 мм.
= 27.47-32.95 мм.
Согласуем полученный диапазон размеров с муфтой, выбранной по моменту на тихоходном валу
Назначаем d = 50 мм. dn ≥ 50+2ּ4= 58 мм.
Назначаем dn = 50 мм. dбп ≥ 50 +3ּ3 = 59 мм.
Назначаем dбп = 55 мм. Назначаем dк = 55 мм.
Похожие работы
... – проектный (приближенный) расчет валов на чистое кручение , 2-й — проверочный (уточненный) расчет валов на прочность по напряжениям изгиба и кручения. 1. Определение сил в зацеплении закрытых передач. В проектируемых приводах конструируются червячные редукторы с углом профиля в осевом сечении червяка 2а = 40° .Угол зацепления принят α= 20°. а) на колесе: 1.1 Окружная сила Ft2, Н: Ft2= где T2 ...
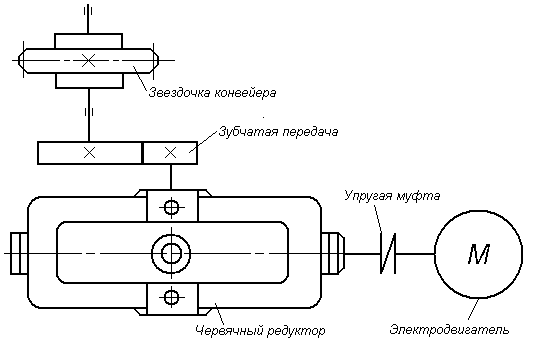
... валиками (индекс М), шаг : д)конструктивные особенности: на валу установлена одна звёздочка для тяговой пластинчатой цепи; приводной вал конвейера соединён с выходным валом редуктора посредством горизонтально расположенной цепной передачи; е) расчётный срок службы; ж) кратковременная перегрузка ; з) номер типового режима нагружения - 2. 10.1 Предварительная разработка конструкции ...
... – КПД зубчатой цилиндрической прямозубой передачи; η3 = 0,99 – КПД пары подшипников качения, η4 = 0,8 – КПД цепной передачи Потребная мощность электродвигателя Частота вращения вала двигателя nЭ = n3 ∙ uРЕД ∙ uЦИЛ Где: – частота вращения вала конвейера; uРЕД = 16…50 – интервал передаточных чисел редуктора; uЦИЛ = 2,5…5 – интервал передаточных ...
... проекта по “Деталям машин” были закреплены знания, полученные за прошедший период обучения в таких дисциплинах как: теоретическая механика, сопротивление материалов, материаловедение. Целью данного проекта является проектирование привода цепного конвейера, который состоит как из простых стандартных деталей, так и из деталей, форма и размеры которых определяются на основе конструкторских, те


0 комментариев