< 177

150 < 177

4.8 Проверочный расчет червячной передачи на изгибную прочность

Данный расчет позволяет проверить правильность размеров рассчитанной передачи с точки зрения ее нормальной работы по изгибным напряжениям, которые не должны превышать допустимых значения.

Расчетное напряжение изгиба рассчитывается по формуле

≤[σ]_F,(5.22)

где m — модуль, м;

Y_F – коэффициент формы зуба, определяемый с учетом эквивалентного числа зубьев.

Y_F = 1,71,

=20,8 МПа.

Из расчета следует, что 20,8≤38,5.

4.9 Тепловой расчет

Червячный редуктор в связи с низким значением К.П.Д. и вследствие этого высоким выделением тепла обязательно проверяют на нагрев.

Тепловой расчет передачи представлен в таблице 5.9.

Таблица 5.9

Наименование параметров	Обозначение	Расчетные формулы
Приведенный угол трения, °	φ′	φ′=1,2°
К.п.д. червячной передачи	η	η ==0,868
Мощность на червяке, кВт	Р	Р=2,2 кВт
Количество тепла, выделяемое в передаче, ккал/ч	Q	Q=860(1- η)Р=250
Коэффициент теплоотдачи, ккал/м2ч°	КТ	КТ=11
Температура масла в редукторе, °С	t1	t1=70°
Температура окружающей среды, °С	t0	t0=20°
Поверхность охлаждения, м2	S	S=0,196
Количество отдаваемого тепла, ккал/ч	Q1	Q1= КТ(t1- t0) S=107,8
Условие достаточности естественного охлаждения	-	Q≤Q1; 250≥107,8

Как видно из расчета таблицы 5.9, требуется искусственное охлаждение редуктора.

5 . СМАЗКА

Условия эффективной смазки червячных передач: достаточное покрытие рабочих поверхностей зубьев и подшипников масляным слоем, отвод такого количества тепла, которое требуется для предотвращения чрезмерного нагрева, малое сопротивление смазочной среды.

Смазка передачи осуществляется окунанием. Способ – картерный непроточный. Сорт масла – Автотракторное АК-15 ГОСТ 1862-63.

6 КОНСТРУИРОВАНИЕ ВАЛОВ РЕДУКТОРА 6.1 Исходные данные для расчета

Вращающий момент на быстроходном валу редуктора Т₁ = 14,0 Н×м, на тихоходном валу Т₂ = 550 Н×м. силы в червячном зацеплении редуктора:

F_t1 = F_a2 = 700 Н;

F_t2 = F_a1 = 4075 Н;

F_r1 = F_r2 = 1500 Н;

Размеры червяка d₁ = 50 мм, d_f1 = 34 мм. Размеры червячного колеса d₂ = 270 мм.

При расчете валов редуктора необходимо учитывать консольную нагрузку и считать ее приложенной в середине посадочной консольной части вала.

На быстроходном валу радиальную консольную нагрузку определяем по формуле.

F_к1 =80,(7.1)

F_к1 =80= 300 Н.

На тихоходном валу радиальную нагрузку определяем по формуле (7.2):

F_к2 =125,(7.2)

F_к2 = 125= 2930 Н.

В соответствии с конструкцией редуктора заданного типа из эскизной компоновки и ориентировочного расчета валов получим необходимые расстояния до опор валов и приложенных нагрузок.

6.2 Приближенный расчет быстроходного вала

Материал вала – сталь 40ХН, для которой предел выносливости после улучшения:

σ_-1 = 0,35σ_b + (70…120),(7.3)

где σ_b = 920 МПа,

σ_-1 = 0,35×920 + 100 = 422 МПа.

Допускается напряжение изгиба при симметричном цикле напряжений:

[σ_n]_-1 = ,(7.4)

где [n] = 1,7 - – допускаемый коэффициент запаса прочности для опасного сечения;

K_σ = 2,0 – допускаемый коэффициент концентрации напряжений;

K_pn = 1 – коэффициент режима нагрузки при расчете на изгиб.

[σ_n]_-1 =  = 124 МПа.

6.2.1 Составить расчетную схему (рисунок 7.1) быстроходного вала в соответствии со схемой действия сил и эскизной компоновкой.

Строим эпюры изгибающих моментов.

В вертикальной плоскости YOZ рисунок 7.1.

а) определим опорные реакции от действия сил F_t1:

R_ay = R_cy= = 350 Н.

б) проверим правильность определения реакций:

ΣY = - R_ay + F_t1 - R_cy = -350 + 700 – 350 = 0

Реакции определены верно.

в) строим эпюру изгибающих моментов, для этого определим их значения в характерных сечениях вала:

-   в сечении А М = 0;

-   в сечении B М = R_ay ×125×10^-3 = 350×95×10^-3 = 43,8 Н×м;

-   в сечении С М = 0.

Следовательно, максимальный изгибающий момент будет в сечении В. Откладываем его на сжатом волокне вала (рис. 7.1.г.).

В горизонтальной плоскости XOZ (рис. 7.1.д)

а) определим опорные реакции от действия сил F_r1, F_a1, F_к1 из условия статики как сумма моментов относительно левой А и правой С опор.

ΣМ_А = 0 - F_r1×125 – F_a1× + R_cx×250 + F_k1×335 = 0

R_cx =  = 755,5 Н.

ΣМ_С = 0 R_АХ ×250 – F_r1×125 + F_a1×25 - F_k1×85 = 0

R_АХ =  = 444,5 Н.

б) проверим правильность определения реакций

ΣХ = R_АХ - F_r1 + R_cx - F_k1 =444,5 – 1500 + 755,5 + 300 = 0,

то есть реакции определены верно.

в) строим эпюру изгибающих моментов определяя их значение в характерных сечениях вала:

-   в сечении А М = 0;

-   в сечении В действуют изгибающие моменты от реакций R_AX и F_a1, М= R_AX×125×10^-3 = 444,5×125×10^-3 = 55,6 Н×м; М= F_a1×25×10^-3 = 4075×25×10^-3 = 101,9 Н×м.

-   в сечении С М= F_k1×85×10^-3 = 300×85×10^-3 = 25,5 Н×м;

-   в сечении D М = 0.

В сечении В направления изгибающих моментов совпадают по направлению. Откладываем значение М вверх от оси, а затем из этой же точки откладываем Мвверх, т.е.

М= М + М= 55,6 +101,9 = 157,5 Н×м;

г) проверим правильность определения момента в сечении В от сил
F_k1 и R_cx:

М= R_cx×125×10^-3 + F_k1×210×10^-3 = 755,5×125×10^-3 + 300×210×10^-3 = 157,5 Н×м.

д) строим эпюру крутящих моментов (рис. 8.1.ж).

Передача его происходит вдоль вала до середины червяка от середины ступицы муфты Т₁ = 14,0 Н×м.

6.2.2 Определим наибольшие напряжения изгиба и кручения для опасных сечений

Сечение В.

Суммарный изгибающий момент в сечении равен:

М_изΣ = = 163,5 Н×м.

Напряжения изгиба:

σ_из = ,(7.5)

где d_f1 – диаметр впадин витка червяка, м.

σ_из =  = 42,4 МПа.

Напряжения кручения:

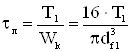(7.6)

где Т₁ – крутящий момент на валу, Н×м.

= 1,80 МПа.

Определим эквивалентное напряжение по энергетической теории прочности и сравним его значение с допустимым:

σ_экв = = 42,5 МПа,

что меньше [σ_n]_-1 = 124 МПа.

Сечение С.

Изгибающий момент в сечении:

М_изг = М_изХ = 25,5 Н×м.

Напряжение изгиба определяется по формуле 8.5

σ_из = = 4,1 МПа.

Напряжение кручения находится по формуле 8.6.

= 1,1 МПа.

Эквивалентное напряжение:

σ_экв = = 4,52 МПа,

что гораздо меньше [σ_n]_-1 = 124 МПа.

6.3 Приближенный расчет тихоходного вала

Примем материал для изготовления вала - сталь 40ХН, для которой σ_в = 920 МПа. Тогда допускаемое напряжение изгиба будет равняться по формуле 7.4.

[σ_n]_-1 = ,

[σ_n]_-1 = 0,43×σ_b+100;

σ_-1 = 0,43×920+100 = 495,6 МПа;

[σ_n]_-1 = = 146 МПа.

6.3.1 Составим схему нагружения вала (рисунок 7.2) в соответствии со схемой действия сил и эскизной компоновки

Строим эпюры изгибающих моментов.

В вертикальной плоскости YOZ (рисунок 7.2 в)

а) определим опорные реакции сил F_t2 и F_k2:

ΣМ_k = 0 - F_t2×70 + F_k2×230 – R_MY×140 = 0;

R_MY == 2776 Н;

ΣМ_M = 0 - R_KY×140 + F_t2×70 + F_k2×90 = 0;

R_KY == 3921 Н

б) проверим правильность определения реакций.

ΣY = R_KY – F_t2 – R_MY + F_k2 =3921 – 4075 - 2776 + 2930 = 0,

т.е. реакции определены верно по величине и по направлению.

в) строим эпюру изгибающих моментов (рисунок 7.2 г), определяя их значения в характерных сечениях вала:

-   в сечении K M= 0;

-   в сечении L M= R_KY×70×10^-3 = 4089×70×10^-3 = 286,2 Н×м;

-   в сечении M M= F_k2×70×10^-3 = 2930×90×10^-3 = 263,7 Н×м;

-   в сечении N M= 0.

Откладываем найденные значения моментов на сжатом волокне вала. В горизонтальной плоскости XOZ (рисунок 7.2 д).

а) определим опорные реакции от действия сил F_r2 и F_a2

ΣМ_k = 0 F_r2×70 – F_a2× - R_MX×140 = 0;

R_MX == 75 Н;

ΣМ_M = 0 - F_r2×50 – F_a2×120 + R_KX×100 = 0;

R_Kx == 1425 Н

б) проверим правильность определения реакций.

ΣX = - R_KX + F_r2 - R_MX = - 1425 + 1500 - 75 = 0,

т.е. реакции определены верно.

в) строим эпюры изгибающих моментов (рисунок 7.2 е), определяя их значения в характерных сечениях вала:

-   в сечении K M= 0;

-   в сечении L M= R_KX×70×10^-3 = 1425×70×10^-3 = 99,75 Н×м;

-   в сечении M M= 0.

Значение моментов от силы F_а2 и R_KX не совпадают по направлению, поэтому откладываем значения момента Mвниз от оси, а значение момента Mвверх из этой точки, т.е. от значения M=99,75 Н×м.

г) проверим правильность определения момента Mот действия сил R_МX.

M= R_МX×70×10^-3 = 5,25 Н×м.

д) строим эпюру крутящих моментов (рисунок 7.2 ж). Передача его происходит вдоль вала до середины червячного колеса:

Т₂ = 550 Н×м.

6.3.2 Вычислим наибольшее напряжение изгиба и кручения для опасных сечений

Сечение L.

Суммарный изгибающий момент

М_изΣ = = 303 Н×м.

Диаметр вала в опасном сечении ослаблен шпоночным пазом. При известных значениях его размеров осевой момент сопротивления W_n и

полярный момент сопротивления W_k определяем согласно формулам:

W_n = 0,1×d³ - ,(7.7)

W_k = 0,2×d³ - ,(7.8)

Для вала d = 48 мм, b = 14 мм, t = 5,5 мм.

Подставив в формулы (8.7) и (8.8) исходные данные, получаем:

W_n = 0,96×10^-5 м³;

W_k = 2,07×10^-5 м³.

Определим напряжение изгиба:

σ_n = =31,6 МПа.

Напряжение кручения:

= 26,6 МПа.

Эквивалентное напряжение:

σ_экв = = 55,9 МПа.

что меньше [σ_n]_-1 = 146 МПа.

Сечение М.

Изгибающий момент в сечении:

М_изг = М_изY = 286,2 Н×м.

Напряжение изгиба:

σ_из = = 68,0 МПа.

Напряжение кручения:

= 65,4 МПа.

Эквивалентное напряжение:

σ_экв = = 132,1 МПа,

что меньше [σ_n]_-1 = 146 МПа.

7 ПОДБОР И РАСЧЕТ ПОДШИПНИКОВ 7.1 Быстроходный вал

Частота вращения вала n₁=1500 об/мин d_n=40мм. Требуемая долговечность подшипников L_n = 3811 час. Схема установки подшипников - в распор. На опоры вала действуют силы

R_Ay=350 H;

R_ax = 424 Н;

F_a1 = 4075 Н;

R_Cy = 350 Н;

R_Cx =755,5 H.

Предварительно примем подшипники роликовые конические средней серии 7308

С=56,0 кН; ℓ = 0,35, у=1,7. Для определения осевых нагрузок на опоры вычислим суммарные реакции опор и приведем схему нагружения вала рис. 8.1

R_a = = 550 Н;

R_с = = 833 Н;

Применительно к схеме получим:

R_z1 = R_A = 550 Η

R_Z2=R_C=833 H

F_a = F_аl = 4075 Η

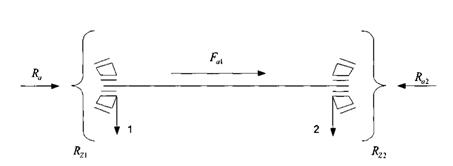
Рисунок 8.1 – Схема нагружения быстроходного вала

Определим осевые составляющие по формуле:

R_s=0,83×ℓ×R_я

R_S1 = 0,83×ℓ×R_Z1 = 0,83×0,35×550 = 160 Η

R_S2 =0,83×ℓ×R_Z2 =0,83×0,35×833 = 242 Η

так как R_S1 < R_S2 и F_a > R_S2 - R_S1 = 242 - 160 = 82 H,

то осевые силы, нагружающие подшипники:

R_a1 =R_S1 = 160 Η,

R_a2 =R_a1 + F_a = 160+ 4075 = 4235 Η.

Сравним отношение  с коэффициентом ℓ и окончательно примем значения коэффициентов x и у.

При == 0,29 <ℓ = 0,35,

x = 1; y = 0.

При == 5,1 > ℓ = 0,35,

x = 0,35; y = 1,7.

Вычислим эквивалентную динамическую нагрузку:

R_Ε=(v·ΧR_я + yR_a)·Κ_Β·Κ_T ,(8.2.)

где σ = 1 - коэффициент вращения, при вращении внутреннего кольца подшипника;

К_Б = 1,1 - коэффициент безопасности

отсюда,

R_E1 = vXR_z1×К_Б×К_т = 1×1×550×1,1×1 = 605 Н,

R_Е2 = (vΧR_я2 + YR_a2)×К_Б×К_т = (1×0,35×833+1,7×4235)×1,1×1 = 8240 Н = 8,24 кН.

Определим расчетную долговечность подшипника при:

L_ioh = 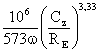,(8,3)

где ω – угловая скорость, с^-1.

L_ioh = 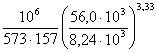= 6540 час,

что больше требуемой долговечности

L_h = 3811 час.

Определим динамическую грузоподъемность:

С_гр = R_Е×,(8.4)

тогда С_гр = 8,24×= 47,6 кН,

что меньше С_z = 56 кН.

подшипник 7211 пригоден.

7.2 Тихоходный вал

Частота вращения вала, n₂ = 95,5 об/мин, угловая скорость ω₂ = 10 с^-1, d_n = 35 мм. Схема установки подшипников - в распор. На опоры вала действуют силы:

R_ky = 3921 Η;

R_my=2776 H;

R_kx = 1425 Η;

R_mx = 75 Η;

F_a2 = 700 Η.

Определим суммарную реакцию опор:

R_x = = 4170 Н;

R_m = = 2777Н;

Предварительно примем подшипники роликовые конической серии 7207.

Для него выпишем: C_Z=32,5 кH, ℓ = 0,37, у = 1,62.

Для определения осевых нагрузок на опоры приведем схему нагружения вала рис.8.2 к виду представленному на рис.6.4а [8,с.102]

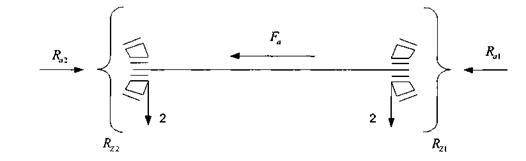
Рисунок 8.2 – Схема нагружения тихоходного вала

Применительно к схеме получим:

R_Z1=R_m=2777 Н;

R_Z2 = R_x =4170 Η;

F_a = F_a2 = 700 Η.

Определим осевые составляющие по формуле 8.1

R_S1 = 0,83×ℓ×R_Z1 = 0,83×0,37×2777 = 853 Η

R_S2 =0,83×ℓ×R_Z2 =0,83×0,37×4170 = 1280 Η

так как R_S1 < R_S2 и F_a > R_S2 - R_S1 = 1280 – 853 = 427 H,

то осевые силы, нагружающие подшипники:

R_a1 =R_S1 = 853 Η,

R_a2 =R_a1 + F_a = 853+700 = 1553 Η.

Сравним отношение  с коэффициентом ℓ и окончательно примем значения коэффициентов x и у.

При == 0,307 <ℓ = 0,37,

x = 1; y = 0.

При == 0,37 < ℓ = 0,37,

x = 1; y = 0.

Вычислим эквивалентную динамическую нагрузку по формуле (9.2.):

R_Ε1=v·x×R_Z1×Κ_Β·Κ_T = 1×1×2777×1,1×1 = 3055 Н,

R_Ε2=v·x×R_Z2×Κ_Β·Κ_T = 1×1×4170×1,1×1 = 4587 Н = 4,59 кН,

Определим расчетную долговечность подшипников в опоре 2 по формуле (8.3):

L_ioh = 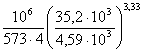= 385420час,

Что больше требуемой долговечности

L_h = 3810,6 час.

Определим динамическую грузоподъемность по формуле (8.4):

С_гр = 4,59×= 8,8 кН,

что меньше С_z = 35,2,

подшипник 7207 пригоден.

ЛИТЕРАТУРА

1 Каталог электродвигателей постоянного тока серии 2П. - М., 1991.- 250 с.

2 Дунаев П.Ф. Детали машин. Курсовое проектирование. - М., 1990. - 462 с.

3 Иванов М.И. Детали машин. - М., 1991. - 532 с.