Навигация
Исследование устойчивости САУ по логарифмическому критерию
4.3 Исследование устойчивости САУ по логарифмическому критерию
Для исследования САУ по логарифмическому критерию строим логарифмические амплитудно-частотную (ЛАЧХ) и фазочастотную (ЛФЧХ) характеристики разомкнутой САУ. Для этого определяем частоты сопряжения
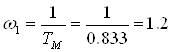 с-1;
с-1;
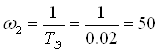 с-1;
с-1;
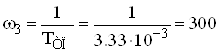 с-1;
с-1;
коэффициент усиления САУ
![]() дб.
дб.
наклон первой асимптоты — -20 дб/дек;
наклон второй изменяется на -20дб/дек и составляет — -40 дб/дек;
наклон третьей изменяется на -20 дб/дек и составляет — -60 дб/дек;
наклон четвёртой изменяется на -20 дб/дек и составляет — -80 дб/дек;
Для построения ЛФЧХ используем данные табл. 2. Из характеристик очевидно, что система неустойчива, так как ЛФЧХ пересекает ось w раньше, чем ЛАЧХ.
4.4 Сопоставление результатов исследования устойчивости различными методами
Рассмотренные выше критерии устойчивости дали один и тот же результат. Однако, с точки зрения практического использования они неравноценны.
Критерий Гурвица позволяет получить только качественное суждение о характере процесса регулирования, т.е. устойчивость, устойчив или нет процесс; но он является наиболее точным. А также данный метод позволяет определить предельный коэффициент усиления САУ.
Частотный критерий Найквиста применяется тогда, когда трудно получить уравнения всех звеньев, но можно получить экспериментально - фазовые их характеристики. Устойчивость по данному методу определяется по тому, как АФЧХ охватывает точку с координатами (-1; j0).
Кроме того, расположение ЛФЧХ еще не дает прямого ответа, устойчива ли система, что требует дополнительных исследований.
При использовании логарифмических частотных характеристик оценка устойчивости системы производится проще, т.е. по их виду можно заключить, устойчива система или нет; но можно получить противоречивые показания, так как мы используем приближенную ЛАЧХ, вместо точной.
5. Синтез последовательного корректирующего устройства
5.1 Расчет и построение желаемой логарифмической частотной характеристики
Синтез последовательного корректирующего устройства выполним методом логарифмических характеристик.
В дальнейшем будем предполагать, что САУ состоит из измерительного устройства, исполнительного устройства и объекта управления с общей передаточной функцией W(S) и последовательного корректирующего устройства с передаточной функцией Wку(S).
При рассмотрении желаемой логарифмической частотной характеристики (ЖЛАЧХ) выделим четыре области:
а) область очень низких частот (0, ![]() ).
).
Наклон характеристики составляет — -20 дб/дек, по количеству интегрирующих звеньев;
б) область низких частот ( ![]() ,
,![]() ).
).
Наклон составляет - 40 дб/дек, по количеству апериодических звеньев с постоянной времени
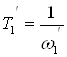 ;
;
в) область средних частот (![]() ,
,![]() ).
).
Наклон на частоте среза ![]() составляет – 20 дб/дек для обеспечения необходимых запасов устойчивости.
составляет – 20 дб/дек для обеспечения необходимых запасов устойчивости.
г) область высоких частот (![]() ,¥ ).
,¥ ).
Наклон существенно не влияет на качество САУ, поэтому выберем его по исходной ЛАЧХ.
Рассчитаем параметры ЖЛАЧХ:
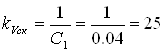 ;
; ![]() дб.
дб.
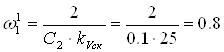 с-1
с-1
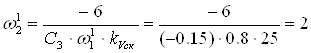 с-1
с-1
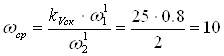 с-1
с-1
По полученным данным и с учётом предъявляемых требований строим ЖЛАЧХ.
5.2 Выбор последовательного корректирующего устройства и расчет его параметров
Решим задачу синтеза последовательного корректирующего устройства. Для этого из ЖЛАЧХ геометрически вычтем ЛАЧХ не скорректированной системы. Полученная характеристика представляет собой ЛАЧХ корректирующего устройства.
По виду ЛАЧХ корректирующего устройства определим его передаточную функцию, схему и параметры. Приведенной ЛАЧХ корректирующего устройства соответствует ниже представленная схема:
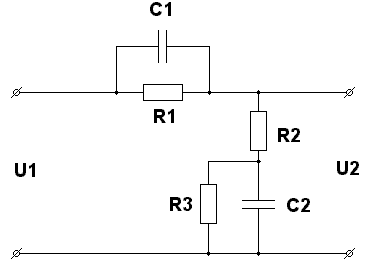
Рис. 4 Схема корректирующего устройства
![]() ;
; ![]() .
.
Передаточная функция устройства:
Wск(S) = 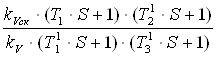 ;
;
где ![]() с;
с; ![]() с;
с; ![]() с;
с; ![]() с;
с;
kVск – коэффициент усиления скорректированной САУ;
kV – коэффициент усиления исходной САУ.
Количество сомножителей вида (![]() ) в числителе соответствует количеству переходов +20дб/дек, а в знаменателе — -20дб/дек. Постоянные времени
) в числителе соответствует количеству переходов +20дб/дек, а в знаменателе — -20дб/дек. Постоянные времени ![]() , определяются соответствующими частотами сопряжения на ЛАЧХ корректирующего устройства.
, определяются соответствующими частотами сопряжения на ЛАЧХ корректирующего устройства.
Рассчитаем параметры корректирующего устройства:
примем ![]() мФ, тогда
мФ, тогда
![]() Ом;
Ом;
примем![]() Ом, тогда
Ом, тогда
![]() мФ.
мФ.
Структурную схему скорректированной САУ можно представить в виде:

Рис. 5 Структурную схему скорректированной САУ
6. Расчет и построение переходной характеристики скорректированной САУ
6.1 Расчет фазовой частотной характеристики скорректированной САУ
Расчет ФЧХ скорректированной САУ произведем по звеньям
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
а результаты занесем в табл.3. По рассчитанным данным построим ЛФЧХ скорректированной САУ. Из характеристик, очевидно, что система устойчива.
Запас по фазе – 57,5°, по амплитуде – 12 дб.
Табл. 3
| Звенья | w,с-1 | ||||||||
| 0 | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | |
| jа1(w) | 0 | -68,2 | -80,9 | -85,4 | -87,7 | -89,1 | -89,5 | -89,7 | -89,8 |
| jа2(w) | 0 | -2,6 | -6,56 | -12,95 | -24,7 | -49,0 | -66,5 | -73,8 | -77,7 |
| jф1(w) | 0 | 58,9 | 76,5 | 83,1 | 86,6 | 88,6 | 89,3 | 89,5 | 89,65 |
| jф2(w) | 0 | 45,0 | 68,2 | 78,7 | 84,3 | 87,7 | 88,85 | 89,2 | 89,4 |
| jåж(w) | 0 | 33,1 | 57,2 | 63,45 | 58,5 | 38,2 | 22,15 | 15,2 | 11,55 |
| jå(w) | -90 | -118,6 | -116 | -123 | -143,7 | -194,9 | -239 | -262,4 | -277,9 |
7. Определение показателей качества замкнутой скорректированной САУ
По построенной переходной характеристике скорректированной системы, определяем основные показатели качества: перерегулирование ![]() , время первого согласования
, время первого согласования ![]() , время достижения первого максимума
, время достижения первого максимума ![]() , время регулирования
, время регулирования ![]() , число колебаний N, а также запасы по фазе и амплитуды:
, число колебаний N, а также запасы по фазе и амплитуды:
![]() с,
с,
![]() с,
с,
![]() с,
с,
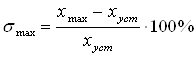 ;
;
![]() ,
,
Азап = 12 дБ,
jзап = 57,50.
Похожие работы
... поведение регулируемой величины. Управляющее воздействие вырабатывается устройством управления (УУ). Совокупность взаимодействующих управляющего устройства и управляемого объекта образует систему автоматического управления. Система автоматического управления (САУ) поддерживает или улучшает функционирование управляемого объекта. В ряде случаев вспомогательные для САУ операции (пуск, остановка, ...
... . Таким образом, необходимость автоматизации технологических процессов очевидна и есть необходимость научиться рассчитывать параметры систем автоматического управления (САУ), для последующего применения своих знаний на практике. В курсовой работе произведен анализ динамических свойств заданной структурной схемы САУ с составлением и анализом математических моделей объектов управления. 2. Анализ ...
... можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость. Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением. Построение области ...
... для переходной функции (22) Подставив эти выражения в формулу для h(t) и выполнив преобразования, получим связь между переходной функцией и ВЧХ: (23) Логарифмические частотные характеристики САУ Исследование систем существенно упрощается при использовании не обычных, а логарифмических частотных характеристик. При этом натуральная логарифмическая амплитудная и фазовая частотные ...


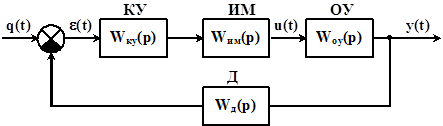
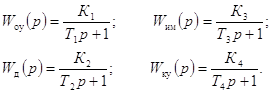

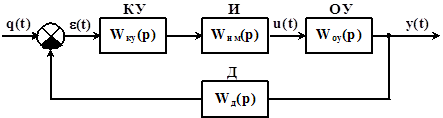
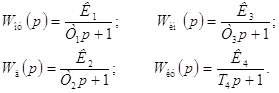

0 комментариев