Навигация
1.2. Методы решения ЗК
1.2.1. Жадный алгоритм
Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.
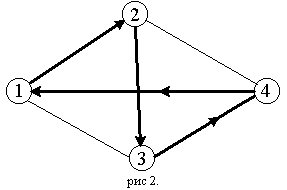
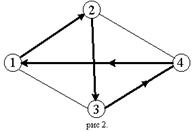
Посмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь он превратится в стратегию «иди в ближайший (в который еще не входил) город». Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рис. 2, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм «иди вы ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
В пользу процедуры «иди в ближайший» можно сказать лишь то, что при старте из одного города она не уступит стратегии «иди в дальнейший».
Как видим, жадный алгоритм ошибается. Можно ли доказать, что он ошибается умеренно, что полученный им тур хуже минимального, положим, в 1000 раз? Мы докажем, что этого доказать нельзя, причем не только для жадного логарифма, а для алгоритмов гораздо более мощных. Но сначала нужно договориться, как оценивать погрешность неточных алгоритмов, для определенности, в задаче минимизации. Пусть fB - настоящий минимум, а fA - тот квазиминимум, который получен по алгоритму. Ясно, что fA/ fB≥1, но это – тривиальное утверждение, что может быть погрешность. Чтобы оценить её, нужно зажать отношение оценкой сверху:
| fA/fB ≥1+ nε, | (5) |
где, как обычно в высшей математике, ε≥0, но, против обычая, может быть очень большим. Величина ε и будет служить мерой погрешности. Если алгоритм минимизации будет удовлетворять неравенству (5), мы будем говорить, что он имеет погрешность ε.
Предположим теперь, что имеется алгоритм А решения ЗК, погрешность которого нужно оценить. Возьмем произвольный граф G (V,E) и по нему составим входную матрицу ЗК:
| С[i,j]={ | 1,если ребро (i,j) принадлежит Е |
| 1+nε в противном случае |
Если в графе G есть гамильтонов цикл, то минимальный тур проходит по этому циклу и fB = n. Если алгоритм А тоже всегда будет находить этот путь, то по результатам алгоритма можно судить, есть ли гамильтонов цикл в произвольном графе. Однако, непереборного алгоритма, который мог бы ответить, есть ли гамильтонов цикл в произвольном графе, до сих пор никому не известно. Таким образом, наш алгоритм А должен иногда ошибаться и включать в тур хотя бы одно ребро длины 1+nε. Но тогда fA³(n-1)+(1+nε) так что fA/fB=1+nε т.е. превосходит погрешность ε на заданную неравенством (5). О величине ε в нашем рассуждении мы не договаривались, так что ε может быть произвольно велик.
Таким образом доказана следующая теорема.
Либо алгоритм А определяет, существует ли в произвольном графе гамильтонов цикл, либо погрешность А при решении ЗК может быть произвольно велика.
Это соображение было впервые опубликовано Сани и Гонзалесом в 1980 г. Теорема Сани-Гонзалеса основана на том, что нет никаких ограничений на длину ребер. Теорема не проходит, если расстояния подчиняются неравенству треугольника (4).
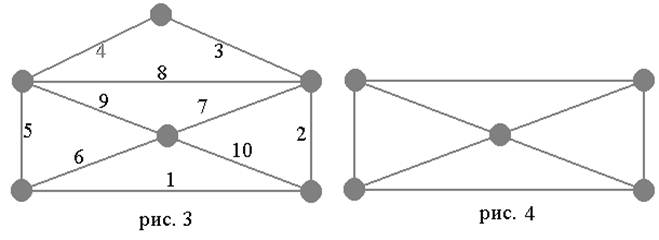Если оно соблюдается, можно предложить несколько алгоритмов с погрешностью 12. Прежде, чем описать такой алгоритм, следует вспомнить старинную головоломку. Можно ли начертить одной линией открытый конверт? Рис.2 показывает, что можно (цифры на отрезках показывают порядок их проведения). Закрытый конверт (рис.3.) одной линией нарисовать нельзя и вот почему. Будем называть линии ребрами, а их перекрестья – вершинами.
Когда через точку проводится линия, то используется два ребра – одно для входа в вершину, одно – для выхода. Если степень вершины нечетна – то в ней линия должна начаться или кончиться. На рис. 3 вершин нечетной степени две: в одной линия начинается, в другой – кончается. Однако на рис. 4 имеется четыре вершины степени три, но у одной линии не может быть четыре конца. Если же нужно прочертить фигуру одной замкнутой линией, то все ее вершины должны иметь четную степень.
Верно и обратное утверждение: если все вершины имеют четную степень, то фигуру можно нарисовать одной незамкнутой линией. Действительно, процесс проведения линии может кончиться, только если линия придет в вершину, откуда уже выхода нет: все ребра, присоединенные к этой вершине (обычно говорят: инцидентные этой вершине), уже прочерчены. Если при этом нарисована вся фигура, то нужное утверждение доказано; если нет, удалим уже нарисованную часть G’. После этого от графа останется одна или несколько связных компонент; пусть G’ – одна из таких компонент. В силу связности исходного графа G, G’ и G’’ имеют хоть одну общую вершину, скажем, v. Если в G’’ удалены какие-то ребра, то по четному числу от каждой вершины. Поэтому G’’ – связный и все его вершины имеют четную степень. Построим цикл в G’’ (может быть, не нарисовав всего G’’) и через v добавим прорисованную часть G’’ к G’. Увеличивая таким образом прорисованную часть G’, мы добьемся того, что G’ охватит весь G.
Эту задачу когда-то решил Эйлер, и замкнутую линию, которая покрывает все ребра графа, теперь называю эйлеровым циклом. По существу была доказана следующая теорема.
Эйлеров цикл в графе существует тогда и только тогда, когда (1) граф связный и (2) все его вершины имеют четные степени.
Похожие работы
... важным элементом образования специалистов, связанных с её применением при решении задач, возникающих в приложениях. Поэтому нам представляется, что технология решения задач дискретного программирования должна стать одной из важных составных частей современного математического образования для специалистов по прикладной математике. Дискретные оптимизационные задачи можно решать двумя методами: ...
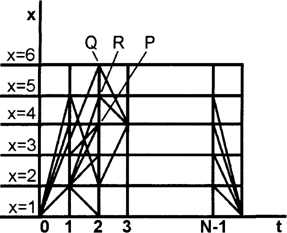
... и j входит в выражение (1) один и только один раз. Функция является, таким образом, аддитивной - она представима в виде суммы слагаемых, однако сама задача - задача отыскания минимума l - в силу ограничения (a) не является аддитивной и не удовлетворяет принципу оптимальности. Рис.1. Рассмотрим плоскость t, х, где t - дискретный аргумент, принимающий значения 0, 1, 2, . . . , N, ...
... с помощью Visual C++. Описание алгоритма В программе содержится рекурсивная функция, которая обеспечивает перебор возможных путей для поиска самого короткого. Именно здесь заключен алгоритм решения задачи «коммивояжера». Рассмотрим его подробнее: 1. Для каждого города (i = от 1 до n), где мы еще не были. 2. Допустим, что мы пришли в какой-то город i. Помечаем его, что мы здесь уже ...
... (4) до тех пор пока не останется последний разрешающий элемент. В итоге искомый маршрут будет проходить через пункты: А – Б – Г – Д – В – А min z = 16+21+16+12+13 = 78 Раздел 2. Определение рационального варианта размещения производственных предприятий (на примере АБЗ). Постановка задачи: В 2000г планируется осуществить ремонт и реконструкцию дорожной сети некоторого района. ...
0 комментариев