Навигация
1.2.4. Алгоритм Дейкстры
Одним из вариантов решения ЗК является вариант нахождения кратчайшей цепи, содержащей все города. Затем полученная цепь дополняется начальным городом – получается искомый тур.
Можно предложить много процедур решения этой задачи, например, физическое моделирование. На плоской доске рисуется карта местности, в города, лежащие на развилке дорог, вбиваются гвозди, на каждый гвоздь надевается кольцо, дороги укладываются верёвками, которые привязываются к соответствующим кольцам. Чтобы найти кратчайшее расстояние между i и k, нужно взять I в одну руку и k в другую и растянуть. Те верёвки, которые натянутся и не дадут разводить руки шире и образуют кратчайший путь между i и k. Однако математическая процедура, которая промоделирует эту физическую, выглядит очень сложно. Известны алгоритмы попроще. Один из них – алгоритм Дейкстры, предложенный Дейкстрой ещё в 1959г. Этот алгоритм решает общую задачу:
В ориентированной, неориентированной или смешанной (т. е. такой, где часть дорог имеет одностороннее движение) сети найти кратчайший путь между двумя заданными вершинами.
Алгоритм использует три массива из n (= числу вершин сети) чисел каждый. Первый массив a содержит метки с двумя значениями: 0 (вершина ещё не рассмотрена) и 1 (вершина уже рассмотрена); второй массив b содержит расстояния – текущие кратчайшие расстояния от vi до соответствующей вершины; третий массив c содержит номера вершин – k-й элемент ck есть номер предпоследней вершины на текущем кратчайшем пути из vi в vk. Матрица расстояний Dik задаёт длины дуг dik; если такой дуги нет, то dik присваивается большое число Б, равное «машинной бесконечности».
Теперь можно описать:
Алгоритм Дейкстры
1(инициализация).
В цикле от одного до n заполнить нулями массив а; заполнить числом i массив с: перенести i-тую строку матрицы D в массив b;
a[i]:=1; c[i]:=0; {i-номер стартовой вершины}
2(общий шаг).
Найти минимум среди неотмеченных (т. е. тех k, для которых a[k]=0); пусть минимум достигается на индексе j, т. е. bj£bk; a[j]:=1;
| 0 | 23 | 12 | ∞ | ∞ | ∞ | ∞ | ∞ |
| 23 | 0 | 25 | ∞ | 22 | ∞ | ∞ | 35 |
| 12 | 25 | 0 | 18 | ∞ | ∞ | ∞ | ∞ |
| ∞ | ∞ | 18 | 0 | ∞ | 20 | ∞ | ∞ |
| ∞ | 22 | ∞ | ∞ | 0 | 23 | 14 | ∞ |
| ∞ | ∞ | ∞ | 20 | 23 | 0 | 24 | ∞ |
| ∞ | ∞ | ∞ | ∞ | 14 | 24 | 0 | 16 |
| ∞ | 35 | ∞ | ∞ | ∞ | ∞ | 16 | 0 |
| табл. 12 | |||||||
если bk>bj+djk то (bk:=bj+djk; ck:=j) {Условие означает, что путь vi..vk длиннее, чем путь vi..vj,vk . Если все a[k] отмечены, то длина пути vi..vk равна b[k]. Теперь надо перечислить вершины, входящие в кратчайший путь}
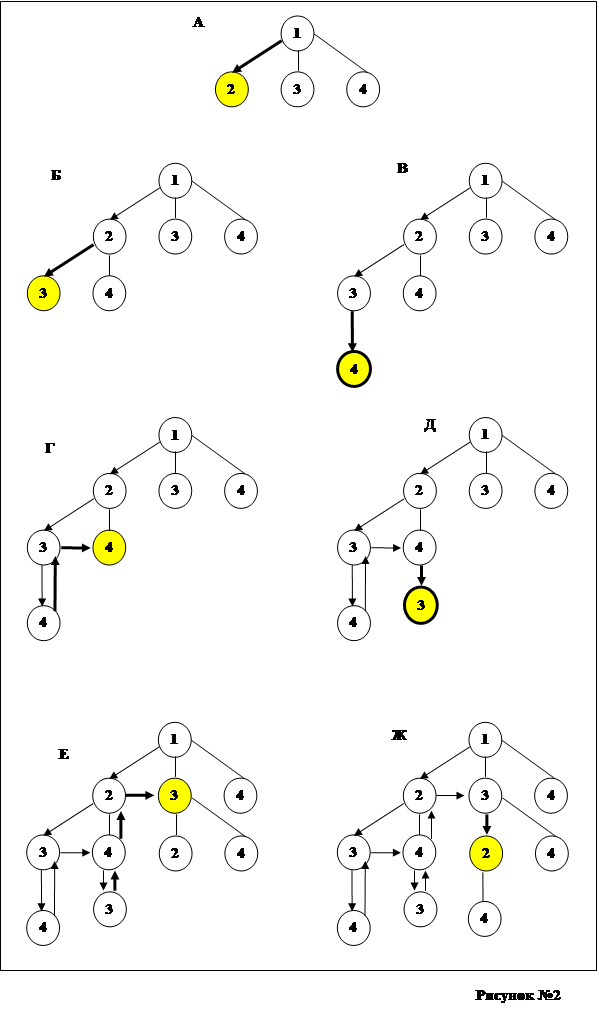
3(выдача ответа).
{Путь vi..vk выдаётся в обратном порядке следующей процедурой:}
3.1. z:=c[k];
3.2. Выдать z;
3.3. z:=c[z]; Если z = 0, то конец, иначе перейти к 3.2.
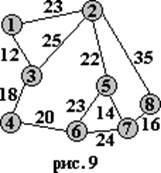
Для выполнения алгоритма нужно n раз просмотреть массив b из n элементов, т. е. алгоритм Дейкстры имеет квадратичную сложность. Проиллюстрируем работу алгоритма Дейкстры численным примером (для большей сложности, считаем, что некоторые города (вершины) i,j не соединены между собой, т. е. D[i,j]=∞). Пусть, например, i=3. Требуется найти кратчайшие пути из вершины 3. Содержимое массивов a,b,c после выполнения первого пункта показано на табл. 12:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| a | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| b | 12 | 25 | 0 | 18 | ∞ | ∞ | ∞ | ∞ | |
| c | 3 | 3 | 0 | 3 | 3 | 3 | 3 | 3 | |
| табл. 13 |
| ||||||||
Очевидно, содержимое таблицы меняется по мере выполнения общего шага. Это видно из следующей таблицы:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| min bk=12 | a | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| b | 12 | 25 | 0 | 18 | ∞ | ∞ | ∞ | ∞ | |
| c | 3 | 3 | 0 | 3 | 3 | 3 | 3 | 3 | |
| min bk=18 | a | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| b | 12 | 25 | 0 | 18 | ∞ | 38 | ∞ | ∞ | |
| c | 3 | 3 | 0 | 3 | 3 | 4 | 3 | 3 | |
| min bk=25 | a | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| b | 12 | 25 | 0 | 18 | 47 | 38 | ∞ | 60 | |
| c | 3 | 3 | 0 | 3 | 2 | 4 | 3 | 2 | |
| min bk=38 | a | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| b | 12 | 25 | 0 | 18 | 47 | 38 | 62 | 60 | |
| c | 3 | 3 | 0 | 3 | 2 | 4 | 6 | 2 | |
| min bk=47 | a | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| b | 12 | 25 | 0 | 18 | 47 | 38 | 61 | 60 | |
| c | 3 | 3 | 0 | 3 | 2 | 4 | 5 | 2 | |
| min bk=60 | a | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| b | 12 | 25 | 0 | 18 | 47 | 38 | 61 | 60 | |
| c | 3 | 3 | 0 | 3 | 2 | 4 | 5 | 2 |
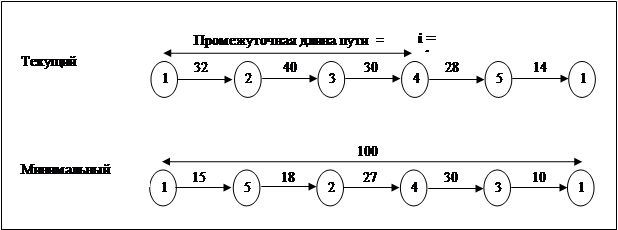
Таким образом, для решения ЗК нужно n раз применить алгоритм Дейкстры следующим образом.
Возьмём произвольную пару вершин
j,k. Исключим непосредственное ребро C[j,k]. С помощью алгоритма Дейкстры найдём кратчайшее расстояние между городами j..k. Пусть это расстояние включает некоторый город m. Имеем часть тура j,m,k. Теперь для каждой пары соседних городов (в данном примере – для j,m и m,k) удалим соответственное ребро и найдём кратчайшее расстояние. При этом в кратчайшее расстояние не должен входить уже использованный город.
Далее аналогично находим кратчайшее расстояние между парами вершин алгоритмом Дейкстры, до тех пор, пока все вершины не будут задействованы. Соединим последнюю вершину с первой и получим тур. Чаще всего это последнее ребро оказывается очень большим, и тур получается с погрешностью, однако алгоритм Дейкстры можно отнести к приближённым алгоритмам.
Похожие работы
... важным элементом образования специалистов, связанных с её применением при решении задач, возникающих в приложениях. Поэтому нам представляется, что технология решения задач дискретного программирования должна стать одной из важных составных частей современного математического образования для специалистов по прикладной математике. Дискретные оптимизационные задачи можно решать двумя методами: ...
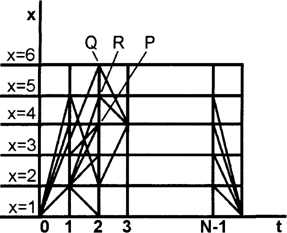
... и j входит в выражение (1) один и только один раз. Функция является, таким образом, аддитивной - она представима в виде суммы слагаемых, однако сама задача - задача отыскания минимума l - в силу ограничения (a) не является аддитивной и не удовлетворяет принципу оптимальности. Рис.1. Рассмотрим плоскость t, х, где t - дискретный аргумент, принимающий значения 0, 1, 2, . . . , N, ...
... с помощью Visual C++. Описание алгоритма В программе содержится рекурсивная функция, которая обеспечивает перебор возможных путей для поиска самого короткого. Именно здесь заключен алгоритм решения задачи «коммивояжера». Рассмотрим его подробнее: 1. Для каждого города (i = от 1 до n), где мы еще не были. 2. Допустим, что мы пришли в какой-то город i. Помечаем его, что мы здесь уже ...
... (4) до тех пор пока не останется последний разрешающий элемент. В итоге искомый маршрут будет проходить через пункты: А – Б – Г – Д – В – А min z = 16+21+16+12+13 = 78 Раздел 2. Определение рационального варианта размещения производственных предприятий (на примере АБЗ). Постановка задачи: В 2000г планируется осуществить ремонт и реконструкцию дорожной сети некоторого района. ...

0 комментариев