Цифровая обработка сигналов и её использование в системах распознавания речи
Прямое и обратное г-преобразование
Спектральный анализ
Основы цифровой фильтрации
Особенности акустической фонетики и её учёт при обработке речевых сигналов
Распространение звуков
Реализация систем распознавания речи
Кодирование речи на основе линейного предсказания
Цифровая обработка речи в системах речевого общения человека с машиной
Системы распознавания дикторов
Обзор существующих систем распознавания речи
Основные функции, необходимые для воспроизведения звука
Реализация программного обеспечения для записи, воспроизведения и анализа звукового сигнала
Реализация функции распознавания голосовых команд голосового управления промышленным роботом
Навигация
Спектральный анализ
Разработка программного обеспечения для голосового управления трехмерными моделями функционирования промышленных роботов
158991
знак
11
таблиц
10
изображений
1.1.4 Спектральный анализ
Спектральный анализ – это метод обработки сигналов, который позволяет выявить частотный состав сигнала. Поскольку анализируемые сигналы во многих случаях имеют случайный характер, то важную роль в спектральном анализе играют методы математической статистики. Частотный состав сигналов определяют путем вычисления оценок спектральной плотности мощности (СПМ). Задачами вычисления СПМ являются обнаружение гармонических составляющих в анализируемом сигнале и оценивание их параметров. Для решения указанных задач требуется соответственно высокая разрешающая способность по частоте и высокая статистическая точность оценивания параметров. Эти два требования противоречивы. Аргументы в пользу выбора высокого разрешения или высокой точности оценки СПМ зависят от того, что интересует исследователя: устойчивые оценки в пределах всего диапазона частот или высокая степень обнаруживаемости периодических составляющих.
Все методы цифрового спектрального анализа можно разделить, на две группы [6-7]: классические методы, базирующиеся на использовании преобразований Фурье, и методы параметрического моделирования, в которых выбирается некоторая линейная модель формирующего фильтра и оцениваются его параметры. К первой группе относят корреляционный и периодограммные методы. Ко второй группе относят методы оценивания СПМ на основе авторегрессии скользящего среднего и др.
Периодограммный метод обеспечивает вычисление оценки СПМ непосредственно по числовой последовательности х[nТ0], формируемой путем дискретизации стационарного эргодического случайного процесса x(t). Периодограммная оценка СПМ равна [6-7]
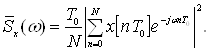(1.18)
Выражение (1.18) соответствует возможности вычисления СПМ с помощью преобразования Фурье непосредственно по реализации исходного сигнала.
Вычисленная с помощью (1.18) оценка СПМ является несостоятельной, т.е. с увеличением N она не улучшается. Для получения состоятельной оценки ее необходимо сглаживать. Кроме этого, при выполнении преобразования Фурье последовательности х[nТ0] конечной длины /V происходит «размывание» спектра, которое также оказывает влияние на состоятельность оценки СПМ.
Ограничение последовательности х[nТ0] конечным числом значений равносильно умножению исходной бесконечной последовательности х0 [nТ0] на другую последовательность
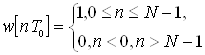
(1.19)
которую называют прямоугольным окном. Тогда можно записать
(1.20)
Преобразование Фурье последовательности х[nТ0] равно свертке преобразований Фурье последовательности х0 [nТ0] и прямоугольного окна w[nТ0]
(1.21)
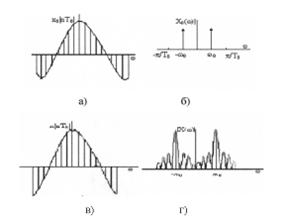
Рисунок 1.2 – Размывание спектра: (а – исходная бесконечная последовательность; б – модуль преобразования Фурье от х0 [nТ0]; в - последовательность х0 [nТ0], умноженная на прямоугольное окно; г - модуль преобразования Фурье последовательности х[nТ0])
При выборе оконных функций используются следующие параметры: ширина основного лепестка, максимальный уровень боковых лепестков, скорость спадания уровня боковых лепестков [6,7,10].
Здесь ширина основного лепестка определена на уровне 3 дБ ниже его максимума и измерена в единицах разрешения преобразования Фурье, т.е. 2π/N, где N - длина окна.
Для повышения состоятельности оценки (1.18) выполняют её сглаживание. Имеется несколько методов сглаживания: Даньелла, Бартлетта, Уэлча [6,7].
Метод Даньелла основан на осреднении значений СПМ в пределах смежных спектральных частот.
В соответствии с методом Бартлетта состоятельность оценки СПМ повышают усреднением оценок СПМ коротких реализаций, полученных из
одной реализации длиной N отсчетов. Пусть дана реализация длиной N отсчетов. Она разбивается на ns неперекрывающихся сегментов, длиной Ns=N/s отсчетов. Для каждого сегмента по формуле (1.18) вычисляется выборочная оценка СПМ. Сглаженная оценка СПМ получается путем усреднения по всем n, сегментам
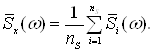(1.30)
Если последовательность х[n] представляет нормальный стационарный эргодический процесс, то сглаженная оценка имеет дисперсию обратно пропорциональную числу сегментов n.
Спектральное разрешение оценки задается приближенным равенством
(1.31)
В методе Уэлча подход Бартлетта применяется к перекрывающимся сигментам исходной последовательности х[n], и каждый сегмент взвешивается с помощью оконной функции для уменьшения смещения оценок из-за эффекта «просачивания» энергии в боковые лепестки. Цель перекрытия сегментов - увеличить число усредняемых участков при фиксированной длине последовательности и тем самым повысить точность оценок СПМ. Метод Уэлча - один из самых распространенных периодограммных методов [6,7].
Обозначим через 
величину сдвига между сегментами, которая должна удовлетворять условию 
, где 
- максимальное имя корреляции анализируемого процесса. При выполнении этого условия получим p=int[(N-Ns)/+l]слабо коррелированных сегментов. Отсчеты каждого сегмента взвешиваются окном w[n]
(1.32)
Выборочное значение СПМ сегмента р оценивается по формуле
(1.33)
где
(1.34)
(1.35)
Сглаженная оценка периодограммы Уэлча вычисляется по формуле
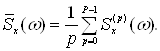(1.36)
Введение перекрытия сегментов в методе Уэлча позволяет уменьшить изменчивость оценки СПМ, Так же как и в методе Бартлетта, дисперсия оценки СПМ по методу Уэлча обратно пропорциональна числу сегментов, но благодаря большему числу сегментов, значение дисперсии будет меньше.
Похожие работы
... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...
... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники 1. Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...
... информация должна поступать в декодер при восстановлении звукового сигнала. Декодер преобразует серию сжатых мгновенных спектров сигнала в обычную цифровую волновую форму. Audio MPEG - группа методов сжатия звука, стандартизованная MPEG (Moving Pictures Experts Group - экспертной группой по обработке движущихся изображений). Методы Audio MPEG существуют в виде нескольких типов - MPEG-1, MPEG-2 и ...
... с применением полиграфических компьютерных технологий? 10. Охарактеризуйте преступные деяния, предусмотренные главой 28 УК РФ «Преступления в сфере компьютерной информации». РАЗДЕЛ 2. БОРЬБА С ПРЕСТУПЛЕНИЯМИ В СФЕРЕ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ ГЛАВА 5. КОНТРОЛЬ НАД ПРЕСТУПНОСТЬЮВ СФЕРЕ ВЫСОКИХ ТЕХНОЛОГИЙ 5.1 Контроль над компьютерной преступностью в России Меры контроля над ...
0 комментариев