Реализация систем распознавания речи

2. Реализация систем распознавания речи

2.1 Гомоморфная обработка речи

Речевой сигнал на коротких интервалах можно рассматривать как отклик системы с медленно меняющимися параметрами на периодическое или шумовое возбуждение. Это означает, что во временной области дискретный сигнал у(n) представляется результатом свертки функции возбуждения х(n) с импульсной реакцией голосового тракта п(п). Гомоморфная обработка речи сводится к решению обратной задачи — имея речевой сигнал у(n)=х(n)*h(n), можно получить параметры сигналов, участвующих в свертке. Эта задача называется иногда задачей обратной свертки или развертки.

Смысл гомоморфной системы анализа становится более понятным, если учесть, что в частотной области речевой сигнал представляется произведением спектра сигнала возбуждения и передаточной функции частотной характеристики голосового тракта, учитывающего спектральные свойства излучателя. Это означает, что в спектре речевого сигнала содержится информация о спектре сигнала возбуждения и передаточной функции голосового тракта. Гомоморфная обработка сигнала — это способ извлечь информацию об основном тоне и формантных частотах на основании преобразований сигнала, которые будут описаны далее.

Если произвести кратковременное дискретное преобразование Фурье (т.е. получить динамический спектр речевого сигнала), а затем прологарифмировать спектральные составляющие динамического спектра, то каждый спектральный отсчет можно рассматривать как сумму логарифмов спектра сигнала возбуждения и частотной характеристики речевого тракта (по свойству логарифмической функции логарифм произведения равен сумме логарифмов сомножителей). Обратное дискретное преобразование Фурье прологарифмированного спектра позволяет вновь перейти к анализу сигнала во временной области. Сигнал, полученный в результате обратного дискретного преобразования Фурье прологарифмированного спектра, называется кепстром входного сигнала, равного сумме кепстров сигналов возбуждения и составляющих, обусловленных особенностями речеобразующего тракта. В результате подобных преобразований дискретный речевой сигнал, представляющий собой свертку сигнала возбуждения и импульсного отклика фильтра, моделирующего голосовой тракт, приближенно преобразуется в сложение кепстров.

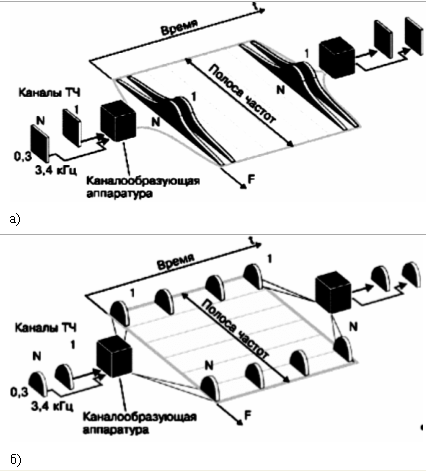
Логарифм кратковременного спектра вокализованных звуков содержит медленно меняющуюся составляющую, обусловленную передаточными свойствами голосового тракта, и быстро меняющуюся периодическую составляющую, которая вызывается периодическим сигналом возбуждения (рис. 2.1а). Для невокализованной речи прологарифмированный спектр носит характер, показанный на рис.2.1б. Спектр содержит случайную составляющую с быстрыми изменениями.

Кепстры отрезков вокализованной и невокализованной речи (рис. 2.2) показывают, что медленно меняющаяся часть прологарифмированных значений кратковременного спектра представлена составляющими кепстра в области малых времен. Быстро меняющаяся периодическая составляющая прологарифмированного спектра, соответствующая частоте основного тона, в кепстре вокализованной речи проявляется в виде резкого пика, расположенного от начала координат на расстоянии, равном периоду основного тона. Кепстр невокализованной речи (рис. 2.2б) таких пиков не имеет.

Если кепстр перемножить на подходящую функцию окна, например прямоугольное окно, пропускающее только начальные участки кепстра (которые соответствуют области малых времен и отражают относительно медленно меняющиеся параметры голосового тракта), а затем вычислить дискретное преобразование Фурье результирующего взвешенного кепстра, то получим сглаженный спектр сигнала.

Он отражает резонансные свойства тракта, позволяя оценивать частоты и полосы формант. Наличие или отсутствие ярко выраженного пика в области, соответствующей диапазону изменений периода основного тона, указывает на характер возбуждения, а местоположение пика является хорошим индикатором периода основного тона (рис. 2.2).

Гомоморфные относительно свертки системы удовлетворяют обобщенному принципу суперпозиции. Принцип суперпозиции, если его записать для обычных линейных систем, имеет вид

 (2.1a)

 (2.1б)

где L – линейный оператор. Принцип суперпозиции устанавливает, что если сигнал на входе является линейной комбинацией элементарных сигналов, то и сигнал на выходе будет представлен в виде линейной комбинации соответствующих сигналов.

Прямым следствием принципа суперпозиции является тот факт, что сигнал на выходе линейной системы может быть представлен в виде дискретной свертки

 (2.2)

Символ « * » здесь и далее означает свертку в дискретном времени. По аналогии с принципом суперпозиции для обычных линейных систем определим класс систем, удовлетворяющих обобщенному принципу суперпозиции, в котором сложение заменяется сверткой (легко показать, что свертка обладает такими же алгебраическими свойствами, как и сложение [1]), т. е.

 (2.3)

В общем случае возможно сформулировать и уравнение, аналогичное (2.16), в котором выражено свойство скалярного умножения [2]. Системы, обладающие свойством (2.3), названы гомоморфными относительно свертки системами. Эта терминология объясняется тем [3], что данные преобразования оказываются гомоморфными преобразованиями линейного векторного пространства. При изображении таких систем операцию свертки представляют в явном виде на входе и выходе системы. Гомоморфный фильтр является гомоморфной системой, обладающей тем свойством, что одна компонента (выделяемая) проходит через эту систему без изменений, а другая – устраняется. В соотношении (2.3), например, если x₁(n) - нежелательная компонента, то необходимо потребовать, чтобы выход, соответствующий x₁(n), представлял собой единичный отсчет, в то время как выход, соответствующий х₂(n), близко совпадал бы с х₂(n). Это полностью аналогично ситуации в линейных системах, где ставится задача выделения сигнала из смеси его с аддитивным шумом.

Важным аспектом теории гомоморфных систем является то, что любая из них может быть представлена в виде каскадного соединения трех гомоморфных систем. Первый блок преобразует компоненты на входе, представленные в виде свертки, в аддитивную сумму на выходе. Второй блок -обычная линейная система, удовлетворяющая принципам суперпозиции в соответствии с (2.1). Третий блок является обратным первому, т. е. преобразует сигналы, представленные в виде суммы, в сигналы, представленные в виде свертки. Важность такого канонического представления заключается в том, что разработка гомоморфной системы сводится к разработке линейной системы. Блок*[], называемый характеристическим блоком гомоморфной относительно свертки системы, фиксирован при каноническом представлении. Очевидно, что обратное преобразование также фиксировано. Характеристическая система для гомоморфной обратной свертки подчиняется обобщенному принципу суперпозиции, в котором операция на входе – свертка, а на выходе – обычное сложение. Свойства характеристической системы определяются выражением

 (2.4)

Аналогично обратная характеристическая система удовлетворяет соотношению

(2.5)

Математическое описание характеристической системы определяется требованиями к выходному сигналу. Если на входе имеется сигнал свертки, то

 (2.6)

и z-преобразование входного сигнала имеет вид

 (2.7)

Из (2.4) очевидно, что z-преобразование сигнала на выходе системы должно представлять собой сумму z-преобразований компонент. Таким образом, в частотной области характеристическая система для свертки должна обладать следующим свойством: если на входе имеется произведение компонент, то на выходе должна возникнуть их сумма.

С учетом возможности вычисления комплексного логарифма, обратное преобразование комплексного логарифма преобразования Фурье входного сигнала, являющееся выходом характеристической системы для свертки, имеет вид

 (2.8)

Выход характеристической системы назван «комплексным кепстром» Термин «кепстр» используется для величины

 (2.9)

Все системы этого класса отличаются только линейной частью. Выбор линейной системы определяется свойствами входного сигнала.

Следовательно, для правильного построения линейной системы необходимо прежде всего определить вид и структуру сигнала на выходе характеристической системы, т. е. рассмотреть свойства комплексного кепстра для типичных входных сигналов.

Для определения свойств комплексного кепстра достаточно рассмотреть случай рационального z-преобразования. Наиболее общая форма преобразования имеет вид

 (2.10)

где модули величин а_к, b_k, c_k и d_k меньше единицы. Таким образом, сомножители (1-a_kz^-1) и (1-c_kz^-1) соответствуют нолям и полюсам внутри единичной окружности, a (1-b_kz) и (1-d_kz) - нолям и полюсам вне единичной окружности. Параметр z^r означает соответствующую задержку во временной области. Комплексный логарифм X(z) имеет вид

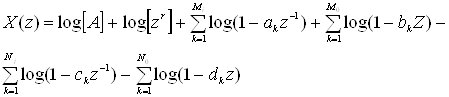. (2.11)

Когда (7.13) вычисляется на единичной окружности, легко видеть, что член  вносит вклад только в минимальную часть комплексного логарифма. Поскольку этот член несет информацию только о взаимном расположении во временной области, то при вычислении комплексного кепстра он обычно опускается [2]. Таким образом, при обсуждении свойств комплексного кепстра далее этот член не рассматривается. Используя то обстоятельство, что логарифм можно разложить в степенной ряд, относительно несложно показать, что комплексый кепстр имеет вид

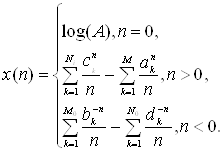 (2.12)

Уравнения (2.12) позволяют выявить ряд важных свойств комплексного кепстра. Прежде всего, комплексный кепстр в общем случае отличен от ноля и бесконечен как для положительных, так и для отрицательных значений n, даже если х(n) удовлетворяет принципу причинности, устойчив и имеет конечную протяженность. Далее видно, что комплексный кепстр является затухающей последовательностью, ограниченной сверху

 (2.13)

где α - максимальное абсолютное значение величин а,_k b_k, с_k и d_k, β -постоянный сомножитель.

Если Х(z) не содержит нулей и полюсов вне единичной окружности (т.е. b_k = d_k=0),то

 (2.14)

Такие сигналы называются минимально-фазовыми [1]. Общий результат для последовательности (2.14) состоит в том, что такая последовательность полностью определяется действительной частью преобразования Фурье. Таким образом, для минимально-фазовых систем комплексный кепстр определяется лишь логарифмом модуля преобразования Фурье. Это можно легко показать, если вспомнить, что действительная часть преобразования Фурье представляет собой преобразование Фурье от четной части последовательности, т. е. если  – преобразование Фурье кепстра, то

 (2.15)

Используя (2.14) и (2.15) легко показать, что

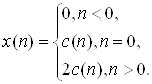(2.16)

Таким образом, для минимально-фазовых последовательностей комплексный кепстр можно получить путем вычисления кепстра и последующего использования (2.16). Другой важный результат для минимально-фазовых систем заключается в: том, что комплексный, кепстр можно вычислить рекуррентно по входному сигналу [1, 2, 5]. Рекуррентная формула имеет вид

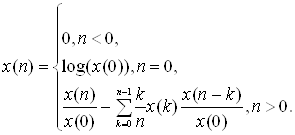 (2.17)

Аналогичные результаты можно получить и тогда, когда Х(г) не содержит полюсов и нулей, лежащих внутри единичной окружности. Такие сигналы называют максимально-фазовыми. Для этого случая, как это видно из (2.12),

 (2.18)

Совместное использование (2.14) и (2.15) даёт

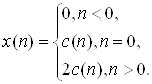(2.19)

Как и в случае минимально-фазовых последовательностей, здесь также можно получить рекуррентное соотношение для кепстра

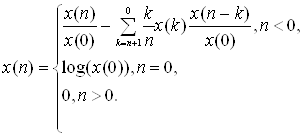 (2.20)

Похожие работы

Методика преподавания темы: Использование электронных таблиц для финансовых и других расчетов в 10 классе

Скачать

216371

14

6

... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...

Программирование и достижения компьютерной техники

Скачать

60551

0

0

... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники   1.         Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...

Методы позиционирования и сжатия звука

Скачать

461693

14

14

... информация должна поступать в декодер при восстановлении звукового сигнала. Декодер преобразует серию сжатых мгновенных спектров сигнала в обычную цифровую волновую форму. Audio MPEG - группа методов сжатия звука, стандартизованная MPEG (Moving Pictures Experts Group - экспертной группой по обработке движущихся изображений). Методы Audio MPEG существуют в виде нескольких типов - MPEG-1, MPEG-2 и ...

Использование высоких технологий криминальной средой. Борьба с преступлениями в сфере компьютерной информации

Скачать

430825

6

4

... с применением полиграфических компьютерных технологий? 10. Охарактеризуйте преступные деяния, предусмотренные главой 28 УК РФ «Преступления в сфере компьютерной информации». РАЗДЕЛ 2. БОРЬБА С ПРЕСТУПЛЕНИЯМИ В СФЕРЕ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ ГЛАВА 5. КОНТРОЛЬ НАД ПРЕСТУПНОСТЬЮВ СФЕРЕ ВЫСОКИХ ТЕХНОЛОГИЙ 5.1 Контроль над компьютерной преступностью в России Меры контроля над ...