Основы цифровой фильтрации

1.2  Основы цифровой фильтрации

Цифровой фильтр представляет собой систему с постоянными параметрами (инвариантную к сдвигу), работающую в дискретном времени. Напомним, что для таких систем сигнал на входе и выходе связан дискретной сверткой (1.5). Соответствующее соотношение между z-преобразованиями имеет вид

(1.37)

Прямое z-преобразование отклика на единичный импульс H(z) называется передаточной функцией системы. Преобразование Фурье отклика на единичный импульс называется частотной характеристикой. Обычно  представляет собой комплексную функцию со, которую можно записать в виде

(1.38)

или через модуль и фазу

(1.39)

Инвариантная к сдвигу линейная система называется физически реализуемой, если h(n)=0 при n<0. Линейная система устойчива, если для любой ограниченной по уровню входной последовательности выходная последовательность также ограничена. Необходимым и достаточным условием устойчивости линейной системы с постоянными параметрами является

(1.40)

Это условие аналогично (1.10) и оказывается достаточным для существования .

Сигналы на входе и выходе линейных инвариантных к сдвигу систем, таких, например, как фильтры, связаны дискретной сверткой (1.5) и кроме того, разностным уравнением

 (1.41)

Вычисляя z-преобразование от обеих частей, можно получить

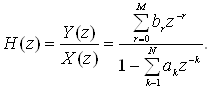 (1.42)

Сравнивая (1.41) и (1.42), полезно отметить следующее. Если задано разностное уравнение вида (1.41), то H(z) можно получить непосредственной подстановкой коэффициентов при входном сигнале в числитель передаточной функции к соответствующим степеням z^-1, а коэффициенты при выходном сигнале - в знаменатель к соответствующим степеням z^-1.

Передаточная функция в общем случае является дробно рациональной. Таким образом, она определяется положением нулей и полюсов на z-плоскости. Это означает, что H(z) можно представить в виде

 (1.43)

При рассмотрении z-преобразования отмечалось, что физически реализуемые системы имеют область сходимости вида |z|>R₁. Если система, кроме того, еще и устойчива, то R₁ должно быть меньше единицы, таким образом единичная окружность входит в область сходимости. Иначе говоря, для устойчивой системы все полюсы H(z) должны лежать внутри единичной окружности.

Достаточно определить два типа линейных систем с постоянными параметрами. Это системы с конечной импульсной характеристикой (КИХ) и системы с бесконечной импульсной характеристикой (БИХ). Эти два класса обладают отличными друг от друга свойствами, которые будут рассмотрены ниже.

Если все коэффициенты а_k. в уравнении (1.22) равны нулю, то разностное уравнение принимает вид

 (1.44)

Сравнивая (1.44) с (1.56), можно отметить, что

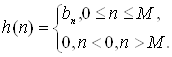 (1.45)

Системы с КИХ обладают рядом важных свойств. Передаточная функция H(z) таких систем представляет собой полином по степеням z^-1 и, таким образом, не имеет ненулевых полюсов, а содержит только нули. Системы с КИХ могут обладать строго линейной фазо-частотной характеристикой (ФЧХ). Если h(n) удовлетворяет условию

 (1.46)

то

 (1.47)

где  - действительная или чисто мнимая величина в зависимости от знака в (1.48).

Возможность получения строго линейной ФЧХ является очень важным обстоятельством применительно к речевым сигналам в тех случаях, когда требуется сохранить взаимное расположение элементов сигнала. Это свойство систем с КИХ существенно облегчает решение задачи их проектирования, поскольку все внимание можно уделять лишь аппроксимации амплитудно-частотной характеристики (АЧХ). За это достоинство фильтра с линейной ФЧХ, приходится расплачиваться необходимостью аппроксимации протяженной импульсной реакции в случае фильтров с крутыми АЧХ. Хорошо разработаны три метода проектирования КИХ-фильтров с линейными ФЧХ: взвешивания, частотной выборки и проектирования оптимальных фильтров с минимаксной ошибкой [1-3]. Второй и третий методы являются оптимизационными и используют итеративный (в отличие от замкнутой формы) подход для определения коэффициентов фильтра. Несмотря на простоту метода взвешивания, широкое применение нашли все три метода. Это обусловлено завершенностью глубоких исследований оптимальных КИХ-фильтров а, кроме того, наличием подробно описанных программ, позволяющих пользователю легко рассчитать любой фильтр [1,2,11].

При рассмотрении вопросов реализации цифровых фильтров полезно изображать их в виде схем. Разностное уравнение (1.25) изображено на рис. 1.4. Подобные схемы, называемые структурными, описывают в графической форме те операции, которые необходимо проделать над входной последовательностью для получения сигнала на выходе.

Для фильтра после подстановки (1.49) в(1.51) и выполнения интегрирования получается

 (1.52)

Импульсная характеристика (1.32) определена при любых целых значениях к и является бесконечной, поэтому ограничивают значения k. Пусть |k|≤К, где К=(N-1)/2 для фильтров с нечётными значениями N и К=N/2 для фильтров с чётными значениями N. Тогда конечная импульсная характеристика, соответствующая (1.52), записывается в виде

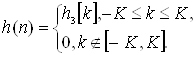 (1.53)

Импульсная характеристика (1.53) является некаузальной, так как имеет ненулевые значения при k<0. Чтоб получить каузальную характеристику, необходимо задержать  на К тактов, т.е.

 (1.54)

Синтезированный таким образом фильтр будет иметь значительные пульсации вблизи частоты среза. Указанные пульсации представляют эффект Гиббса, проявляющийся вблизи точек разрыва заданной частотной характеристики. Эффект Гиббса обусловлен ограничением длительности бесконечной импульсной характеристики .

Конечная импульсная характеристика , получаемая из , может быть также представлена в виде

 (1.55)

где w[k] - прямоугольное весовое окно длиной N отсчётов. Умножение заданной импульсной характеристики на прямоугольное окно приводит к искажению частотной характеристики синтезируемого фильтра. Частотная характеристика, соответствующая (1.55), будет равна свёртке заданной частотной характеристики прямоугольного окна. Таким образом, эффект Гиббса связан с пульсирующим поведением частотной характеристики прямоугольного весового окна.

Для уменьшения отрицательного влияния эффекта Гиббса применяют весовые окна, отличные от прямоугольного. Здесь имеет место аналогия со спектральным анализом, когда для уменьшения утечки энергии в боковые лепестки применяют оконные функции. С целью обеспечения линейности фильтра низких частот указанные оконные функции должны быть симметричными w[k]=w[N-k-1] и определены для значений k, лежащих диапазоне 0≤k≤N-1 [6].

Похожие работы

Методика преподавания темы: Использование электронных таблиц для финансовых и других расчетов в 10 классе

Скачать

216371

14

6

... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...

Программирование и достижения компьютерной техники

Скачать

60551

0

0

... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники   1.         Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...

Методы позиционирования и сжатия звука

Скачать

461693

14

14

... информация должна поступать в декодер при восстановлении звукового сигнала. Декодер преобразует серию сжатых мгновенных спектров сигнала в обычную цифровую волновую форму. Audio MPEG - группа методов сжатия звука, стандартизованная MPEG (Moving Pictures Experts Group - экспертной группой по обработке движущихся изображений). Методы Audio MPEG существуют в виде нескольких типов - MPEG-1, MPEG-2 и ...

Использование высоких технологий криминальной средой. Борьба с преступлениями в сфере компьютерной информации

Скачать

430825

6

4

... с применением полиграфических компьютерных технологий? 10. Охарактеризуйте преступные деяния, предусмотренные главой 28 УК РФ «Преступления в сфере компьютерной информации». РАЗДЕЛ 2. БОРЬБА С ПРЕСТУПЛЕНИЯМИ В СФЕРЕ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ ГЛАВА 5. КОНТРОЛЬ НАД ПРЕСТУПНОСТЬЮВ СФЕРЕ ВЫСОКИХ ТЕХНОЛОГИЙ 5.1 Контроль над компьютерной преступностью в России Меры контроля над ...