Кодирование речи на основе линейного предсказания

2.2 Кодирование речи на основе линейного предсказания

Линейное предсказание является одним из наиболее эффективных методов анализа речевого сигнала. Этот метод - доминирующий при оценке таких основных параметров речевого сигнала как период основного тона, форманты, спектр, функция площади речевого тракта, а также при сокращённом представлении речи с целью её низкоскоростной передачи и экономного хранения. Важность метода обусловлена высокой точностью получаемых оценок и относительной простотой вычислений.

Линейное предсказание - это метод анализа, основанный на цифровой фильтрации оцифрованной речи, при которой текущий отсчет сигнала может быть «предсказан» (например, при автоматическом синтезе речи) линейной комбинацией прошлых значений выходной последовательности и настоящих, а также прошлых значений входной последовательности. Понятие «линейная комбинация» означает сумму произведений известных дискретных отсчетов сигнала (входных и выходных), умноженных на соответствующие коэффициенты линейного предсказания для предсказания (определения) неизвестного выходного отсчета. При линейном предсказании основная задача анализа речи – найти коэффициенты этой линейной комбинации, которые дают минимальную ошибку предсказания на участке анализа сигнала.

Модель сигнала, наиболее часто используемая при линейном предсказании, сводится к получению неизвестного отсчета х(n) без учета предыдущих входных воздействий на выходе некоторой системы

 (2.21)

 (2.22)

где р – число коэффициентов, используемых в модели; k – коэффициенты линейного предсказания; G – коэффициент усиления, определяющий вклад в линейную комбинацию входного отсчета; u(n) – текущий входной отсчет.

Задача анализа оцифрованной речи сводится к определению коэффициентов k и G этой модели. Метод определения величин, используемых при расчетах, называется методом наименьших квадратов. Чтобы понять его суть, пойдем на некоторые упрощения в представлении текущего выходного отсчета. Будем считать, что входное воздействие на вход системы, моделирующей формирование речевых сигналов, ненаблюдаемо, что справедливо для ряда прикладных задач. Тогда на интервале анализа текущие отсчеты речевого сигнала приближенно опишутся линейной комбинацией предыдущих значений.

х(n) = а₁х(n -1) + а₂х(n - 2) +... + а_kх(n - k) +... + а_рх(n -р) = (2.23)

где х(n-1),...,х(n-р) - предыдущие значения речевого сигнала. Получаемая при этом ошибка предсказания ε_р называется иногда остатком предсказания и равняется

 (2.24)

Коэффициенты линейного предсказания а вычисляются из условия минимума среднеквадратичного значения ошибки на интервале анализа. На этом интервале полная среднеквадратичная ошибка складывается для каждого отсчета сигнала, представленного линейной комбинацией р предыдущих значений сигнала

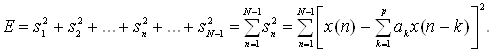 (2.25)

Здесь n – номер предыдущего отсчета сигнала на анализируемом интервале; k – номер предыдущего отсчета сигнала при построении линейной комбинации, представляющей текущий отсчет.

 (2.26)

Коэффициенты линейного предсказания, минимизирующие полную ошибку предсказания Е, находятся после того, как выражение для полной ошибки продифференцировать по всем коэффициентам (полная ошибка предсказания может рассматриваться как функция параметров а_k) и приравнять нулю все частные производные.

Частными производными называются производные сложной функции по одной из переменных с учетом того, что остальные переменные при таком дифференцировании считаются константами.

Результатом дифференцирования по а, является система из линейных уравнений с неизвестными коэффициентами линейного предсказания, минимизирующими ошибку линейного предсказания на отрезке анализа

сигнала, где коэффициенты k считаются постоянными.

Основной принцип метода линейного предсказания состоит в том, что текущий отсчет речевого сигнала можно аппроксимировать линейной комбинацией предшествующих отсчетов. Коэффициенты предсказания при этом определяются однозначно минимизацией среднего квадрата разности между отсчетами речевого сигнала и их предсказанными значениями (на конечном интервале). Коэффициенты предсказания – это весовые коэффициенты, используемые в линейной комбинации.

Основные положения метода линейного предсказания хорошо согласуются с моделью речеобразования, где показано, что речевой сигнал можно представить в виде сигнала на выходе линейной системы с переменными во времени параметрами, возбуждаемой квазипериодическими импульсами (в пределах вокализованного сегмента) или случайным шумом (на невокализованном сегменте). Метод линейного предсказания позволяет точно и надежно оценить параметры этой линейной системы с переменными коэффициентами.

Идеи и методы линейного предсказания довольно давно обсуждаются в технической литературе. Эти идеи используются в теориях автоматического управления и информации, где их называют методами оценивания систем, или металлами идентификации систем. Под термином «идентификация» понимаются методы линейного предсказания (ЛП), основанные на оценивании параметров, однозначно описывающих систему при условии, что ее передаточная функция является полюсной. Применительно к обработке речевых сигналов методы линейного предсказания означают ряд сходных формулировок задачи моделирования речевого сигнала [1,2]. Эти формулировки часто отличаются в исходных предпосылках. Иногда они сводятся, к различным методам вычисления, используемым для оценки коэффициентов предсказания. Так, применительно к речевым сигналам существуют следующие методы вычисления (часто равноценные); ковариационный [3], автокорреляционный [1, 2, 9], лестничного фильтра [11, 12].

обратной фильтрации [1], оценки спектра [12], максимального правдоподобия [4, 6] и скалярного произведения [1].

Целесообразность использования линейного предсказания обусловлена высокой точностью описания речевого сигнала с помощью модели.

Модель речеобразования в дискретном времени представляется в форме, наиболее удобной для решения задач линейного предсказания. В этом случае общий спектр, обусловленный излучением, речевым трактом и возбуждением, описывается с помощью линейной системы с переменными параметрами и передаточной функцией

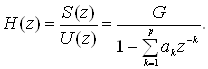 (2.27)

Эта система возбуждается импульсной последовательностью для вокализованных звуков речи и шумом для невокализованных. Таким образом, модель имеет, следующие параметры: классификатор вокализованных и невокализованных звуков, период основного тона для вокализованных сегментов, коэффициент усиления G и коэффициенты {а_k} цифрового фильтра. Все эти параметры, разумеется, медленно изменяются во времени.

Определение периода основного тона и классификация тон/шум могут быть осуществлены на основе использования ряда методов, в том числе с помощью рассматриваемых ниже методов линейного предсказания. Для вокализованных звуков хорошо подходит модель, содержащая только полюса в своей передаточной функции (чисто полюсная), но для носовых и фрикативных звуков требуется учитывать и нули. Если порядок р модели достаточно велик, то полюсная модель позволяет получить достаточно точное описание почти для всех звуков речи. Главное достоинство этой модели заключается в том, что как параметр G так и коэффициенты можно оценить непосредственно с использованием очень эффективных с вычислительной точки зрения алгоритмов.

Отсчет речевого сигнала s(n) связан е сигналом возбуждения u(n) простым разностным уравнением

 (2.28)

Линейный предсказатель с коэффициентами а_k определяется как система, на выходе которой имеем

 (2.29)

Системная функция предсказателя р-го порядка представляет собой полином вида

 (2.30)

Погрешность предсказания определяется как

 (2.31)

Из (2.31) видно, что погрешность предсказания представляет собой сигнал на выходе системы с передаточной функцией

 (2.32)

Сравнение (2.28) и (2.31) показывает, что если сигнал точно удовлетворяет модели (8.2), то e(n)=Gu(n). Таким образом, фильтр погрешности предсказания A (z) является обратным фильтром для системы H(z), соответствующей уравнению (2.27), т. е.

 (2.33)

Основная задача анализа на основе линейного предсказания заключается в непосредственном определении параметров {} по речевому сигналу с целью получения хороших оценок его спектральных свойств путем использования уравнения (2.31). Вследствие изменения свойств речевого сигнала во времени коэффициенты предсказания должны оцениваться на коротких сегментах речи. Основным подходом является определение параметров предсказания таким образом, чтобы минимизировать дисперсию погрешности на коротком сегменте сигнала. При этом предполагается, что полученные параметры являются параметрами системной функции H(z) в модели речеобразования.

То, что подобный подход приводит к полезным результатам, возможно, не сразу очевидно, но его полезность будет неоднократно подтверждена различными способами. Во-первых, пусть e(n)=Gu(n). Для вокализованной речи это означает, что е(n) будет состоять из последовательности импульсов, т.е. е(n) будет весьма мало почти все время. Поэтому в данном случае минимизация погрешности предсказания позволит получить требуемые коэффициенты. Другой повод, приводящий к тому же подходу, вытекает из того, что даже если сигнал формируется системой (2.28) с постоянными во* времени параметрами, которая возбуждается либо единичным импульсом, либо белым шумом, то можно показать, что коэффициенты предсказания, найденные по критерию минимизации среднего квадратического значения погрешности (в каждый момент времени), совпадают с коэффициентами в (2.28). Третьей, весьма важной для практики причиной является то, что подобная минимизация приводит к линейной системе уравнений, решение которых сравнительно легко приводит к получению параметров предсказания. Кроме того, полученные параметры, как это будет ясно из дальнейшего, составляют весьма плодотворную основу для точного описания сигнала. Кратковременная энергия погрешности предсказания

 (2.35)

 (2.36)

 (2.37)

где  - сегмент речевого сигнала, выбранный в окрестности отсчета n, т. е.

 (2.38)

Пределы суммирования справа в (2.35)-(2.37) пока не определены, но поскольку предполагается использовать концепции кратковременного анализа, то эти пределы всегда предполагаются конечными. Кроме того, для получения среднего значения необходимо разделить полученный результат на длину речевого сегмента, Однако эти константы несущественны с точки зрения решения системы линейных уравнений и поэтому далее опускаются. Параметры а_к можно получить, минимизируя Е_n в (2.37) путем вычисления, 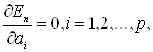что приводит к системе уравнений

 (2.38)

где - значения а_К, минимизирующие Е_n. Если ввести определение

 (2.39)

тогда (2.38) можно переписать в более компактном виде

 (2.40)

Эта система из р уравнений с р неизвестными может быть решена достаточно эффективным способом для получения неизвестных коэффициентов предсказания, минимизирующих средний квадрат погрешности предсказания на сегменте . Используя (2.37) и (2.39), можно показать, что средняя квадратическая погрешность предсказания имеет вид

 (2.41)

и, используя (2.40), можно выразить Е_n в виде

 (2.42)

Таким образом, общая погрешность предсказания состоит из двух слагаемых, одно из которых является постоянным, а другое - зависит от коэффициентов предсказания.

Для решения системы уравнений относительно коэффициентов предсказания следует первоначально вычислить величины , 1≤i≤р и 1≤o≤р. Только после этого можно переходить к решению (2.40) и получению оценок  Таким образом, принципиально анализ на основе линейного предсказания очень простой. Однако подробности, связанные с вычислением  и последующим решением системы уравнений, являются достаточно запутанными и нуждаются в дальнейшем обсуждении.

Хотя пределы суммирования в (2.35)-(2.37) и (2.39) не определены, в (2.39) они совпадают с соответствующими пределами в (2.35)-(2.37). Как было установлено, для кратковременного анализа соответствующие пределы должны охватывать конечный интервал. Имеется два подхода к этому вопросу, и в зависимости от пределов суммирования и выбора сегмента 8_п(ш) различают два метода линейного предсказания: автокорреляционный метод и ковариационный метод.

В зависимости от определения сегмента анализируемого сигнала можно получить две различные системы уравнений. Для автокорреляционного метода сигнал взвешивается с использованием N-точечного окна и величины  получаются на основе кратковременной автокорреляционной функции. Полученная матрица корреляций является теплицевой и приводит к первой системе уравнений для параметров предсказания. При ковариационном методе сигнал предполагается известным на множестве значений -p≤n≤N-1. Никаких предположений о сигнале вне данного интервала не делается, поскольку только этот интервал необходим для вычислений. Полученная матрица корреляций в данном случае симметричная, но не теплицева (симметричная и такая, что элементы на любой диагонали равны между собой). В результате два различных метода вычисления корреляции приводят к двум различным системам уравнений и к двум совокупностям коэффициентов предсказания с различными свойствами.

Похожие работы

Методика преподавания темы: Использование электронных таблиц для финансовых и других расчетов в 10 классе

Скачать

216371

14

6

... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...

Программирование и достижения компьютерной техники

Скачать

60551

0

0

... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники   1.         Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...

Методы позиционирования и сжатия звука

Скачать

461693

14

14

... информация должна поступать в декодер при восстановлении звукового сигнала. Декодер преобразует серию сжатых мгновенных спектров сигнала в обычную цифровую волновую форму. Audio MPEG - группа методов сжатия звука, стандартизованная MPEG (Moving Pictures Experts Group - экспертной группой по обработке движущихся изображений). Методы Audio MPEG существуют в виде нескольких типов - MPEG-1, MPEG-2 и ...

Использование высоких технологий криминальной средой. Борьба с преступлениями в сфере компьютерной информации

Скачать

430825

6

4

... с применением полиграфических компьютерных технологий? 10. Охарактеризуйте преступные деяния, предусмотренные главой 28 УК РФ «Преступления в сфере компьютерной информации». РАЗДЕЛ 2. БОРЬБА С ПРЕСТУПЛЕНИЯМИ В СФЕРЕ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ ГЛАВА 5. КОНТРОЛЬ НАД ПРЕСТУПНОСТЬЮВ СФЕРЕ ВЫСОКИХ ТЕХНОЛОГИЙ 5.1 Контроль над компьютерной преступностью в России Меры контроля над ...