Распространение звуков

1.3.3 Распространение звуков

Понятие звука почти совпадает с понятием колебаний. Звуковые волны возникают за счет колебаний. Они распространяются в воздухе или другой среде с помощью колебаний частиц этой среды. Следовательно, образование и распространение звуков в голосовом тракте подчиняется законам физики. В частности, основные законы сохранения массы, сохранения энергии, сохранения количества движения вместе с законами термодинамики и механики жидкостей применимы к сжимаемому воздушному потоку с низкой вязкостью, который является средой распространения звуков речи. Используя эти основные физические законы, можно составить систему дифференциальных уравнений в частных производных, описывающую движение воздуха в речеобразующей системе [1,2]. Составление и решение этих уравнений весьма затруднительны даже для простых предположений относительно формы голосового тракта и потерь энергии в речеобразующей системе. Полная акустическая теория должна учитывать следующие факторы:

-  изменение во времени формы голосового тракта;

-  потеря энергии на стенках голосового тракта за счет вязкого трения и теплопроводности;

-  мягкость стенок голосового тракта;

-  излучение звуковых волн через губы;

-  влияние носовой полости;

-  возбуждение голосового тракта.

Голосовой тракт можно представить в виде неоднородной трубы с переменной во времени площадью поперечного сечения. Для колебаний, длина волны которых превышает размеры голосового тракта (это обычно имеет место на частотах ниже 4000 Гц), можно допустить, что вдоль продольной оси трубы распространяется плоская волна. Дальнейшее упрощение состоит в предположении отсутствия потерь на вязкость и теплопроводность как внутри воздушного потока, так и на стенках трубы. На основе законов сохранения массы, количества движения и энергии с учетом перечисленных допущений Портнов показал, что звуковые волны, в трубе удовлетворяют следующим уравнениям

 (1.56а)

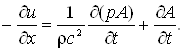 (1.56б)

где р=р(х,t) – звуковое давление как функция х и t; u=u(х,t) – скорость воздушного потока (volume velocity) как функция х и t, ρ - плотность воздуха в трубе; с - скорость распространения звука; A=A(x,t) - «функция площади», т. е. площадь поперечного сечения в направлении, перпендикулярном продольной оси трубы, как функция расстояния вдоль этой оси и времени. Сходная система уравнений была получена Сондхи,

Замкнутое решение уравнений (1.36) получить невозможно даже для простых форм трубы. Однако могут быть получены численные решения. Полное решение дифференциальных уравнений предполагает заданными давление и скорость потока для значений х и t в области голосовой щели и около губ, т. е. для получения решения должны быть заданы граничные условия у обоих концов трубы. Со стороны губ граничные условия должны отображать эффект излучения, а со стороны голосовой щели – характер возбуждения.

Кроме граничных условий необходимо задать функцию площади A(x,t). Для протяжных звуков можно предположить, что A(x,t) не изменяется во времени. Однако это предположение неверно для непротяжных звуков. Подробные измерения A(x,t) весьма затруднительны и могут быть выполнены только для протяжных звуков. Одним из методов проведения таких измерений является рентгеновская киносъемка. Фант и Перкелл провели несколько таких экспериментов. Однако подобные измерения могут быть выполнены лишь в ограниченном объеме. Другим методом является вычисление формы голосового тракта по акустическим измерениям. Описав подобный метод, предполагающий возбуждение голосового тракта внешним источником. Оба метода являются полезными для получения сведений о динамике речеобразования. Тем не менее, они не могут быть применены для получения описания речевых сигналов, например, в задачах связи. В работе Атала описаны результаты прямого измерения A(x,t) по сигналу речи, произнесенной в нормальных условиях.

Точное решение уравнений (1.36) является весьма сложным, даже если значение A(x,t) точно известно. Вместе с тем для решения поставленной задачи нет необходимости в точном и общем решениях этих уравнении [1,2].

1.4 Обработка речевого сигнала во временной области

В основе большинства методов обработки речи лежит предположение о том, что свойства речевого сигнала с течением времени медленно изменяются; Это предположение приводит к методам кратковременного анализа, в которых сегменты речевого сигнала выделяются и обрабатываются так, как если бы они были короткими участками отдельных звуков с отличающимися свойствами. Процедура повторяется так часто, как это требуется. Сегменты, которые иногда называют интервалами, (кадрами) анализа обычно пересекаются. Результатом обработки на каждом интервале является число или совокупность чисел. Следовательно, подобная обработка приводит к новой, зависящей от времени последовательности, которая.может служить характеристикой речевого сигнала.

Большинство методов кратковременного анализа, в том числе и кратковременный Фурье-анализ, могут быть описаны выражением

 (1.57)

Речевой сигнал (возможно, после ограничения частотного диапазона в линейном фильтре) подвергается преобразованию Т[·], линейному или нелинейному, которое может зависеть от некоторого управляющего параметра или их совокупности. Результирующая последовательность умножается затем на последовательность значений временного окна (весовой функции), расположенную во времени в соответствии с индексом п. Результаты затем суммируются по всем ненулевым значениям. Обычно, хотя и не всегда, последовательность значений временного окна имеет конечную протяженность. Значение Q_n представляет собой, таким образом, «взвешенное» среднее значение последовательности Т [х (m)].

Простым примером, иллюстрирующим изложенное, может служить измерение кратковременной энергии сигнала. Полная энергия сигнала в дискретном времени определяется как

 (1.58)

Вычисление этой величины не имеет особого смысла при обработке речевых сигналов, поскольку она не содержит информации о свойствах сигнала, изменяющихся во времени. Кратковременная энергия определяется выражением

 (1.59)

Таким образом, кратковременная энергия в момент n есть просто сумма квадратов N отсчетов от n-N-1 до n. Из (1.37) видно, что в (1.39) Т [•] есть просто операция возведения в квадрат, а

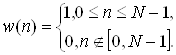 (1.60)

Вычисление кратковременной энергии, иллюстрирует рис. 1.6 Окно «скользит» вдоль последовательности квадратов значений сигнала, в общем случае вдоль последовательности Т[х(m)], ограничивая длительность интервала, используемого в вычислениях.

Как отмечалось выше, амплитуда речевого сигнала существенно изменяется во времени.

В частности, амплитуда невокализованных сегментов речевого сигнала значительно меньше амплитуды вокализованных сегментов. Подобные изменения амплитуды хорошо описываются с помощью функции кратковременной энергии сигнала. В общем случае определить функцию энергий можно как

 (1.61)

Это выражение может быть переписано в виде

 (1.62)

где

 (1.63)

Сигнал х²(n) в этом случае фильтруется с помощью линейной системы с импульсной характеристикой h(n).

Выбор импульсной характеристики h(n) или окна составляет основу описания сигнала с помощью функции энергии. Чтобы понять, как влияет выбор окна на функцию кратковременной энергии сигнала, предположим, что h(n) в (1.35) является достаточно длительной и имеет постоянную амплитуду; значение Е_n будет при этом изменяться во времени незначительно. Такое окно эквивалентно фильтру нижних частот с узкой полосой пропускания. Полоса фильтра нижних частот не должна быть столь узкой, чтобы выходной сигнал оказался постоянным, иначе говоря, полосу следует выбрать так, чтобы функция энергии отражала изменения амплитуды речевого сигнала.

Описанная ситуация выражает противоречие, которое нередко возникает при изучении кратковременных характеристик речевых сигналов. Суть его состоит в том, что для описания быстрых изменений амплитуды желательно иметь узкое окно (короткую импульсную характеристику), однако слишком малая ширина окна может привести к недостаточному усреднению и, следовательно, к недостаточному сглаживанию функций энергии.

Влияние вида окна на вычисление изменяющейся во времени энергии сигнала можно проиллюстрировать на примере использования двух наиболее распространенных окон: прямоугольного и окна Хэмминга.

Прямоугольное окно, как это видно из (1.39), соответствует случаю, когда всем отсчетам на интервале от (n-N-1) до п приписывается одинаковый вес. Частотная характеристика прямоугольного окна равна

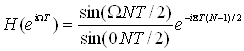 (1.64)

Для окна с шириной 51 отсчет (N=51) логарифм амплитудно-частотной характеристики представлен на рис. 1.6а.

Первое нулевое значение амплитудно-частотной характеристики (1.64) соответствует частоте

 (1.65)

где  частота дискретизации. Это номинальная частота среза фильтра нижних частот, соответствующего прямоугольному окну.

Амплитудно-частотная характеристика окна Хемминга при N=51 показана на рис. 1.6б. Полоса пропускания фильтра с окном Хемминга при одинаковой ширине примерно вдвое превосходит полосу фильтра с прямоугольным окном. Очевидно также, что окно Хемминга обеспечивает большее затухание вне полосы пропускания по сравнению с прямоугольным окном. Затухание, вносимое вне полосы, несущественно зависит от ширины каждого из окон. Это означает, что увеличение ширины приведет просто к сужению полосы. Если N мало (порядка периода основного тона или менее), то Е_n будет изменяться очень быстро, в соответствии с тонкой структурой речевого колебания. Если N велико (порядка нескольких периодов основного тона), то Е_n будет изменяться медленно и не будет адекватно описывать изменяющиеся особенности речевого сигнала. Это, к сожалению, означает, что не существует единственного значения М, которое в полной мере удовлетворяло бы перечисленным требованиям, так как период основного тона изменяется от 10 отсчетов (при частоте дискретизации 10 кГц) для высоких женских и детских голосов до 250 отсчетов для очень низких мужских голосов. На практике N выбирают равным 100—200 отсчетов при частоте дискретизации 10 кГц (т. е. длительность порядка 10-20 мс).

Основное назначение Е_n состоит в том, что эта величина позволяет отличить вокализованные речевые сегменты от невокализованных. Значения Е_n для невокализованных сегментов значительно меньше, чем для вокализованных. Функция кратковременной энергии может быть использована для приближенного определения момента перехода от вокализованного сегмента к невокализованному и наоборот, а в случае высококачественного речевого сигнала (с большим отношением сигнала к шуму) функцию энергии можно использовать и для отделения речи от пауз.

Одним из недостатков функции кратковременной энергии, определяемой выражением (1.35), является ее чувствительность к большим уровням сигнала (поскольку в (1.35) каждый отсчет возводится в квадрат). Вследствие этого значительно искажается соотношение между значениями последовательности х(n). Простым способом устранения этого недостатка является переход к определению функции среднего значения в виде

 (1.66)

где вместо суммы квадратов вычисляется взвешенная сумма абсолютных значений. Исключение операции возведения в квадрат упрощает арифметические вычисления.

При вычислении среднего значения по (1.46) динамический диапазон (отношение максимального значения к минимальному) определяется примерно как квадратный корень из динамического диапазона при обычном вычислении энергии. В данном случае различия в уровнях между вокализованной и невокализованной речью выражены не столь ярко, как при использовании функций энергии.

Поскольку полоса частот при определении как функции энергии, так и среднего значения приближенно совпадает с полосой пропускания используемого фильтра нижних частот, то нет необходимости дискретизировать эти функции столь же часто, как исходный речевой сигнал. Например, для окна длительностью 20 мс достаточна частота дискретизации около 100 Гц. Это означает, что значительная часть информации теряется при использовании подобных кратковременных представлений. Очевидно также, что информация, относящаяся к динамике амплитуд речевого сигнала, сохраняется в весьма удобной форме [1,2].

При обработке сигналов в дискретном времени считают, что если два последовательных отсчёта имеют различные знаки, то произошёл переход через ноль. Частота появления нолей в сигнале может служить простейшей характеристикой его спектральных свойств. Это наиболее справедливо для узкополосных сигналов.

Среднее число нулевых переходов можно принять в качестве подходящей оценки частоты синусоидального колебания.

Речевой сигнал является широкополосным и, следовательно, интерпретация среднего числа переходов через нуль менее очевидна. Однако можно получить грубые оценки спектральных свойств сигнала, основанные на использовании функции среднего числа переходов через нуль для речевого сигнала; рассмотрим способ вычисления этой величины. Функция среднего числа переходов через нуль имеет те же общие свойства, что и функции энергии и среднего значения. Все, что в действительности требуется, это проверить пары отсчетов с целью определения нулевых пересечений, а затем вычислить среднее по всем N последовательным отсчетам (деление на N, конечно, необязательно). Как и ранее, может быть вычислено взвешенное среднее и при использовании симметричных окон конечной длительности задержка может быть скомпенсирована точно. Могут быть получены и рекуррентные уравнения.

Рассмотрим теперь применение функции среднего числа переходов через нуль для обработки речевых сигналов. Модель речеобразоаания предполагает, что энергия вокализованных сегментов речевого сигнала концентрируется на частотах ниже 3 кГц, что обусловлено убывающим спектром сигнала возбуждения, тогда как, для невокализованных сегментов большая часть энергии лежит в области высоких частот. Поскольку высокие частоты приводят к большому числу переходов через нуль, а низкие – к малому, то существует жесткая связь между числом нулевых пересечений и распределением энергии по частотам. Разумно предположить, что большому числу нулевых пересечений соответствуют невокализованные сегменты, а малому числу — вокализованные сегменты речи. Это, однако, очень расплывчатое утверждение, поскольку мы не определили, что означает «много» или «мало», и количественно определить эти понятия в действительности трудно. Гауссовская кривая хорошо согласуется с приведенными гистограммами. Среднее число пересечений составляет 49 для вокализованных и 14 для невокализованных сегментов длительностью 10 мс.

Поскольку оба распределения перекрываются, нельзя вынести однозначное решение о принадлежности сегмента к вокализованным или невокализованным отрезкам только по среднему числу переходов через нуль. Тем не менее, подобное представление весьма полезно при осуществлении такой классификации.

Так же, как и в случае функций энергии и среднего, функцию среднего числа переходов через нуль можно дискретизировать с очень низкой частотой. Хотя среднее число переходов через нуль изменяется значительно, вокализованные и невокализованные сегменты просматриваются очень четко.

При использовании описания сигнала средним числом переходов через нуль следует иметь в виду ряд практических соображений. Хотя в основу алгоритма вычисления нулевых переходов положено сравнение знаков соседних отсчетов, тем не менее, при дискретизации сигнала следует предпринимать специальные меры.

Очевидно, что число нулевых переходов зависит от уровня шума при аналого-цифровом преобразовании, интенсивности фона переменного тока и других шумов, которые могут присутствовать в цифровой системе. Таким образом, с целью уменьшения влияния этих факторов следует проявлять особую осторожность при аналоговой обработке сигнала, предшествующей дискретизации. Например, часто оказывается более целесообразным использовать полосовой фильтр вместо фильтра нижних частот для уменьшения эффекта наложения при аналого-цифровом преобразовании и устранения фона переменного тока из сигнала. Кроме того, при измерении числа переходов через нуль следует учитывать соотношение между периодом дискретизации и интервалом усреднения N. Период дискретизации определяет точность выделения нулевых пересечений по времени (и по частоте), т. е. чтобы добиться высокой точности, нужна большая частота дискретизации. Вместе с тем от каждого отсчета требуется информация объемом лишь 1 бит (информация только о знаке сигнала).

Вследствие практической ограниченности этого метода было предложено множество сходных представлений сигнала. В каждом из них содержатся дополнительные особенности, направленные на снижение чувствительности оценок к шуму, но все они имеют и свои собственные ограничения. Наиболее заметным среди них является представление сигнала, исследованное Бейкером. Представление основано на интервалах времени между положительными переходами через нуль (снизу вверх). Бейкер применил это описание для фонетической классификации звуков речи.

Другое применение анализа переходов через нуль состоит в получении промежуточного представления речевого сигнала в частотной области. Метод включает фильтрацию речевого сигнала в нескольких смежных частотных диапазонах. Затем по сигналам на выходе фильтров измеряют кратковременную энергию и среднее число переходов через нуль. Совместное использование этих характеристик дает грубое описание спектральных свойств сигнала. Этот подход, предложенный Рэдди и исследованный Вайсенсом и Эрманом, положен в основу систем распознавания речи.

Задача определения моментов начала и окончания фразы при наличии шума является одной из важных задач в области обработки речи. В частности, при автоматическом распознавании слов важно точно определить моменты начала и окончания слова. Методы обнаружения моментов начала и окончания фразы можно использовать для уменьшения числа арифметических операций, если обрабатывать только те сегменты, в которых имеется речевой сигнал, например, в системах, работающих не в реальном масштабе времени.

Проблема отделения речи от окружающего шума очень сложна, за исключением случаев очень большого отношения сигнал/шум, т. е. в случае высококачественных записей, выполненных в заглушённой камере или звуконепроницаемой комнате. В этих случаях энергия даже наиболее слабых звуков речи (фрикативных согласных) превышает энергию шума и, таким образом, достаточно лишь измерить энергию сигнала. Но подобные условия записи, как правило, не встречаются в реальных ситуациях.

Похожие работы

Методика преподавания темы: Использование электронных таблиц для финансовых и других расчетов в 10 классе

Скачать

216371

14

6

... и менеджмента Санкт-Петербургского Государственного технического университета соответствовал поставленной цели. Его результаты позволили автору разработать оптимальную методику преподавания темы: «Использование электронных таблиц для финансовых и других расчетов». Выполненная Соловьевым Е.А. дипломная работа, в частности разработанная теоретическая часть и план-конспект урока представляет ...

Программирование и достижения компьютерной техники

Скачать

60551

0

0

... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники   1.         Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...

Методы позиционирования и сжатия звука

Скачать

461693

14

14

... информация должна поступать в декодер при восстановлении звукового сигнала. Декодер преобразует серию сжатых мгновенных спектров сигнала в обычную цифровую волновую форму. Audio MPEG - группа методов сжатия звука, стандартизованная MPEG (Moving Pictures Experts Group - экспертной группой по обработке движущихся изображений). Методы Audio MPEG существуют в виде нескольких типов - MPEG-1, MPEG-2 и ...

Использование высоких технологий криминальной средой. Борьба с преступлениями в сфере компьютерной информации

Скачать

430825

6

4

... с применением полиграфических компьютерных технологий? 10. Охарактеризуйте преступные деяния, предусмотренные главой 28 УК РФ «Преступления в сфере компьютерной информации». РАЗДЕЛ 2. БОРЬБА С ПРЕСТУПЛЕНИЯМИ В СФЕРЕ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ ГЛАВА 5. КОНТРОЛЬ НАД ПРЕСТУПНОСТЬЮВ СФЕРЕ ВЫСОКИХ ТЕХНОЛОГИЙ 5.1 Контроль над компьютерной преступностью в России Меры контроля над ...