Методы решения УУР

2.2 Методы решения УУР

В применяемом при расчетах установившихся режимов ШРЭС программно-вычислительном комплексе "RASTR" для решения УУР используется комбинация двух методов: метода Зейделя и метода Ньютона. При этом метод Зейделя используется в качестве стартового алгоритма (для оценки начальных приближений), а основным методом является классический метод Ньютона.

Метод Зейделя представляет собой незначительную модификацию метода простой итерации. Итерационное выражение метода простой итерации в матричном виде:

.

Элементы матрицы В – безразмерные величины вида 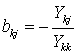, k≠j , а элементы вектора b имеют размерность напряжений, 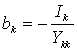, k, j=1, 2, 3.

Основная идея метода Зейделя в отличие от простой итерации заключается в том, что найденное (i+1)-е приближение (k-1)-го напряжения U⁽ⁱ⁺¹⁾_(k-1) сразу же используется для вычисления следующего, k-го напряжения U⁽ⁱ⁺¹⁾_k . Иными словами, полученное (i+1)-е значение напряжения сразу же используется для вычисления (i+1)-го значения напряжений U₂, U₃ и т. д.

По методу простой итерации (i+1)-е приближение k-го напряжения U⁽ⁱ⁺¹⁾_k для системы n-го порядка вычисляется по следующему выражению:

.

По методу Зейделя (i+1)-е приближение k-го напряжения U⁽ⁱ⁺¹⁾_k вычисляется так:

.

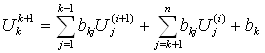Как правило, метод Зейделя надежнее и быстрее сходится, чем метод простой итерации. Кроме того, метод Зейделя требует несколько меньшей памяти, чем простая итерация, так как необходимо помнить только один вектор переменных. При решении по Зейделю, уравнений узловых напряжений сразу после вычисления (i+1)-е приближение (k)-го напряжения U⁽ⁱ⁺¹⁾_(k) записывается в ту же ячейку памяти, где ранее хранилось (i)-е приближение U⁽ⁱ⁾_(k). При использовании простой итерации необходимо помнить два вектора узловых напряжений, с ответствующих (i)-му и (i+1)-му шагам /6/.

Алгоритмическая реализация метода Зейделя столь же проста, как и простой итерации. Единственное изменение в алгоритме расчета состоит в засылке вычисленного U⁽ⁱ⁺¹⁾_(k), в то же место памяти, где ранее хранилось U⁽ⁱ⁾_(k). Поскольку метод простой итерации не имеет никаких преимуществ перед методом Зейделя, при практических расчетах установившихся режимов электрических систем на ЭВМ всегда используется метод Зейделя, а не простая итерация.

Если метод Зейделя сходится быстро и для решения системы n-го порядка требуется менее n шагов, то при расчете на ЭВМ получим выигрыш во времени в сравнении с точными методами, например с методом Гаусса. Это вытекает из того, что число арифметических операций, необходимых для одного шага метода Зейделя, пропорционально n², а общее число арифметических операций, например в методе Гаусса, пропорционально n³. Приведенное соотношение числа операций справедливо для расчетов установившегося режима, если не учитывается слабая заполненность матриц узловых проводимостей. В то же время и в случае учета слабой заполненности этих матриц метод Зейделя, если он сходится быстро, требует меньше времени ЭВМ, чем точные методы. Отдельное достоинство этого метода заключается в быстром приближении к области решения в течении нескольких начальных итераций, поэтому он и используется в качестве стартового в ПВК "Rastr". В дальнейшем сходимость метода замедляется, поэтому он и не получил широкого применения в качестве основного метода расчета.

Другое важное достоинство метода Зейделя состоит в простоте алгоритма и в удобстве его реализации на ЭВМ. Он особенно эффективен при учете слабой заполненности матрицы узловых проводимостей, поскольку алгоритм такого учета в методике Зейделя весьма прост. В результате экономия памяти при использовании метода Зейделя становится тем существенней, чем больше узлов содержит электрическая система. Применение специальных методов учета слабой заполненности при применении точных методов несколько уменьшает преимущество метода Зейделя с точки зрения необходимого объема памяти ЭВМ. Однако в точных методах такой учет алгоритмически сложен и даже при его применении метод Зейделя все равно требует меньше памяти ЭВМ.

Существенный недостаток метода Зейделя - его медленная сходимость или даже расходимость при расчете электрических систем с устройствами продольной компенсации, с трехобмоточньтми трансформаторами, когда сопротивление обмотки среднего напряжения очень мало, а так же при расчетах предельных и неустойчивых режимов.

Метод Ньютона пригоден для решения обширного класса нелинейных уравнений. Идея метода Ньютона состоит в последовательной замене на каждой итерации системы нелинейных уравнений некоторой линейной системой, решение которой дает значения неизвестных, более близких к решению нелинейной системы, чем исходное приближение. Решая линейное уравнение определяем поправку Δx⁽¹⁾ к начальному приближению:

Δx⁽¹⁾= x⁽¹⁾- x⁽⁰⁾.

За новое приближение неизвестного принимаем:

x⁽¹⁾= x⁽⁰⁾+ Δx⁽¹⁾.

Аналогично определяем следующие приближения:

x⁽ⁱ⁺¹⁾= x⁽ⁱ⁾+ Δx⁽ⁱ⁺¹⁾.

Итерационный процесс сходится если функция невязок будет близка к нулю. Сходимость считается достигнутой, если абсолютная величина невязки меньше заданной, т. е. при

.

Уравнение узловых напряжений в форме баланса мощностей для k-го узла записывается в виде:

.

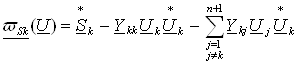В этом выражении для удобства записи слагаемое  внесено в сумму, причем балансирующему узлу присвоен номер n+1. Для того, чтобы оперировать с вещественными величинами, выделяют действительные и мнимые части в этом уравнении. В качестве неизвестных при решении уравнений установившегося режима используются модули и фазы напряжений в узлах. Уравнения баланса мощностей при таких переменных можно получить в следующем виде:

;

;

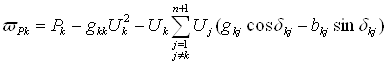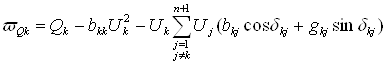где δ_kj=δ_k- δ_j ; k = 1,…,n.

В этом случае

,

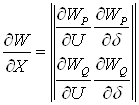элементы матрицы Якоби – это частные производные небалансов активной и реактивной мощностей по модулям и фазам напряжений узлов. Если активные и реактивные мощности заданы во всех узлах, то число уравнений узловых напряжений баланса мощности и число переменных равно 2n.

Метод Ньютона широко применяется для расчетов установившихся режимов на ЭВМ. Он не мог претендовать на практические применения в задачах расчета сетей до использования ЭВМ из-за трудоемкости вычисления матрицы производных. Широкое применение для расчетов установившихся режимов на ЭВМ метод Ньютона получил с 60-х годов /6/.

Матрица Якоби системы уравнений установившегося режима слабо заполнена, как и матрица Y_у. Поэтому в расчетах режимов на ЭВМ на каждом шаге метода Ньютона можно использовать способы учета слабой заполненности. Важнейшие преимущества метода Ньютона в расчетах установившихся режимов на ЭВМ – быстрая квадратичная сходимость и возможность учета слабой заполненности матрицы производных. Метод Ньютона можно успешно применять для расчетов установившихся режимов при их комплексной оптимизации.

Метод Ньютона требует столько же памяти ЭВМ, сколько при решении на каждом шаге линейных уравнений узловых напряжений по Гауссу, т. е. больше, чем по методу Зейделя но значительно меньше, чем при использований матрицы Z_у. Для увеличения скорости и надежности расчета установившегося режима применяются различные модификации метода Ньютона.

По окончании расчета установившегося режима можно приступать к его оптимизации.