Навигация
Общая характеристика и математическая постановка задачи оптимизации электрических режимов
2.3 Общая характеристика и математическая постановка задачи оптимизации электрических режимов
При передаче электрической энергии от шин электростанций до потребителей часть электроэнергии неизбежно расходуется на нагрев проводников, создание электромагнитных полей и прочие эффекты. При анализе потерь электроэнергии принято различать следующие виды потерь:
- отчетная величина потерь электроэнергии в энергосистеме – определяемая как разность между количеством электроэнергии, отпущенной в сеть собственными электростанциями, электростанциями других ведомств и соседними энергопредприятиями, и реализованной электроэнергией, вычисленной по сумме оплаченных счетов от потребителей;
- расчетная или техническая величина потерь, определяемая по известным параметрам режимов работы и параметрам элементов сети, она обусловлена расходом электроэнергии на нагрев проводников и создание электромагнитных полей;
- коммерческие потери – определяемые как разность между отчетными и техническими потерями, они обусловлены несовершенством системы учета, неодновременностью и неточностью снятия показаний счетчиков, погрешностью используемых приборов учета, неравномерностью оплаты электропотребления, наличием безучетных потребителей, хищениями и т. д.
Оптимизация режимов работы ВЭС в данной работе будет нацелена на снижение именно технической величины потерь электроэнергии.
Оптимизация режима по напряжению, реактивной мощности и коэффициентам трансформации является частью комплексной задачи оптимизации режима "по всем переменным", т. е. задачи экономического распределения активных и реактивных мощностей с учетом ограничений по надежности и качеству энергии. Однако влияние основных переменных – активных мощностей электростанций – на распределение реактивных мощностей весьма значительно, а обратное влияние относительно невелико. Этим оправдывается практическое решение задачи оптимизации режима по напряжению, реактивной мощности и коэффициентам трансформации как задачи "дооптимизации" режима при заданном распределении активных мощностей.
Практически решение задачи оптимизации режима энергосистем по напряжению и реактивной мощности сводится к следующему. Для центров питания с возможностью независимого регулирования напряжения (в пределах, ограниченных располагаемыми техническими средствами) устанавливаются графики желательных и предельно допустимых уровней напряжения (таблица 1.2), и эти центры служат контрольными точками по режиму напряжения. Кроме того, выбираются контрольные точки по напряжению в узлах основной сети, поддержанием заданного графика в которых обеспечиваются требуемые уровни напряжения в центрах питания, не имеющих собственных (местных) средств регулирования напряжения.
Отметим, что полученное значение потерь электроэнергии после реализации всех рекомендаций в общем случае будет отличаться на величину коммерческих потерь и некоторого значения (не обязательно положительного), обусловленного не учетом влияния погодных условий.
Таблица 2.1 – Графики желательных и предельно допустимых напряжений в киловольтах
| Режим | Класс напряжения, кВ |
|
|
| 1 | 6 |
|
|
| 10 |
|
| |
| 35 |
|
| |
| 110 |
|
| |
| 220 |
|
| |
| 500 |
|
| |
| 2, 3, 4 | 6 |
|
|
| 10 |
|
| |
| 35 |
|
| |
| 110 |
|
| |
| 220 |
|
| |
| 500 |
|
|
Поясним на примере обозначенную выше взаимосвязь между потерями мощности и значениями напряжения в узлах, реактивной мощности источников и коэффициентов трансформации. Рассмотрим фрагмент сети, схема замещения которого в общем случае содержит следующие комплексные параметры (рис. 2): продольное сопротивление ![]() (проводимость
(проводимость  ) с нагрузочными потерями при протекании тока нагрузки
) с нагрузочными потерями при протекании тока нагрузки ![]() по линиям и трансформаторам и поперечную проводимость (шунт проводимости)
по линиям и трансформаторам и поперечную проводимость (шунт проводимости) ![]() , отражающую преимущественно потери холостого хода трансформаторов, компенсирующих устройств и линий. В схеме замещения учтен идеальный трансформатор с действительным оэффициентом трансформации
, отражающую преимущественно потери холостого хода трансформаторов, компенсирующих устройств и линий. В схеме замещения учтен идеальный трансформатор с действительным оэффициентом трансформации ![]() (
(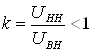 ), поскольку в данных сетях производится только продольное регулирование напряжения и перераспределение реактивной мощности. Комплексные значения напряжения в начале участка
), поскольку в данных сетях производится только продольное регулирование напряжения и перераспределение реактивной мощности. Комплексные значения напряжения в начале участка ![]() и в его конце
и в его конце ![]() , различается падением напряжения
, различается падением напряжения ![]() и объединенные трансформацией в виде
и объединенные трансформацией в виде
![]() ,
,
определяются из расчетов исходного и оптимального режимов. В электрических сетях 35-110 кВ потери напряжения в основном определяются продольной составляющей падения напряжения
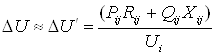 ,
,
величина которой, а следовательно и значения напряжений в узлах в силу соотношения ![]() преимущественно определяется потоками реактивной мощности.
преимущественно определяется потоками реактивной мощности.
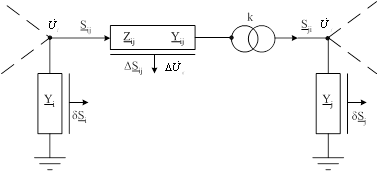
Рисунок 2 – Общий фрагмент схемы замещения электрической сети
Взаимосвязь параметров данной оптимизационной задачи можно представить с помощью известных формул. Потери активной мощности
![]() ,
, 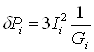 ,
,
зависят от величины тока в продольной части схемы замещения (рис. 2)
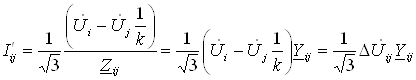 ,
,
и в ее поперечной части
![]() .
.
Анализируемые потери мощности выразим через модули напряжений и потери напряжения: в продольной части схемы замещения в виде
 ,
,
или иначе ![]() ,
,
а также в виде
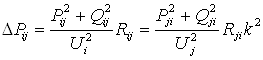 ;
;
в поперечной части
![]() ,
, ![]() .
.
Отметим также зависимость потоков активной и реактивной мощностей
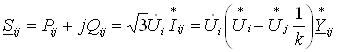 ,
,
![]() ,
,
и зарядной (емкостной) мощности шунтов
![]() ,
, ![]() ,
,
от оптимизируемых значений напряжений и трансформаций.
В итоге для электрической сети с n узлами суммарные потери мощности предстают в виде
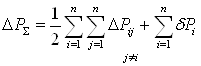 ,
,
Точное суммирование (интегрирование) потерь мощности в сети с m – ветвями и n – узлами при неизменном в период времени ![]() составе и схеме позволяет определить суммарные потери электроэнергии в виде
составе и схеме позволяет определить суммарные потери электроэнергии в виде
![]() .
.
Из выражений (2.22) следует, что для снижения нагрузочных потерь необходимо увеличить напряжение в узлах сети и в целом уровень (среднее значение) напряжения в ней. В то же время для снижения потерь холостого хода (2.23) уровень напряжения необходимо снижать. Воздействовать на напряжения и нагрузочные потери согласно выражениям (2.15), (2.16), (2.17) можно также путем снижения реактивных нагрузок продольных элементов сети, что достигается компенсацией реактивных нагрузок потребителей либо более благоприятным перераспределением перетоков ![]() реактивной мощности в ветвях замкнутой сети /4, 7, 8/. Оба указанных мероприятия могут быть реализованы в ПЭС с помощью местных источников реактивной мощности, регулируемых трансформаторов в замкнутых контурах и оптимальным размыканием контуров. Поскольку потери мощности зависят от режима напряжений (2.20) - (2.23), а последний тесно связан с распределением реактивной мощности и трансформациями в сетях (2.15), (2.26), (2.27), понятие регулирования напряжения, реактивной мощности и коэффициентов трансформации объединяют, а соответствующую задачу решают совместно /9, 10/.
реактивной мощности в ветвях замкнутой сети /4, 7, 8/. Оба указанных мероприятия могут быть реализованы в ПЭС с помощью местных источников реактивной мощности, регулируемых трансформаторов в замкнутых контурах и оптимальным размыканием контуров. Поскольку потери мощности зависят от режима напряжений (2.20) - (2.23), а последний тесно связан с распределением реактивной мощности и трансформациями в сетях (2.15), (2.26), (2.27), понятие регулирования напряжения, реактивной мощности и коэффициентов трансформации объединяют, а соответствующую задачу решают совместно /9, 10/.
Таким образом анализ составляющих потерь (2.20), (2.21), (2.22) в составе выражения их суммарных значений (2.26), (2.27), показывает, что экономичность режимов работы сетей в значительной мере зависит от сочетания коэффициентов трансформации и реактивных мощностей источников, влияющих на напряжения узлов, правильный выбор которых позволяет улучшить режим напряжений узлов и снизить потери мощности и энергии.
В итоге возникает оптимизационная задача определения таких взаимосвязанных напряжений, коэффициентов трансформации и реактивных мощностей источников, при реализации которых суммарные потери активной мощности или электроэнергии сети (2.26) будут минимальны.
При этом задача оптимизации режимов ЭС, относится к классической задаче нелинейного математического программирования, в общем случае имеет следующую формулировку /11, 12/: для (n+1) узлов ЭЭС найти минимум целевой функции
![]() ,
,
соответствующей функции суммарных потерь активной мощности (2.26) или ЭЭ (2.27) при условии баланса мощностей в узлах
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
и при выполнении эксплуатационных и технических ограничений в виде неравенств
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Предусмотрено разделение переменных ![]() на зависимые (базисные)
на зависимые (базисные) ![]() и независимые (регулируемые)
и независимые (регулируемые) ![]() переменные.
переменные.
Ограничения в виде равенств (2.29), (2.30) накладываются на активные и реактивные мощности в узлах потребления (нагрузки) ![]() и активные мощности в узлах генерации
и активные мощности в узлах генерации ![]() . Простые режимные ограничения (2.31) - (2.33), удерживающие оптимизируемые переменные в допустимых пределах, накладываются на реактивные мощности источников
. Простые режимные ограничения (2.31) - (2.33), удерживающие оптимизируемые переменные в допустимых пределах, накладываются на реактивные мощности источников ![]() , напряжения во всех
, напряжения во всех ![]() пунктах сети и коэффициенты трансформации в
пунктах сети и коэффициенты трансформации в ![]() регулируемых трансформаторах.
регулируемых трансформаторах.
В общем случае балансовые ограничения (2.29), (2.30) контролируются на каждом шаге оптимизации с помощью уравнений установившихся режимов, нарушение простых ограничений (2.31) - (2.33) – добавкой к целевой функции (2.28) штрафной составляющей или (и) фиксацией переменных на нарушенных граничных значениях, сопровождаемых сменой состава зависимых и независимых переменных (смена базиса). Так при нарушении ограничений (2.31), реактивная мощность источников закрепляется на нарушенных пределах с увеличением на величину ![]() количества ограничений (2.30). Выход за пределы напряжения в
количества ограничений (2.30). Выход за пределы напряжения в ![]() м генераторном узле учитывается заменой (добавкой) соответствующего уравнения в системе (2.30) уравнением вида
м генераторном узле учитывается заменой (добавкой) соответствующего уравнения в системе (2.30) уравнением вида
![]() ,
, ![]() .
.
При этом на каждом шаге оптимизации производится анализ возможности снятия переменных с предела, соответственно корректируя количество ![]() балансовых уравнений (2.29).
балансовых уравнений (2.29).
Постановка и решение оптимизационной задачи возможны только при ненулевой степени ее свободы
![]() ,
,
наибольшая величина которой проявляется при отсутствии закрепленных на предельных значениях реактивной мощности или напряжений источников (![]() ) и коэффициентов трансформации регулируемых трансформаторов (
) и коэффициентов трансформации регулируемых трансформаторов (![]() ) и равна количеству независимых переменных (
) и равна количеству независимых переменных (![]() +
+![]() ).
).
Фиксация независимых оптимизируемых переменных во всех узлах генерации (![]() или
или ![]() ,
, ![]() ) на соответствующих пределах сводит задачу оптимизации (2.28) - (2.33) к решению 2
) на соответствующих пределах сводит задачу оптимизации (2.28) - (2.33) к решению 2![]() -мерной системы нелинейных УУР (2.29), (2.30).
-мерной системы нелинейных УУР (2.29), (2.30).
Методика решения предусматривает на каждом шаге оптимизации:
а) расчет установившегося режима при заданных значениях регулируемых параметров и определение значения целевой функции;
б) выполнение шага оптимизации, на котором происходит изменение регулируемых (независимых) параметров;
в) сопоставление целевой функции с предыдущим значением.
Решение данной оптимизационной задачи выполняется, как правило, на основе градиентных методов в детерминированной или стохастической постановках /11, 12/.
0 комментариев