Дисперсию входного шума определяют по формуле

2.         Дисперсию входного шума определяют по формуле

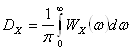, (3.4)

где - энергетический спектр шума.

Интегрировать будем ,по условию задачи, в полосе частот . ,

поскольку спектр шума равномерен, а за пределами этой полосы – равен нулю. Определим дисперсию входного шума по формуле (3.4) с помощью [3]:

D_x=0.125 В².

Вычислим амплитуду несущего колебания  в соответствии с задачей по формуле :

. (3.5)

Подставив исходные значения получим: =3.537 В.

3. Определяем отношение сигнал/помеха на входе (по мощности) детектора :

. (3.6)

Подставив исходные значения получим::  h=50

Определяем отношение сигнал/помеха на выходе детектора по формуле :

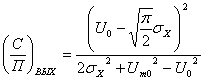, (3.7)

где - среднеквадратическое отклонение входного шума;

 - постоянная составляющая выходного напряжения детектора при одновременном воздействии сигнала (несущей) и шума. Сначала находим СКО=0.354 В. Далее определяем постоянную составляющую  формуле

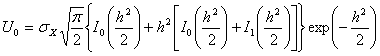, (3.8)

где -функции Бесселя нулевого и первого порядков (модифицированные) соответственно. Производим вычисления с помощью [3] находим =3,555 В. Подставляем полученные значения , СКО находим, что сигнал/помеха на выходе равен:

4. Напряжение на выходе детектора в отсутствии шума прямопропорционально амплитуде  входного сигнала

,  (3.9)

где - коэффициент преобразования детектора, который определяется по формуле:

 .  (3.10)

 где Q-угол отсечки.

Угол отсечки тока определим решением трансцендентного уравнения:

. (3.11)

Решение уравнения (3.11) произведем в [3].Решив (3.11) находим Q=21.83, а К0=0.928.

Раскрыв скобки в выражении (3.9), приведём выражение для выходного сигнала к виду

, (3.12)

где: - постоянная составляющая выходного сигнала;

- амплитуда выходного сигнала.

Подставив значения, получим:

Построим сигнал на выходе детектора:

. (3.13)

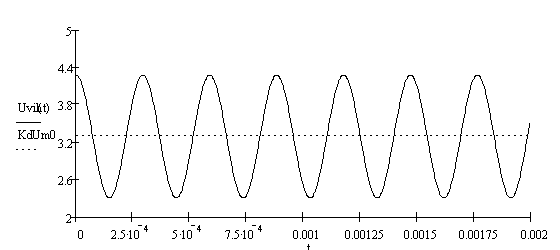
Рисунок 3.2 - График сигнала на выходе детектора.

Изобразим ВАХ диода, а также временные диаграммы тока диода и напряжения на диоде:

Рисунок 3.3 – График ВАХ диода, временные диаграммы тока диода и напряжения на диоде

Задание №4

Генератор на полевом транзисторе с контуром в цепи стока генерирует гармоническое колебание с частотой . Контур состоит из индуктивности L, емкость C и имеет добротность Q. Крутизна сток-затворной характеристики транзистора в рабочей точке S.

Условие:

1.     Изобразить электрическую схему генератора. Записать дифференциальное уравнение и вывести условие самовозбуждения генератора.

2.     Определить критические коэффициенты включения .

3.     Выбрать значение P, обеспечивающее устойчивую генерацию и рассчитать неизвестный элемент контура.

4.     Изобразить качественно процесс установления колебаний в генераторе, указать области нестационарного и стационарного режимов.

Исходные данные:

Индуктивная трехточечная схема;

 

Решение:

1. Представим принципиальную схему индуктивного трехточечного автогенератора [2]:

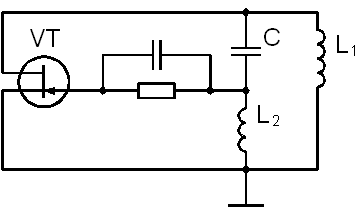
Рисунок 4.1 – Автогенератор, собранный по индуктивной трехточечной схеме.

Для составления дифференциального уравнения генератора рассмотрим колебательный контур подробнее, при этом как бы разорвав обратную связь (рисунок 4.2).

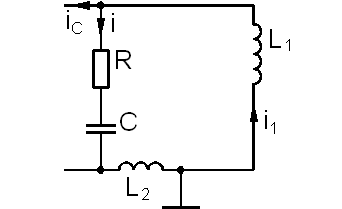
Рисунок 4.2 – Колебательный контур автогенератора.

В схеме на рисунке 4.2 R – сопротивление потерь контура.

По законам Кирхгофа и, используя компонентные уравнения элементов запишем систему характеристических уравнений [6] цепи представленной на рисунке 4.2.

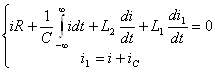. (4.1)

Для решения системы (4.1) не хватает еще одного уравнения. Его мы возьмем воспользовавшись характеристиками транзистора:

. (4.2)

Теперь проведя необходимые подстановки запишем уравнение с одним неизвестным током i.

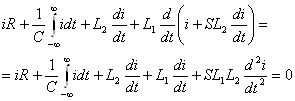. (4.3)

Чтобы избавиться от интеграла продифференцируем уравнение (4.3) по времени.

.  (4.4)

Обозначим коэффициенты при неизвестном и его производных, как  и  соответственно при дифференциалах 0-ого, 1-ого, 2-ого и 3-его порядков. Тогда (4.4) примет вид:

. (4.5)

Для определения условия самовозбуждения воспользуемся критерием устойчивости Рауса-Гурвица [2]. В соответствии с этим критерием, для самовозбуждения необходимо и достаточно чтобы выполнялось:

1) 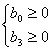;  (4.6)

2) .  (4.7)

Подставляя значения коэффициентов , получим условие самовозбуждения автогенератора.

. (4.8)