Рассчитать и построить импульсную характеристику фильтра

5. Рассчитать и построить импульсную характеристику фильтра.

6. Рассчитать и построить выходной сигнал цифрового фильтра, если на вход подаётся дискретный сигнал из задания 5.

Исходные данные:

Решение:

1. Данный фильтр реализовывается с помощью рекурсивного фильтра 1-го порядка. Схема данного фильтра представлена на рисунке 6.1:

Рисунок 6.1 - Рекурсивный фильтр

2. Передаточная функция цифрового фильтра имеет вид:

 , (6.2)

где а_к, b_k коэффициенты уравнения; - интервал дискретизации; - количество элементов задержки в трансверсальной части; - количество элементов задержки в рекурсивной части.

Найдём полюса передаточной функции с помощью формулы:

(6.3)

Для нахождения полюсов воспользуемся [3]:

Для обеспечения устойчивости необходимо и достаточно, чтобы полюса передаточной функции находились в левой полуплоскости комплексного переменного p. Поскольку

 - система устойчива.

3. С помощью [3] рассчитаем и построим АЧХ и ФЧХ фильтра:

(6.4)

Для данной передаточной функции с помощью [3] построим АЧХ и ФЧХ фильтра (рисунок 6.2):

 

Рисунок 6.2 - а) АЧХ фильтра; б) ФЧХ фильтра.

4. Найдем системную функцию фильтра путем замены e^PT на Z. Системная функция будет иметь вид:

(6.5)

Устойчивость фильтра оценивается расположением полюсов системной функции на z плоскости. Фильтр устойчив, если полюса системной функции расположены внутри круга единичного радиуса с центром в точке .

 Определим полюса системной функции в плоскости Z с помощью [3]:

 - т.е. система устойчива.

5. Импульсная характеристика - это реакция цифрового фильтра на воздействие в виде единичного импульса  (функция Кронекера). Используя уравнение цифровой фильтрации, получаем:

(6.6)

где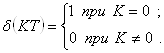

 

Для данного фильтра импульсная характеристика будет определятся формулой:

(6.7)

График импульсной характеристики представлен на рисунке 6.4:

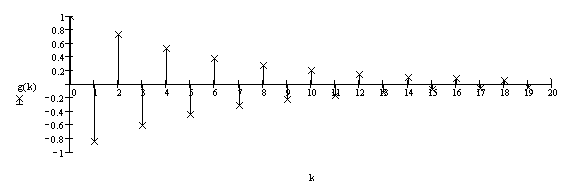
Рисунок 6.4.-Импульсная характеристика.

6. Графики входного дискретного сигнала и выходного цифрового сигнала (рисунок6.3):

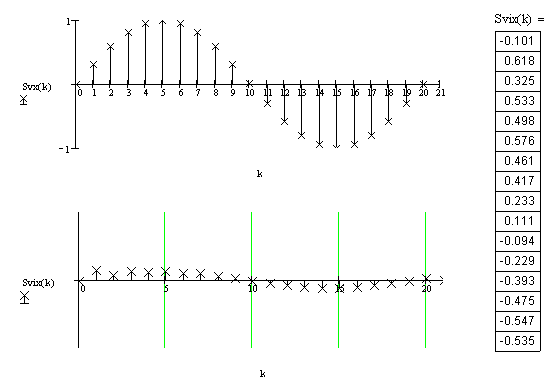
Рисунок 6.3 - а) входной дискретный сигнал; б) выходной цифровой сигнал.

Задание №7

Условие:

Синтезировать согласованный фильтр для данного сигнала.

Требуется:

1.     Определить комплексный коэффициент передачи фильтра.

2.     Синтезировать структурную схему фильтра.

3.     Определить и построить выходной сигнал (под входным).

4.     Оценить отношение сигнал/помеха на выходе в зависимости от .

Исходные данные:

Когерентная пачка из  радиоимпульсов с прямоугольной огибающей и скважностью равной ,

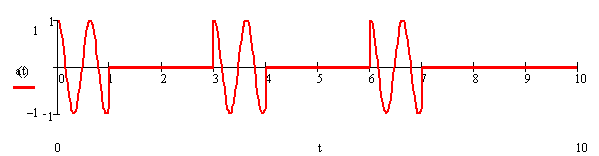
Рисунок 7.1 – Входной сигнал

 

Решение:

1. Синтезировать согласованный фильтр удобно при помощи его комплексного коэффициента передачи. Запишем общую формулу для его определения [2]:

. (7.1)

Где  - постоянный коэффициент;

 - функция, комплексно сопряженная со спектральной плотностью входного сигнала;

 - время задержки пика выходного сигнала.

Для  существует ограничение - , это связано с физическими принципами работы согласованного фильтра [2]. Однако обычно полагают:

. (7.2)

Из формулы (7.1) видно, что задача сводится к определению спектральной плотности входного сигнала. Для ее определения разобьем входной сигнал на отдельные импульсы, затем определим спектр одного из них, а результат запишем в виде суммы вышеопределенных спектральных плотностей всех составляющих пачки, но сдвинутых по времени на расстояния кратные периоду их следования.

Итак, определим  - спектр одиночного радиоимпульса, путем применения свойства [2], в котором говорится, что спектр радиосигнала это есть спектр его огибающей только сдвинутый в область высоких частот (окрестность ).

. (7.3)

Где  - спектральная плотность для огибающей одиночного радиоимпульса, смещенная в область ВЧ на .

Запишем аналитическое выражение для огибающей радиоимпульса:

. (7.4)

Определим , для этого применим прямое преобразование Фурье [7].

;

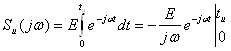. (7.5)

Представим формулу для , заменив в (7.5)  на :

. (7.6)

Т. о. спектральная плотность всей пачки импульсов будет определяться как сумма спектральных плотностей определяемых формулой (7.6), но сдвинутых друг относительно друга на:

.  (7.7)

Представим это соотношение, применив теорему сдвига [2]:

. (7.8)

Запишем формулу комплексно сопряженной спектральной плотности входного сигнала, преобразовав (7.8), путем перемены знака мнимой части.

. (7.9)

Подставим (7.6) в (7.9), а полученный результат в (7.1) и проведем некоторые преобразования для удобства ее дальнейшего использования:

(7.10)

2. Т. о. согласованный фильтр можно представить как каскадное соединение двух блоков:

1. согласованный фильтр одиночного радиоимпульса;

2. т. н. синхронный накопитель (многоотводная линия задержки).

Схема такого фильтра представлена на рисунке 7.2.

2Т

Т

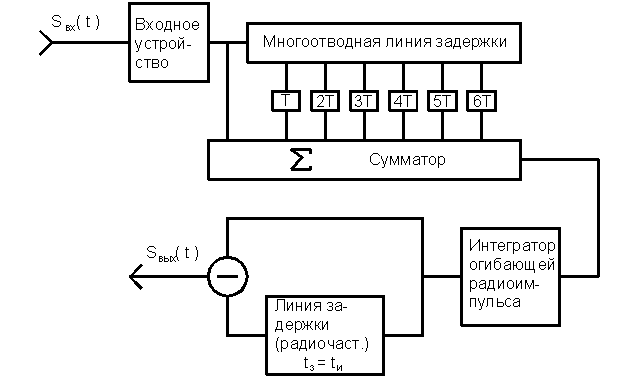
Рисунок 7.2 – Структурная схема согласованного фильтра для сигнала представленного на рис. 7.1.

График когерентной пачки радиоимпульсов проходящей через линию задержки представлен на рисунке (7.3).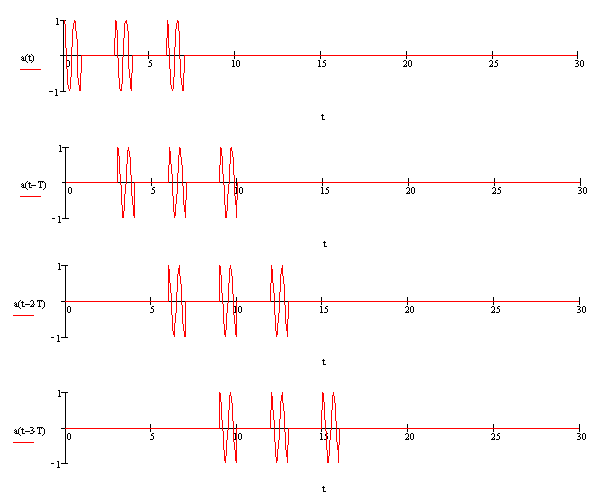

Рисунок 7.3 - График пачки радиоимпульсов, проходящих через линию задержки

Сигнал на выходе согласованного фильтра с точностью до константы совпадает с автокорреляционной функцией входного сигнала, сдвинутой на  в сторону запаздывания [2].

АКФ пачки радиоимпульсов с прямоугольной огибающей представляет собой последовательность треугольных импульсов длительностью  и максимумом равным , где n –количество импульсов пачки, Э₁ – полная энергия одного импульса (максимум АКФ одиночного импульса).

Для начала рассчитаем АКФ одиночного радиоимпульса.

Как известно АКФ радиосигнала равна произведению АКФ огибающей на АКФ несущей [1]:

. (7.11)

Поскольку АКФ несущего колебания есть само это колебание нулевой начальной фазой и амплитудой равной 1, то можно записать:

. (7.12)

Рассчитаем АКФ огибающей :

. (7.13)

Подставим (7.13) в (7.12):

. (7.14)

3. При помощи (7.14) и приведенных выше условий с помощью [3] построим график выходного сигнала и АКФ (рисунок 7.4):

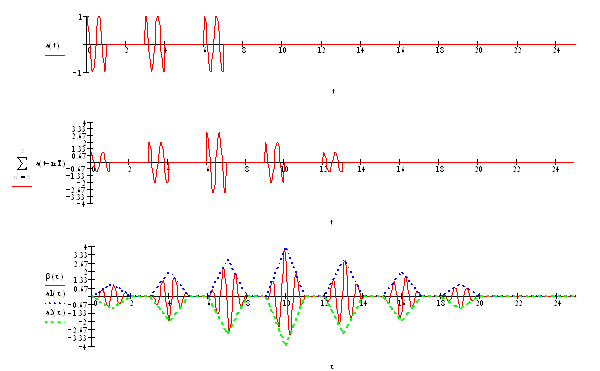Рисунок 7.4 –а) входной сигнал, б) сигнал на выходе согласованного фильтра; в)АКФ сигнала

4. Отношение сигнал/помеха на выходе согласованного фильтра равно:

. (7.15)

Где Э – полная энергия входного сигнала;

W₀ – спектральная плотность мощности белого шума на входе фильтра.

Величина полной энергии входного сигнала с точностью до константы совпадает со значением выходного сигнала при  (по свойствам АКФ).

. (7.16)

Из формул (7.15) и (7.16) видно, что при увеличении n – количества и скважности импульсов пачки входного сигнала соотношение сигнал/помеха на выходе фильтра увеличивается, что соответствует теории поскольку при этом растет база сигнала. Однако данный способ повышения выигрыша по величине отношения  не улучшает корреляционных свойств сигнала, из-за чего через пороговое устройство может проходить не один, а несколько импульсов и отметок на экране индикаторного устройства так же будет несколько. Т. о. кроме увеличения базы сигнала необходимо еще и улучшать его корреляционные свойства.

ПЕРЕЧЕНЬ ССЫЛОК

1.     Гармаш М. А. Конспект лекций по дисциплине СиПРТ (1,2 часть).

2.     Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов.4-е издание, перераб. и доп.-М.:Радио и связь,1986.- 512с.

3.     Математический пакет MathCAD 2000.

4.     Гимпилевич Ю.Б., Афонин И.Л. методические указания к выполнению курсовой работы по дисциплине СиПРТ для студентов специальности 7.090701-“Радиотехника” (дневная форма обучения).