Навигация
Определим максимальную частоту в спектре аналогового сигнала по уровню 0,1
2. Определим максимальную частоту в спектре аналогового сигнала по уровню 0,1.
![]() (5.4)
(5.4) 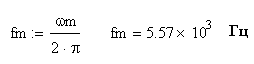 . (5.5)
. (5.5)
3. Условие выбора интервала дискретизации возьмем из теоремы Котельникова :
![]() . (5.6)
. (5.6)
Подставив значения, получим:
![]()
![]()
Воспользовавшись (5.6) выберем интервал дискретизации:
![]()
В этом случае количество выборок определяется следующим образом:
![]() .
(5.7)
.
(5.7)
N = 21;
Теперь, когда мы нашли интервал дискретизации и количество выборок построим график дискретного сигнала, а так же для сравнения в одном масштабе с ним график аналогового (рисунок 5.3):

Рисунок 5.3 – Графики: а) аналогового сигнала;
б) дискретного сигнала.
На рисунке 5.3 в величине выборок отражен весовой коэффициент δ - импульсов дискретизации.
4. Спектр дискретного сигнала, как известно, представляет собой сумму копий спектральных плоскостей исходного аналогового сигнала, подвергнутого дискретизации, сдвинутых на величину частоты следования выборок друг относительно друга [7].
Т. о. Формула спектральной плотности дискретного сигнала примет вид:
![]() . (5.8)
. (5.8)
Пользуясь (5.8) построим график при помощи [3]:
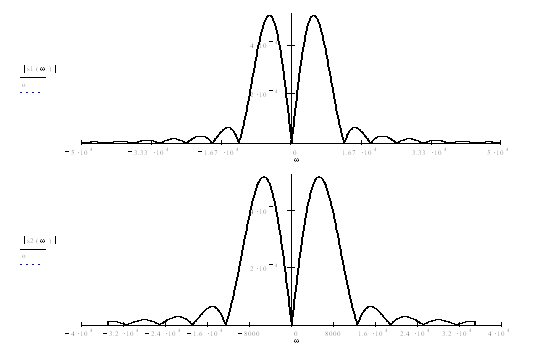

Рисунок 5.4 – а) модуль спектральной плотности аналогового сигнала; б) ограниченный спектр аналогового сигнала;
в) спектральная плотность дискретного сигнала;
5. Дискретное преобразование Фурье определяется формулой (5.9) [2]:
![]() . (5.9)
. (5.9)
Где: ![]() - номер отсчета спектральной плотности;
- номер отсчета спектральной плотности; ![]() ;
;
![]() - номер отсчета дискретного сигнала;
- номер отсчета дискретного сигнала; ![]() .
.
Т. о. по формуле (5.9) и при помощи [3] можно подсчитать значения дискретных отсчетов:

Зная, что выше вычисленные отсчеты следуют через интервалы ![]() , величина которых определяется следующим соотношением [2]:
, величина которых определяется следующим соотношением [2]:
![]() , (5.10)
, (5.10)
где: N – количество выборок дискретного сигнала;
Т – период дискретизации;
можно построить спектрограмму модулей этих коэффициентов.
Данную спектрограмму будем строить в одном частотном масштабе с графиками спектров аналогового и дискретного сигналов и расположив ее под ними.

Рисунок 5.5 – а) Спектр аналогового сигнала;
б) Спектральная плотность дискретного сигнала;
в) Спектрограмма модулей коэффициентов ДПФ.
6. Заменив в формуле (5.9) ![]() на Z (в данном случае
на Z (в данном случае ![]() играет роль частоты) прейдем к выражению для Z-преобразования.
играет роль частоты) прейдем к выражению для Z-преобразования.
![]() . (5.11)
. (5.11)
Распишем (5.11) подробнее, при этом заметим, что как видно из рисунка 5.3 отсчеты с номерами от 0 до 8 равны 1, а 9 равен 0. С учетом всего сказанного получим:
![]() . (5.12)
. (5.12)
При помощи простых математических преобразований представим (5.12) в виде дробно-рационального выражения:
![]() . (5.13)
. (5.13)
Задание №6.
Условие:
Уравнения цифровой фильтрации имеют вид:
![]() (6.1)
(6.1)
Требуется:
1. Составить структурную схему фильтра.
2. Найти передаточную функцию фильтра. Определить полюса передаточной функции и нанести их на ![]() - плоскости. Сделать вывод об устойчивости.
- плоскости. Сделать вывод об устойчивости.
3. Рассчитать и построить АЧХ и ФЧХ фильтра.
4. Найти системную функцию фильтра. Определить полюса системной функции и нанести их на ![]() - плоскости. Сделать вывод об устойчивости.
- плоскости. Сделать вывод об устойчивости.
0 комментариев