Навигация
2 Выбор схемы фильтра
Расчёт порядка фильтра
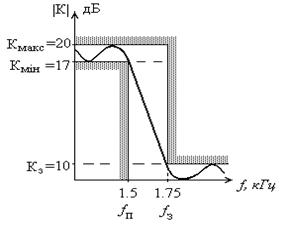
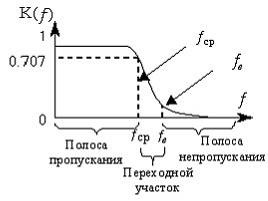
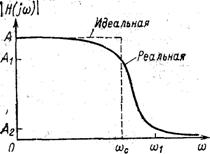
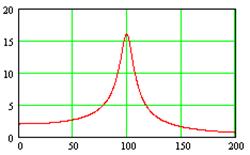
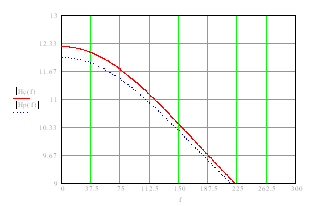
Рисунок 2.1 – Шаблон коэффициента передачи фильтра
Шаблон передаточной функции ФНЧ для заданных значений K и f показан на рис.2.1.
Рассчитаем нормированные коэффициенты передачи и граничные частоты схемы:
Кнmax = Кmax – Кmin=20-17=3 (Дб); Кнmin = Кmax - Kз=20-10=10 (Дб);
¦пн =¦п /¦п =1;¦зн =¦з/fп=1,75/1,5=1,167.
Определим порядок проектируемого фильтра из следующей формулы:
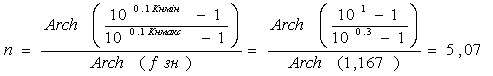 (2.1)
(2.1)
Округлив до большего целого значения, окончательно получим порядок фильтра n=6.
Передаточная функция устройства
Передаточная функция нормированного фильтра выглядит так:
![]() (2.2)
(2.2)
Из таблиц полиномов фильтра Чебышева находим значения числителя и знаменателя передаточной функции для фильтра 6 порядка. Подставим их в выражение 2.2:
![]() (2.3)
(2.3)
Перейдём обратно от нормированного ФНЧ к проектируемому, для чего рассчитаем передаточную функцию проектируемого фильтра:
![]() (2.4)
(2.4)
Найдём числитель функции по формуле:
![]() (2.5)
(2.5)
Чтобы определить знаменатель функции, рассчитаем значение частоты wп=2p¦п=9420 [рад/с]. Сделаем замену в полиноме D1(p): р®р/wп. Окончательно передаточная характеристика будет выглядеть так:
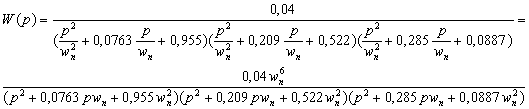 (2.6)
(2.6)
Переход от передаточной функции к схеме
Так как порядок всего фильтра равен 6, для его создания будем использовать три звена второго порядка.
Представим передаточную функцию ФНЧ-6 в виде сомножителей второго порядка:
![]() (2.7)
(2.7)
Определим W(p) для каждого звена:
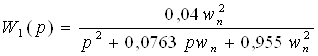 (2.8)
(2.8)
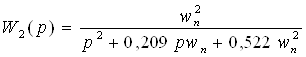 (2.9)
(2.9)
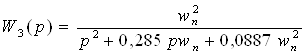 (2.10)
(2.10)
Таким образом, граф Мезона для всей схемы будет представлен в виде последовательного соединения ФНЧ- ІІ, как на рис. 2.2:

Рисунок 2.2 – Структурная схема графа Мезона
Выбор схемного решения
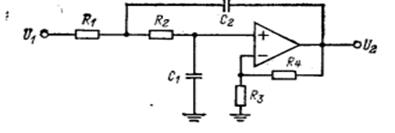
Схемным решением для данного устройства будет фильтр низкой частоты второго порядка с многопетлевой обратной связью, т.к. он обеспечивает небольшую чувствительность к отклонению номиналов элементов. Используем 3 таких звена, соединённых последовательно.
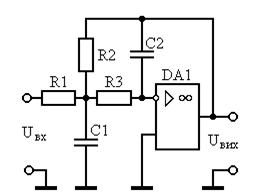
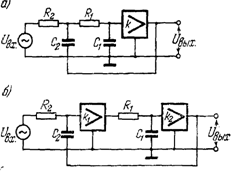
Рисунок 2.3 – ФНЧ-ІІ с многопетлевой обратной связью
3 Топологическая модель фильтра
Граф Мезона ФНЧ- ІІ.
Изобразим граф Мезона для одного звена схемы.
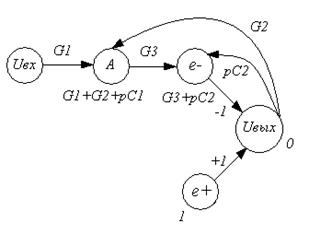
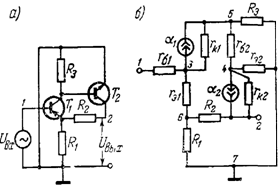
Рисунок 3.1 – Граф Мезона ФНЧ-ІІ
По формуле Мезона рассчитаем передаточную функцию:
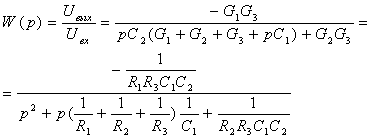 (3.1)
(3.1)
Сопоставим с её канонической формулой для ФНЧ-ІІ:
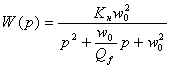 (3.2)
(3.2)
Откуда получим:
K=R2/R1; (3.3)
 (3.4)
(3.4)
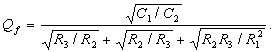 (3.5)
(3.5)
4 Расчет элементов схемы
В соответствии с полученными передаточными функциями, рассчитываем значения элементов для каждого звена по следующему алгоритму.
Выбираем значение ёмкости C2 равную 10 нФ. Определяем добротность фильтра по формуле
![]() ,
,
где A и B – числовые значения перед wп2 и рwп в знаменателе W1(р). Находим ёмкость C2 из соотношения С1>[4(çКç+1)QF2]C2. Определяем два значения R2 (для разных знаков перед корнем):
![]() (4.1)
(4.1)
Рассчитываем по два значения для R1 и R3:
R1 = R2/К ,R3 = 1/w02 С1С2R2.
Выбираем из двух полученных наиболее подходящий ряд сопротивлений R1, R2, R3.
1-е звено
Qf=12.8; w0=9205 рад/с;
С1>6,8 мкФ; C1=10 мкФ;
R21=663,06 Ом; R11=16580 Ом;R31=177,97 Ом;
R22=185,09 Ом; R12=4627,18 Ом;R32=637,56 Ом;
Выбираем первый ряд сопротивлений.
2-е звено
Qf=3,46; w0=6806 рад/с;
С1>0,956 мкФ; C1=1 мкФ;
R21=2570,8 Ом; R11=2570,8 Ом;R31=839,76 Ом;
R22=1679,5 Ом; R12=1679,5 Ом;R32=1285 Ом;
Выбираем первый ряд сопротивлений.
3-е звено
Qf=1,05; w0=2805,5 рад/с;
С1>87,4 нФ; C1=100 нФ;
R21=23117 Ом; R11=23117 Ом;R31=5495,9 Ом;
R22=10991,7 Ом; R12=10991,7 Ом;R32=11558,7 Ом;
Выбираем первый ряд сопротивлений.
Согласуем номера элементов в звене с нумерацией в схеме фильтра, а номиналы сопротивлений – с рядом Е12:
С2=С4=С6=10 нФ;
С1=10 мкФ;C3=1 мкФ;C5=100 нФ;
R1=15 кОм;R2=680 Ом;R3=180 Ом;
R4=2,7 кОм;R5=2,7 кОм;R6=820 Ом;
R7=22 кОм;R8=22 кОм;R9=5,6 кОм;
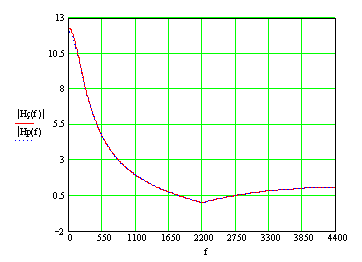
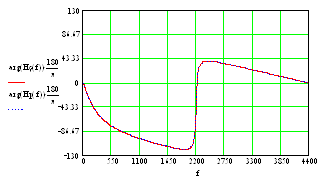
Снимаем АЧХ фильтра для полученных значений элементов.
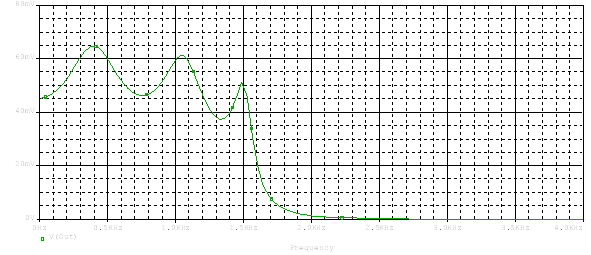 |
Рисунок 4.1 – АЧХ проектируемого фильтра
Похожие работы
... и фильтра верхних частот. Полоса пропускания широкополосный фильтра - образуется благодаря перекрытию полос пропускания ФНЧ (0 -) и ФИЧ (- ) - (рис.7) Рисунок – 7 Образование полосы пропускания широкополосного фильтра 2 Пример расчета фильтра нижних частот на заданные параметры Аналитический метод расчета цепочных фильтров основан на нахождении оптимальных параметров фильтра по ...
... является эллиптический фильтр, характеристики которого значительно лучше характеристик фильтра Чебышева. Рис. 1.5.3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка Рис. 1.5.4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка 1.6 Фильтры нижних частот на ИНУН Схема на ИНУН, реализующая функцию фильтра нижних частот Баттерворта ...
... ; MOV X1, X ; MOV Y1, Y ; RETI ;возврат из подпрограммы обслуживания прерывания по входу END Исходные определения и ручной расчёт результатов работы программы: "Цифровой фильтр (нижних частот)". Разностное уравнение имеет вид: Представим уравнение в виде: , где , 1)Реализуемый коэффициент масштабирования (число без знака) при 8-разрядном формате беззнаковых коэффициентов: ;, ...
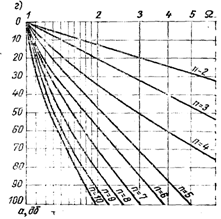
... целесообразно решать аппроксимационную задачу. Определим нормированную частоту ограничения фильтра, как отношение = = 0,6666. Нормированная частота в полосе задерживания обычного фильтра НЧ равна . Эта же частота в случае фильтра НЧ с ограниченной полосой пропускания рассчитывается по формуле Из кривых (рис. 1.) по вычисленной и заданным и а определим ...

0 комментариев