Траектория, линия тока, трубка тока, струя
Основная теорема кинематики (первая теорема Гельмгольца)
Уравнение сплошности
Уравнение движения сплошной среды в напряжениях
Уравнение движения идеальной жидкости (Эйлера) в форме Громека
Основные понятия и определения потенциальных течений
Частные случаи плоских потенциальных течений
Обобщенный закон Ньютона
Подобие гидродинамических явлений
Моделирование ГГД явлений
Переход ламинарного ПС в турбулентный
Навигация
Уравнение движения идеальной жидкости (Эйлера) в форме Громека
Основы гидрогазодинамики
42494
знака
0
таблиц
14
изображений
12. Уравнение движения идеальной жидкости (Эйлера) в форме Громека
Все преобразования выполним на первом уравнении:
Отсюда:
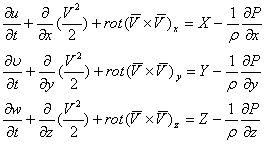
- система уравнений движения для и.ж. в форме Громека
Рассмотрим далее движение, предполагая, что массовая сила имеет потенциал и течение баротропное.
Первое предположение утверждает, что у массовых сил имеется потенциал, связанный соотношениями с массовыми силами:
; 
; 
,
U - потенциал массовых сил.
Второе: баротропным считается течение, у которого ρ считается только функцией давления.
Например, баротропными течением является:
1) ρ=const – газ или жидкость несжимаемы
2) движение среды изотермическое - 
3) движение среды адиабатное - 
Условие баротропности предполагает, что существует некоторая функция Р, зависящая от давления, которая определяется выражением:
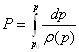
Функция Р связана с р и ρ соотношениями:
; 
; 
.
Подставим в систему уравнений Громека потенциал массовых сил и функцию Р:
- система уравнений Эйлера в форме Громека
Достоинство системы заключается в том, что отдельно выделен ротор, который при определенных условиях может быть равен нулю и система значительно упрощается. Последний член равен нулю, если: 1) 
- статическая задача; 2) 
- течение безвихревое или потенциальное.
Сумма, стоящая во второй компоненте, имеет определенный физический смысл. В векторной форме система может быть записана в виде одного уравнения:
13. Теорема Бернулли
Рассмотрим стационарное баротропное течение под действием массовых сил, т.е. можно записать:
умножим уравнение скалярно на вектор скорости, тогда последний член равен нулю, т.к. идет скалярное перемножение перпендикулярных векторов.
- единичный вектор в направлении вектора скорости. Вектор скорости направлен по касательной к линии тока или к траектории, т.к. течение стационарное, следовательно:
- производная по направлению.
выражение отражает теорему Бернулли: при стационарном баротропном течении идеальной жидкости под действием потенциальных массовых сил сумма кинетической энергии единицы объема, функции давления приведенного к единице массы потенциала массовых сил сохраняет постоянное значение вдоль любой линии тока.
Если бы скалярно умножили исходное уравнение на вектор угловой скорости, то получили бы аналогичный результат вдоль вихревой линии.
Если течение потенциальное, то и сразу же получается:
и 
во всем потоке, т.е. трехчлен Бернулли сохраняет постоянное значение во всей области потенциального потока.
Рассмотрим потенциальное течение несжимаемой жидкости под действием сил тяжести. Т.к. жидкость несжимаема то 
:
У сил тяжести потенциал равен: 
, z – координата.
(1), 
- удельный вес
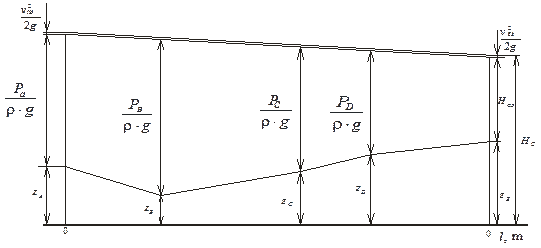
Все эти составляющие имеют размерность давления и называются напорами:
- скоростной или динамический напор; р – пьезометрический напор; 
- геометрический напор; ро – полный напор
При стационарном течении идеальной несжимаемой жидкости полный напор, равный сумме 
, сохраняет постоянное значение вдоль любой линии тока, а при потенциальном течении во всей области потока.
В задачах, в которых можно пренебречь влиянием геометрического напора, уравнение Бернулли упрощается и приобретает вид: 
Уравнение (1) разделим на 
, тогда:
все компоненты измеряются в метрах и называются высотами: 
- скоростная высота, 
- пьезометрическая высота, z – нивелирная высота, Н – гидравлическая высота. При стационарном движении идеальной несжимаемой жидкости высота
сохраняет постоянное значение вдоль любой линии тока (или вихревой линии), а при потенциальном течении во всем токе.
Похожие работы
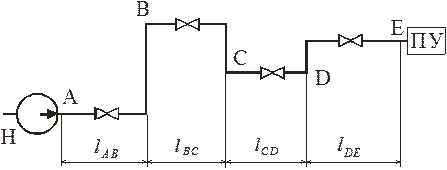
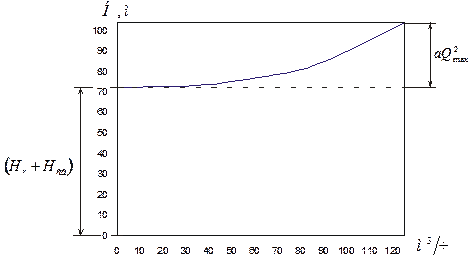
астке СD – 1 шт., на участке DE – 1 шт.; Рис. 1.1. Схема водоснабжения ПУ: Н – насос, ПУ – промышленные установки 3) Напор у потребителя, независимый от потерь напора в трубопроводе ( свободный напор) - ; 4) число часов работы установки в сутки - ; 5) число дней работы установки в году - дней.2. Теоретическая часть По способам ...
... переключения с акустического анализа на прочностной. ProCAST(UES, CALCOM) Согласно исследованиям , проведенными экспертами NASA, ProCAST признана наиболее мощной и корректной программой для расчета литейных процессов. ProCAST позволяет инженеру-проектировщику рассчитывать и визуализировать в трехмерной постановке процесс течения и отверждения металла в форме, предсказывать микроструктуру, ...
... времени на коммуникации) Заметим, что алгоритм EVAH имеет большое преимущество перед традиционными алгоритмами на неориентированных графах именно в силу возможной обработки ориентированного графа. Для многоблочных задач объем коммуникации между соседними блоками не всегда симметричный. Алгоритм EVAH учитывает время на коммуникации, но не пытается распределить блоки на несколько процессоров, ...
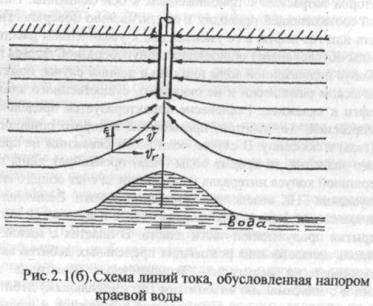
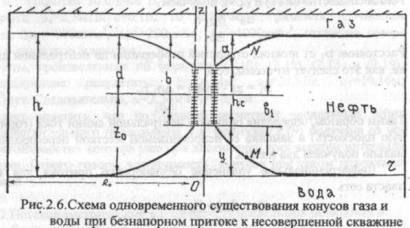
... результаты разработки нефтегазовых и газоконденсатнонефтяных залежей приведены в [47-53]. 2. Моделирование процессов статического конусообразования при разработке нефтегазовых и газоконденсатнонефтяных залежей 2.1 Сущность проблемы конусообразования Большинство нефтяных, газоконденсатнонефтяных, нефтегазовых и газовых залежей, разрабатываемых в настоящее время, подстилаются частично или ...
0 комментариев