Навигация
º
(2.11)
![]()
По концентрации теплового потока в пятне нагрева импульсные плазменные струи приближаются к электронному лучу и намного превосходят стационарные плазменные струи. Тепловые процессы при плазменном поверхностном упрочнении наиболее просто можно вычислить по известным аналитическим выражениям [7], которые представляют собой решение дифференциальных уравнений теплопроводности в линейной постановке при линейных граничных условиях.
Уравнение процесса распространения тепла в массивном полубесконечном теле от мощного быстродвижущегося нормально-распределенного источника нагрева, каким является плазменная струя, имеет вид [7,9]
(2.12)
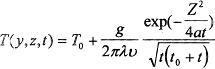
гдеТ - температура нагрева;
у,z - ширина и глубина пятна нагрева;
t - время;
То - температура тела;
g - эффективная мощность плазменной струи;
λ,α - коэффициенты теплопроводности,температуропроводности;
υ - скорость перемещения источников.
Мгновенная скорость охлаждения:
(2.13)
W = dT / dt
Уравнение распространения тепла для случая упрочнения плазменной дугой для точек, расположенных под центром анодного пятна, при скорости перемещения υ<3бм\ч имеет вид [10]
(2.14)
![]()
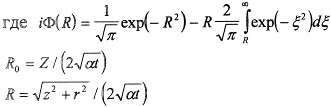
r - радиус анодного пятна;
ξ - координата (глубина).
Расчет по уравнению (2.12 – 2.14) показывает, что температура нагрева материала регулируется в интервале от начальной температуры до температуры плавления, скорость охлаждения от 104 до 106º С\с.
При действии на поверхность полубесконечного тела теплового источника движущегося вдоль оси X, следует различать медленнодвижущийея, быстродвижу-щийся и импульсный источники тепла. Первый случай имеет место тогда, когда теплонасыщение успевает произойти раньше, чем пятно нагрева пройдет расстояние, равное радиусу пятна нагрева. При этом максимальная температура нагрева материала находится в центре пятна нагрева. По мере увеличения скорости перемещения теплового источника максимум температуры сдвигается к краю нагрева, в сторону, противоположную направлению перемещения теплового источника. Если тепловой источник движется с постоянной скоростью, то через определенный промежуток времени температурное поле вокруг движущегося источника стабилизируется. При упрочнении импульсной плазменной струей, время распространения теплового потока соизмеримо со временем воздействия плазменной струи на материал. В реальных условиях после прекращения действия теплового источника происходит выравнивание температуры. При этом в начальный момент времени, после прекращения действия происходит продвижение изотермы с фиксированной температурой в глубь материала и после достижения определенной глубины Zmaxимеет место, обратное перемещению данной изотермы [1,7]. Для одномерного случая температура любой точки материала на оси теплового источника, расположенного ниже плоскости Z= 0, определяется из выражения:
(2.15)
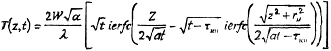
где Z -расстояние по оси;
ierfc - функция интеграла вероятности;
τим - длительность нагрева;
r - радиус пятна нагрева;
а, λ - коэффициенты температуропроводности и теплопроводности. При0 < 1 < τим в уравнении (2.5) приводится к упрощенному виду [1,7]
(2.16)
![]()
Плотность энергии в пятне нагрева W выражается по следующей зависимости:
![]()
гдеgэф - эффективная тепловая мощность плазменной струи(дуги),
τ- длительность нагрева,
d - диаметр пятна нагрева.
С целью последующего вычисления протяженности по глубине зоны нагрева до температуры Т удобно использовать выражение для расчета температур в неявном виде, полученное при допущении τn››√at
(2.17)
![]()
где Z - глубина нагрева до температурыT(z,t);
Из выражения (2.17) можно получить простую формулу определения протяженности по глубине зоны нагрева до заданной температуры за счет плазменного
нагрева.
(2.18)
Z ≈ 2√aτим / π - Тλ /W
Для получения за один проход широкой упрочненной дорожки, при упрочнении применяют сканирование (магнитные или механические системы) плазменной струи (дуги) по поверхности в направление перпендикулярном поступательному перемещению. С целью упрощения модель для приближенной оценки парамет-ров сканирования можно представить в виде плоской задачи.
Известно, что в случае использования модели одновременного нагрева полу» бесконечного тела поверхностным тепловым источником с постоянной во времени интенсивностью, можно получить соотношении плотности мощностиgm, требуемой для достижения на поверхности максимальной температурыТтах
(2.19)
gт=Ттахаср√ π /4 at
где α -температуропроводность;
ср - объемная теплоемкость;
t - времся нагрева.
Для нагрева плазменной струей (дугой)
(2.20)
t = d / υ,g = gn / S
где d - диаметр пятна нагрева в направлении движения;
υ - скорость перемещения пятна, относительно детали;
gn - полная мощность, подводимая к плазмотрону;
S - площадь, обрабатываемая плазменной струей.
В случае упрочнения без оплавления поверхности, необходимо, чтобы Ттах а поверхности! материала не превышала температуру плавления
(2.21)
Ттах≤Тпл
Тогда, согласно (2.19) и (2.21), должно выполняться условие
(2.22)
gт√t ≤ Тпл аср√ π /4 a
где знак равенства соответствует максимальной глубине закалки, без оплавления поверхностности.
Рассмотрим пятно нагрева радиусом r, движущиеся по поверхности металла со скоростью υ и одновременно совершающее пилообразные колебания частотой f и амплитудой 2d перпендикулярно направлению υ, рис. 2.2.
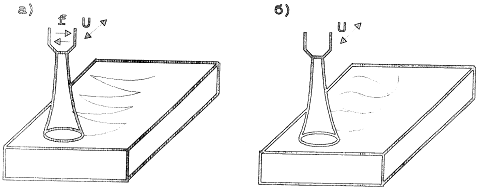
Рис.2.2. Схемы линейного (а) и кругового (б) сканирования.
Сканирующая плазменная струя создает на обрабатываемой поверхности усредненный источник тепла, размерами 2r * 2 d , движущийся со скоростьюυ,
для которого время нагрева определяется соотношением:
t1=2r/υ (2.23)
а плотность мощности: gт = gэф / 4rd
где gэф - эффективная тепловая мощность.
Из (2.22) следует, что для максимальной глубины закалки необходимо, чтобы выполнялось условие:
(2.24)
gт√ t1 = Тпл аср√π / 4а
Кроме того, сканирующая плазменная струя создает концентрированный источник тепла диаметром 2r , скорость которого определяется из амплитуды и частоты колебаний, тогда время нагрева можно записать как:
(2.25)
t2 = 2( 2r / 4df ) = r/df
Множитель 2 означает, что в крайних точках пятно нагрева находится вдвое дольше, чем в промежуточных. Тогда плотность мощности соответственно равна:
( 2.26)
gт2 = gn / πr2
С целью исключения оплавления поверхности в крайних точках необходимо выполнение условия:
(2.27)
g2 √ τ2 ‹ g1 √τ1 ≤ Тпл аср√π / 4а
Амплитуда и частота сканирования должны соответствовать выражениям
(2,28)
√ d /f ‹ πr√8υ
или
![]()
Выражение (2.28) показывает, что частота сканирования должна увеличиваться с уменьшением пятна нагрева, с ростом скорости обработки и амплитуды сканирования. На тепловые процессы и размеры упрочненной зоны, помимо параметров режима работы плазмотрона (сила тока, расход газа и т.) оказывают влияние и параметры ведения технологического упрочнения, такие как скорость обработки, дистанция обработки, угол наклона плазменной струи (дуги) к обрабатываемому изделию и др.
При разработке технологических процессов на практике необходимо иметь простые 9 удобные аналитические выражения для расчета основных параметров упрочнения. В работах по плазменному упрочнению [10, 12 - 14] используются различные аналитические выражения. Так в работе [12] скорость нагрева локальной зоны определяется из выражения:
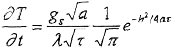
где gs - плотность мощности плазменной дуги;
α, λ- коэффициенты температуропроводности и теплопроводности;
τ - время воздействия;
h- глубина упрочнения.
Значение плотности мощности плазменной дуги достаточнойдля фазовыхпревращений определяют:
![]()
где Тзак - температура закалки;
В - коэффициент аккумуляции теплоты.
Глубина закаленного слоя определяется из выражения:
![]()
где Р - мощность плазменной дуги;
υ - скорость обработки;
d- диаметр пятна нагрева;
ρ - плотность материала;
Ст - удельная теплоемкость;
Q- теплота плавления;
Кв- коэффициент, учитывающий качество обрабатываемой поверхностности.
Скорость обработки определяется как:
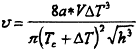
В работе [13] используется зависимость глубины закалки от параметра
h = Р/ (dcυ)0,4
где Р - тепловая мощность источника нагрева;
d - диаметр сопла;
υ - скорость обработки.
В работах Токмакова В.П., Гречневой М.В., Петухова А.В., Скрипкина А.А.,Матханова В.Н. приводятся расчетные данные, позволяющие определить температуру нагрева и скорость охлаждения металла. Построены номограммы для выбора оптимальных режимов плазменного упрочнения. Экспериментальные исследования процесса плазменного упрочнения сталей 9ХФ, 40Х, У8, Х12М,проведенные этими авторами , показали, что максимальная поверхностная твердость после упрочнения пропорциональна величине углеродного эквивалента Сэкв , а глубина упрочнениязависит от коэффициента температуропроводности. Это позволило авторам установить зависимость вида:
HWmax=f (g, υ, Сэкв);h = f2(g, υ, а)
В явном виде уравнения этих зависимостей выглядят следующим образом:
HVmax= 10-3 ﴾-0.308271 υ2+1.23441g2+12.792a2+1.71723 υg- 1.54273 υCэкв – 1.7919 υ+ 0.36981g-18.2439Cэкв+11,223)
h max = 262.506υ2 +50.3667g2 +1466.729а2 +107.754υg + 53.1505υα - 47.1105gа -
- 938.111υ + 199.495g – 5.6734а + 686.691
Полученные результаты, по мнению авторов, свидетельствуют о хорошем совпадении экспериментальных и расчетных данных, что позволяет, не проводя экспериментов, прогнозировать максимальную твердость и глубину упрочненных поверхностей, табл.2.3., 2.4.
Табл.2.3
Экспериментальные и расчетные значения поверхностной твердости HWmax, в зависимости от входных параметров (g, υ , С экв)
| № | V, м/c | g, кВт/м2 | C,% | HVэксп, МПа | HVрас, МПа |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. | 5 5 5 1 1 1 2,5 2,5 2,5 2,5 | 10 15 25 10 15 25 10 15 20 25 | 0,05 1,05 0,9 0,9 0,45 0,6 0,45 0,75 0,6 0,9 | 6000 10500 9000 6700 5900 5300 3100 4200 4900 9800 | 6383 10156 8702 6359 6045 5852 2961 4369 5202 8000 |
Табл.2.4.
Экспериментальные и расчетные значения глубины упрочнения
от hmax входных параметров
| № | υ, м/c | g, кВт/м2 | а, см2/с | hэксп, МПа | hрас, МПа |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. | 0,5 0,5 0,5 0,5 0,5 1,5 1,5 1,5 1,5 2,5 2,5 2,5 2,5 2,5 | 10 15 20 25 30 10 15 20 25 10 15 20 25 30 | 0,1 0,15 0,12 0,06 0,08 0,15 0,08 0,06 0,1 0,06 0,1 0,08 0,12 0,15 | 600 890 920 930 1250 310 250 130 410 45 120 140 330 500 | 623 831 882 945 1167 335 162 173 390 53 196 150 343 529 |
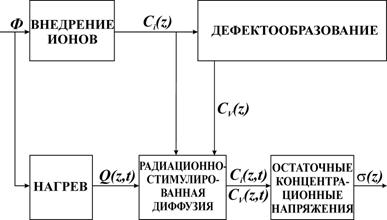
Построение математических моделей плазменного поверхностного упрочнения, отражающих кинетику процесса, основано на решении не линейных краевых задач теории теплопроводности. Корректное описание теплофизических процессов взаимодействия плазменной струи (дуги) с поверхностью обрабатываемого материала, возможно лишь с учетом необратимых процессов, сопровождающих поверхностную закалку детали, полиморфных превращений, окислительных реакций на
поверхности, энергетических потерь на плавление и испарение материала, изменение теплофизических свойств материала при нагреве и охлаждении. В качестве основы такой модели можно использовать «задачу Стефана» со свободной границей σ, являющейся фронтом мартенситного образования. Математическая постановка такой задачи сводится к определению температурных полей в поверхностном слое детали и к расчету границ раздела при полиморфных превращениях. Аналитическое решение возможно только при ряде упрощений. В работе [24] представлена математическая модель плазменного поверхностного упрочнения азотирования из газовой фазы.
Похожие работы
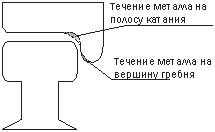
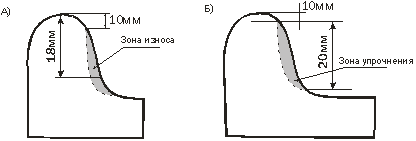
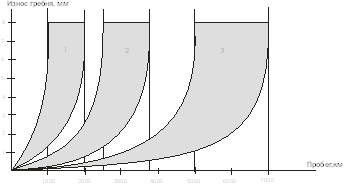
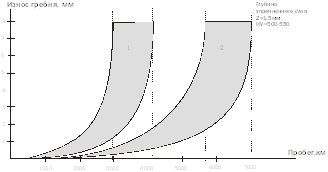
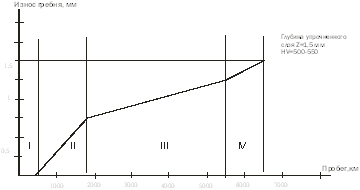
... закалку непосредственно под электровозом или вагоном (без выкатки колесных пар) [1-3]. За восемь лет работы на ВСЖД открыты 12 участков плазменного упрочнения гребней колесных пар и обработано более 35 500 колесных пар. В течение этих лет проводились исследования триботехнических свойств упрочненных колесных пар на фиксированном участке ВСЖД, а именно на горном участке Иркутск-Слюдянка. Выбор ...
... Триботехника,-М.: Машиностроение, 1985. Лахтин Ю.М. и др. Материаловедение: Учебник для ВУЗов, 3е издание. М.: машиностроение 1990. Плазменное поверхностное упрочнение / Лещинский Л.К. и др.- К.: Техника, 1990. Повышение несущей способности деталей машин алмазным выглаживанием / Яценко В.К. и др.- М.: Машиностроение,1985. Упрочнение поверхностей деталей комбинированными способами / А.Г. Бойцов и ...
... перемещения луча приведено на рис. 1.5. Наблюдаемые различия в структуре и твёрдости слоёв зоны в стали 35, обрабатываемой непрерывным излучением лазера на СО2, объясняют различными условиями их нагрева и охлаждения. 1.6. Упрочнение кулачка главного вала В течение последних трёх – пяти лет появились мощные газовые лазеры, обеспечивающие в режиме непрерывной генерации мощность порядка ...
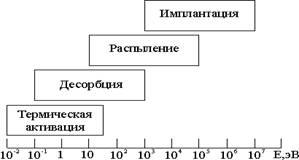
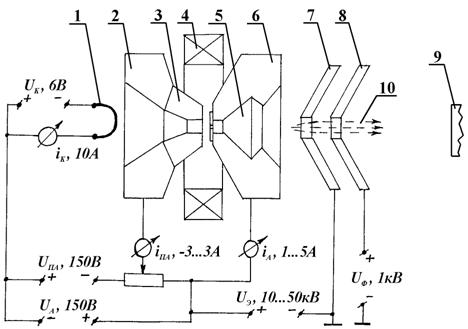
... является то, что рабочий стол 6 с обрабатываемыми образцами 5 размещается внутри данного устройства. Разрабатываемое оборудование позволит осуществлять имплантацию ионов азота с энергией 1 – 10 кэВ ( Дж) в металлы и сплавы, модифицируя их свойства в нужном направлении. Заключение Несмотря на большое количество исследований в области ионной имплантации, остаётся ещё множество вопросов, ...
0 комментариев