У начала пути
Основные понятия
Эффект Мейснера
Сверхпроводники первого рода и второго рода. Абрикосовские вихри
Нулевое сопротивление
Промежуточное состояние при разрушении сверхпроводимости током
Туннельные эффекты
Влияние кристаллической решетки
Энергетическая щель
Теория Гинзбурга – Ландау
Электродинамика сверхпроводников
Глубина проникновения в пипардовских сверхпроводниках
МГД – ЭНЕРГЕТИКА
Навигация
Теория Гинзбурга – Ландау
Сверхпроводники
94355
знаков
0
таблиц
0
изображений
6. Теория Гинзбурга – Ландау.
6.1 Примеры фазовых переходов.
В основе теории Гинзбурга – Ландау лежит теория фазовых переходов Ландау, разработанная им для общей ситуации, когда система претерпевает фазовый переход, при котором состояние системы перехода меняется непрерывно, а симметрия скачком. При этом высокотемпературная, или, как говорят, «парамагнитная» фаза, является более симметричной, а низкотемпературная фаза – менее симметричной, поскольку она проявляет дополнительный порядок, нарушающий симметрию парафазы. При фазовом переходе происходит понижение энергии упорядочной фазы по сравнению с энергией неупорядочной фазы. Примеры фазового перехода весьма разнообразны. К ним относится переход из парамагнитного состояния в ферромагнитное или антиферромагнитное состояние. Для примера на рис. 22 показана конфигурация различных моментов отдельных атомов в упорядочной фазе (рис.22,а) и в разупорядочной (рис.22,б). Если при Т > Тc средний магнитный момент всего кристалла равен нулю, то при Т < Тc возникает предпочтительное направление, выделенное внешним магнитным полем; проекция среднего момента на это направление уже отлична от нуля. Соответственно, если при Т > Тc имелась симметрия по отношению к вращению, то при Т < Тc такая симметрия отсутствует. В общем случае параметром порядка является физическая величина, отличная от нуля в упорядочной фазе и равная нулю в разупорядочной (парамагнитной) фазе. При отходе от точки фазового перехода Тc в глубину упорядочной фазы параметр порядка возрастает. В случае ферромагнетика параметром порядка служит вектор магнитного момента М ¹ 0 при Т < Тc и М = 0 при Т > Тc. Ферромагнетизм широко распространен в природе. Так, примерами металлических высокотемпературных ферромагнетиков (Тc > 300К) являются Fe, Ni, Co. Имеются примеры диэлектрических и полупроводниковых ферромагнетиков. Более сложно организована структура антиферромагнетика. При этом парамагнитная фаза не отличается от паказаной на рис.22,б, а в упорядочной фазе конфигурация магнитных атомов имеет «шахматный» порядок (см.рис.23), когда направление спинов чередуются.
Примерами таких, как говорят, «зеркальных» антиферромагнетиков, являются фториды переходных металлов. Параметром порядка здесь является вектор энтиферромагнетизма L = M1 – M2, то есть разность магнитных моментов двух соединений атомов. В ряде случаев магнитные моменты соседних атомов скошены по направлению друг к другу (см.рис.24), при этом помимо L ¹ 0 возникает и ферромагнитная компонента М = М1 + М2 ¹ 0 (в отличие от зеркальных антиферромагнетиков, где М = 0). Говорят, что в таком случае имеет место слабый ферромагнетизм.
Другим примером фазового перехода второго рода, при котором симметрия меняется скачком, а состояние системы непрерывно, является структурный переход, с которым часто связано возникновение сегнетоэлектрических свойств в кристалле.
6.2 Теория Гинзбурга – Ландау. Свободная энергия сверхпроводника.
Исходным моментом в построении теории среднего поля для сверхпроводников является догадка Гинзбурга и Ландау о том, что явление сверхпроводимости может быть описано в терминах волновой функции сверхпроводящих электронов Ф(r), вступающей в роли параметра порядка. Поскольку в общем случае волновая функция Ф(r) является комплексной, это предположение эквивалентно утверждению о том, что параметр порядка сверхпроводимости является двухкомпонентным.
Так как сверхпроводимость обусловлена образованием конденсата куперовских пар, волновая функция сверхпроводящих электронов может быть выражена через одноэлектронные волновые функции Ф↑ и Ф↓ электронов с противоположно направленными спинами Ф(r) = < Ф↑ Ф↓ >, причем как можно показать модуль этой величины, определяет щель в энергетическом спектре сверхпроводника.
При наличии пространственной неоднородности свободной энергии должно быть добавлено градиентно-слагаемое, пропорциональное êÑФ ê2. Поскольку Ф является волновой функцией электронной пары, выражение êÑФ ê2 ассоциируется с плотностью кинетической энергии сверхпроводящих электронов. По этой причине в плотность свободной энергии сверхпроводящее слагаемое, отвечающее пространственным неоднородностям, войдет в виде
Здесь мы учли, что масса куперовской пары равна 2m, где m – масса электронов. При наличии магнитного поля оператор импульса p = -iħÑ должен быть заменен на оператор обобщенного импульса.
Подчеркнем, что нетривиальным обобщением теории Гинзбурга – Ландау является замена градиентного слагаемого с×(Ñj)2 на слагаемое, содержащее оператор обобщенного импульса куперовской пары. Включение вектор- потенциала электромагнитного поля А в выражение для свободной энергии позволит связать параметр порядка с плотностью сверхпроводящего тока js.
Похожие работы
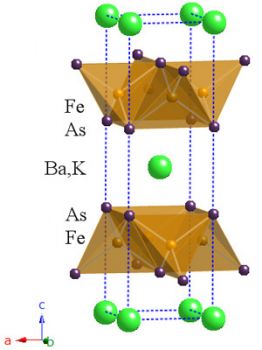
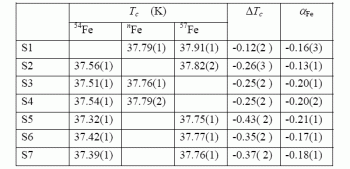
... или он так же пренебрежительно мал, как и в купратных ВТСП? Один из возможных способов решения данной проблемы связан с обнаружением (или необнаружением) изотопического эффекта по железу — веществу, объединяющие «железные» сверхпроводники в один класс. Впервые изотоп-эффект в железосодержащих ВТСП, а точнее, в поликристаллических соединениях SmFeAsO1–xFx (х = 0,15) с Tc = 40 К и Ba1–xKxFe2As2 (х ...
... Исследование процессов на границе сверхпроводника с ферромагнитным металлом привело к необычным результатам: немонотонная зависимость сверхпроводящей критической температуры многослойных структур ферромагнетик (F) - сверхпроводник (S), нетривиальное поведение магнитосопротивления SFS структур и подавление сверхпроводящих свойств в результате спин-поляризованной инжекции. В конце 1998 - начале ...
... ниобия в таблице элементов много проводников, но не сверх. А тепловые колебания их атомов практически такие же. Почему же у других металлов сверхпроводимость не обнаруживается? Тепловые колебания атомов не главный механизм сверхпроводимости! Проводимость конечно зависит от температуры. Но у меди, серебра почему-то при самых низких температурах сверхпроводимость не наблюдается, а у проводника ...
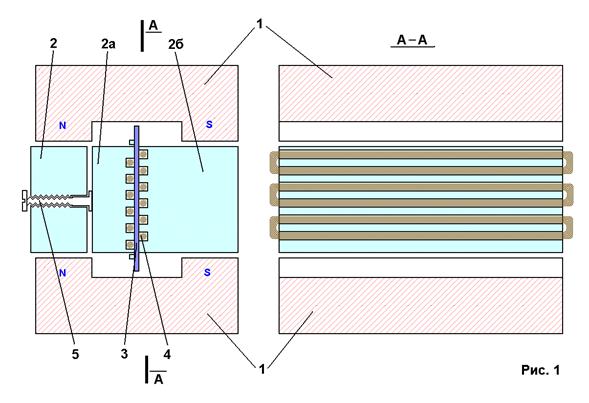
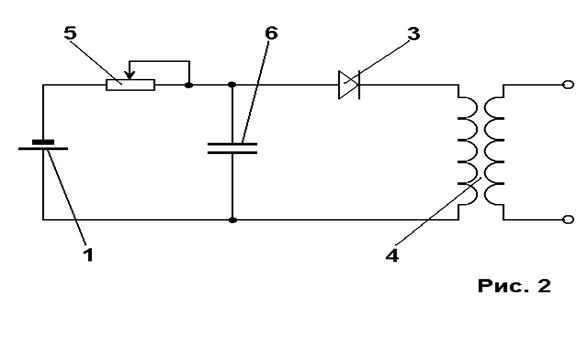
... Полное магнитное сопротивление будет определятся длиной немагнитных зазоров; Rm=L1+L2; Падение напряженности магнитного поля по участкам; Фm=H1/Rm1; H1=ФmxRm 1-первого участка, Фm=H2/Rm2; H2=ФmxRm 2-второго участка, Н1-падение напряженности магнитного поля первого участка, Н2-падение напряженности магнитного поля второго участка. Нс=Н1+Н2. Для работы устройство необходимо три ...
0 комментариев