У начала пути
Основные понятия
Эффект Мейснера
Сверхпроводники первого рода и второго рода. Абрикосовские вихри
Нулевое сопротивление
Промежуточное состояние при разрушении сверхпроводимости током
Туннельные эффекты
Влияние кристаллической решетки
Энергетическая щель
Теория Гинзбурга – Ландау
Электродинамика сверхпроводников
Глубина проникновения в пипардовских сверхпроводниках
МГД – ЭНЕРГЕТИКА
Навигация
Электродинамика сверхпроводников
Сверхпроводники
94355
знаков
0
таблиц
0
изображений
7. Электродинамика сверхпроводников.
Всякая последовательно развивающаяся наука
только потому и растет, что она нужна челове-
ческому обществу.
С.И.Вавилов
7.1 Уравнение Лондонов.
Характерным пространственным масштабом в сверхпроводниках является длина когерентности x- расстояние, на котором движение двух электронов р;
-р¯ носит ещё скоррелированный характер. Здесь мы, предполагая, что все величины медленно меняются на расстоянии x, опираясь на феноменологическую теорию двухжидкостной гидродинамики и используя простые соотношения электродинамики.
Итак, полагая, что все величины плавно меняются в пространстве, плотность свободной энергии в сверхпроводнике при данной температуре запишем в виде
Здесь первое слагаемое представляет собой кинетическую энергию упорядочного движения сверхпроводящих электронов, us - дрейфовую скорость и ns - концентрацию сверхпроводящих электронов, второе слагаемое – плотность энергии магнитного поля, возникающего при наличии сверхпроводящего тока в соответствии с уравнением Максвелла
Плотность сверхпроводящего потока js, в свою очередь, связана с дрейфовой скоростью us простым соотношением
Множитель ns = ns (T) отражает тот факт, что при Т ≠ 0 не все электроны являются сверхпроводящими – в сверхпроводнике имеются квазичастицы, распространение которых связано с диссипацией энергии.
где мы ввели обозначение
Величину lL, обладающую размерностью длины, называют лондоновской глубиной проникновения.
Свободная энергия всего сверхпроводящего образца получается интегрированием e (r) по пространству .
Используем это соотношение для того, чтобы получить уравнение, которому подчиняется распределение магнитного поля Н (r) в сверхпроводнике. Для этого найдем изменение свободной энергии при вариации поля (Н(r) ® Н(r) + s Н(r))
Если рассматриваемый нами сверхпроводник находится в равновесном состоянии, то свободная энергия должна быть минимальна, соответственно вариации свободной энергии вблизи этого состояния должны быть равны нулю
sЕ = 0 заключается в том, чтобы положить равным нулю выражение в круглых скобках в этом уравнении. Тем самым мы получим связь магнитного поля в сверхпроводнике с его пространственными производными – уравнение Лондонов
(7.1)
которое следует дополнить уравнениями Максвелла, в статическом случае имеющими вид
(7.2 а)
(7.2 б)
Выписанная система уравнений позволяет рассчитать распределение магнитного поля Н и сверхпроводящего тока js в равновесном состоянии сверхпроводника.
7.2 Эффект Мейснера.
Применим уравнения (7.1 – 7.2) к задаче о распределении магнитного поля внутри сверхпроводника. Рассмотрим простейший случай, когда сверхпроводник занимает полупространство (z > 0); плоскость х,y является поверхностью сверхпроводника. Рассмотрим вначале случай, когда магнитное поле Н направлено нормально к поверхности Н = (О, О, Н).
Магнитное поле внутри сверхпроводника, если оно достаточно мало, не может обладать отличной от нуля компонентной, перпендикулярной поверхности. Оговорка, касающаяся относительной малости поля, обусловлена тем, что уравнения Лондонов справедливы при плавном изменении Н(r). При достаточно больших значениях поля это условие нарушается (сверхпроводимость разрушается частично или полностью).
Если эффективная масса электронов в сверхпроводнике велика, а электронная плотность, напротив, мала, то соответственно увеличивается глубина проникновения. Отметим также, что поскольку число сверхпроводящих электронов зависит от температуры, обращаясь в нуль при Т= Тc, то сила проникновения увеличивается при увеличении температуры.
Все величины в сверхпроводнике – магнитное поле Н(r), плотность сверхпроводящего тока, скорость направленного движения сверхпроводящих электронов – имеют характерный масштаб изменения порядка lL. Этот вывод справедлив и для сверхпроводников конечного объема.
Тем самым мы уточнили утверждение, которое сделал Мейсснер и Оксенфельд на основе своих экспериментов по поведению сверхпроводника в магнитном поле. В действительности, в поверхностный слой поле проникает, но толщина этого слоя J ~ 10-4см весьма мала, так что магнитным потоком, сосредоточенным в том слое можно пренебречь.
С другой стороны в чистом сверхпроводнике движение двух электронов скоррелировано на расстоянии. В этом случае действительно все макроскопические величины меняются плавно на масштабе скоррелированной электронной пары (куперовские пары). Таким образом уравнения электродинамики в данном случае являются локальными.
Сверхпроводники в которых выполнено неравенство lL >> x, называют лондоновскими сверхпроводниками или сверхпроводниками второго рода. В высокотемпературных оксидных сверхпроводниках YВaCuO величина x состовляет 4 – 20А0 в зависимости от кристаллографического направления, а магнитная глубина проникновения, как показывают эксперименты по деполяризации m - мюонов, порядка 1500А0. Следовательно, такие сверхпроводники являются сверхпроводниками лондоновского типа (рис.25,а). Аналогичным образом обстоит дело с висмутовым и таллиевыми семействами. Отметим , что в сверхпроводниках второго рода во всем диапазоне изменения температуры 0 < Т < Тc температурная зависимость лондоновской глубины проникновения lL хорошо описывается формулой вида
Наличие высокой степени температурной зависимости lL (Т) приводит к тому, что если при подходе к Тc величина lL (Т) обращается в бесконечность. В чистых же низкотемпературных сверхпроводников, напротив, характерным является выполнение противоположного равенства lL << x0. Такие сверхпроводники называются сверхпроводниками первого рода (пипардовскими сверхпроводниками).
Похожие работы
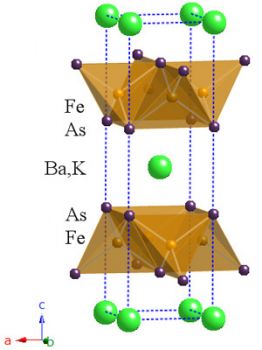
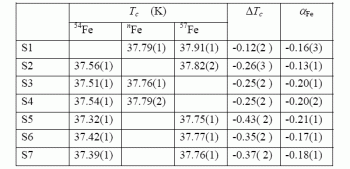
... или он так же пренебрежительно мал, как и в купратных ВТСП? Один из возможных способов решения данной проблемы связан с обнаружением (или необнаружением) изотопического эффекта по железу — веществу, объединяющие «железные» сверхпроводники в один класс. Впервые изотоп-эффект в железосодержащих ВТСП, а точнее, в поликристаллических соединениях SmFeAsO1–xFx (х = 0,15) с Tc = 40 К и Ba1–xKxFe2As2 (х ...
... Исследование процессов на границе сверхпроводника с ферромагнитным металлом привело к необычным результатам: немонотонная зависимость сверхпроводящей критической температуры многослойных структур ферромагнетик (F) - сверхпроводник (S), нетривиальное поведение магнитосопротивления SFS структур и подавление сверхпроводящих свойств в результате спин-поляризованной инжекции. В конце 1998 - начале ...
... ниобия в таблице элементов много проводников, но не сверх. А тепловые колебания их атомов практически такие же. Почему же у других металлов сверхпроводимость не обнаруживается? Тепловые колебания атомов не главный механизм сверхпроводимости! Проводимость конечно зависит от температуры. Но у меди, серебра почему-то при самых низких температурах сверхпроводимость не наблюдается, а у проводника ...
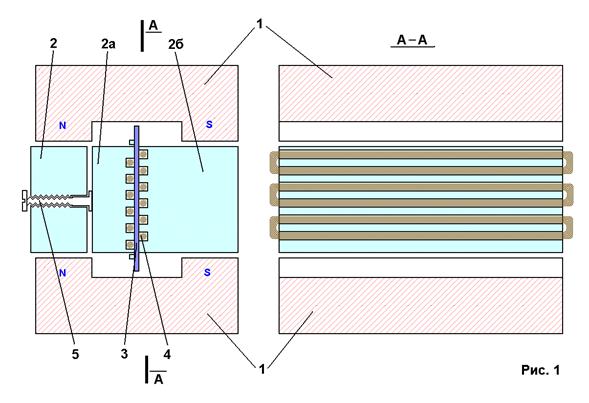
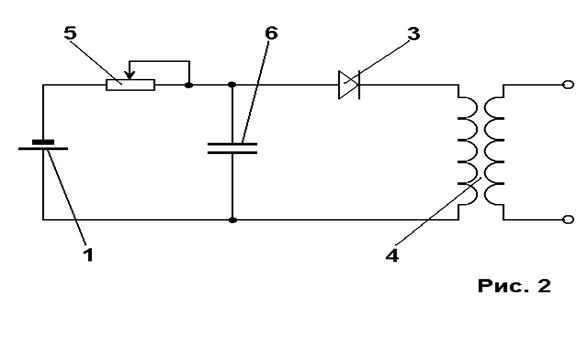
... Полное магнитное сопротивление будет определятся длиной немагнитных зазоров; Rm=L1+L2; Падение напряженности магнитного поля по участкам; Фm=H1/Rm1; H1=ФmxRm 1-первого участка, Фm=H2/Rm2; H2=ФmxRm 2-второго участка, Н1-падение напряженности магнитного поля первого участка, Н2-падение напряженности магнитного поля второго участка. Нс=Н1+Н2. Для работы устройство необходимо три ...
0 комментариев