Навигация
Туннельные эффекты
3.5 Туннельные эффекты.
Туннельный эффект известен в физики давно. Это один из основных квантово- механических эффектов и разобраться в нем можно только подходя с помощи квантового описания происходящих событий.
Представьте себе горизонтальный желоб, по которому без трения скользит массивный шарик. Что произойдет, если шарик встретит на своем пути горку – участок с наклоном? По оси абсцисс отложена координата шарика х, а по оси ординат – его потенциальная энергия.
Теряя скорость, шарик покатиться в гору. Если его начальная кинетическая энергия была больше потенциальной максимальной энергии, то она благополучно перевалит через вершину горки шарик не сможет. На склоне найдется такая «точка поворота», где вся кинетическая энергия перейдет в потенциальную, и в соответствии с законом сохранения энергии шарик остановиться, а затем покатиться обратно. Шансов проникнуть за барьер (горку) у него абсолютно никаких.
А вот квантовая частица – электрон, на пути которого возникает преграда, в аналогичной ситуации все же как-то «умудряется» просочиться через барьер.
Попытаемся внести в этот абстрактный о до некоторой степени противоречащий нашему здравому смыслу ввести хотя бы некоторый элемент наглядности. Невозможность проникновения частицы (в нашем случае шарика) в область за барьером можно уподобить известному в оптике явлению полного внутреннего отражения. Согласно геометрической оптике лучи, подающие под углом больше предельного не проникают не проникают из среда оптически более плотной, в среду, оптически менее плотную.
Однако более подробное рассмотрение этого явления, основанная на законах не геометрической, а волновой оптике, приводит к возможности проникновения света во вторую среду. При этом если оптически более плотная среда представляет собой тонкую пластину, то световая волна проходит сквозь неё, несмотря на то что угол падения больше предельного.
А теперь вспомним о двойственной природе электрона. Частица в квантовой механике – это не совсем обычный шарик, пусть даже сверхмалых размеров, она даже обладает и волновыми двойствами, а волна, как мы выяснили, все же слегка проникает в запретную область, она как бы проверяет возможность проникновения в эту среду. При этом амплитуда затухает и тем быстрее, или говорят иначе, чем выше энергетический барьер.
Выходит , что какова бы не была энергия электрона и как бы ни был высок энергетический барьер, всегда есть отличная от нуля вероятность найти электрон внутри барьера, а если барьер не очень гладок, то и за барьером, по другую сторону. Тогда на обратной стороне барьера появляется конечная амплитуда, а согласно законам квантовой механики квадрат амплитуды и определяет вероятность того, что электрон будет здесь найден, если провести соответствующие эксперименты.
При этом электроны «пробивают» только строго горизонтальные туннели, на выходе из которых полная энергия частиц точно такая же, как и на входе. Тунелирование возможно только в том случае, если уровни, на которые переходят электроны, не заняты, и то в противном случае запрет Паули.
Итак, не имея достаточной энергии, чтобы перескочить через преграду, как бы «порывает» туннель в его недрах. Вероятность такого перехода, или как говорят физики, прозрачность энергии зависит от энергии электрона и очень сильно от ширины и высоты барьера. Туннельный эффект становиться наблюдаем лишь при толщинах барьеров, меньших 100 Å, так что у применяемых электрических изоляционных покрытий громадный запас прочности в отношении туннельного тока.
3.6 Эффект Джозефсона.
Если туннельный контакт двух сверхпроводников включить во внешнюю цепь с источником тока и устанавливается такой, чтобы удовлетворить соотношению I= I0sinj, где j - разность фаз, по обе стороны заряда в некоторой его точке, а I0 - максимальный туннельный ток, пропорциональный площади туннельного перехода и прозрачность барьера. Но обратим внимание на то, что в это выражение для тока никак не входит напряжение на контакте. При нулевой разности через туннельный контакт, образованный двумя сверхпроводниками разделенных слоем диэлектрика, может проникать постоянный ток. Это явление называют стационарным явлением Джозефсона. Вольт – амперная характеристика джозефсонского туннельного контакта показана на рисунке14. Вертикальная черточка при U = 0 и есть ток, предсказываемый соотношением Джозефсона. Зависимость полного тока через переход от магнитного поля весьма своеобразна – она периодична по полю и имеет вид, изображенный на рисунке 15 .
Здесь мы сталкиваемся с явлением квантование магнитного потока в сверхпроводниках. Ток исчезает всякий раз, когда переход содержит целое число квантов магнитного потока Ф0 , и достигает максимума соответственно при половинном, полуторном и другие значения магнитного потока Ф0. С ростом числа квантов ток в максимуме становиться все меньше.
Посмотрим теперь, что произойдет, если к джозефсонскому туннельному контакту приложить постоянную разность потенциалов. Для этого случая Джозефсон предсказал ещё более удивительные эффекты, а именно при появлении постоянного напряжения I на туннельном контакте через него должен идти высокочастотный переменный ток – это явление называют стационарным явлением Джозефсона.
Частоту переменного джозефсонского тока легко подсчитать. При наличии разности потенциалов между двумя сверхпроводниками энергия двух систем куперовских пар по обе стороны от перехода отличаются на величину DЕ = 2еU (2е – заряд пары). Именно такое количество может получить пар от источника напряжения при прохождении через диэлектрический слой. При протекании сверхпроводящего тока не требуется затрат в энергии, и полученная куперовской парой пропорция 2еU излучается в виде кванта с энергией hn = 2еU. Это излучение с частотой n = 2еU\h и было зарегистрировано в экспериментальных с контактами Джозефсона. Но излучать электромагнитные волны может только переменный ток – именно такой ток и течет через джозефсонский туннельный контакт.
Отметим одно преципиальное техническое достоинство. Даже при очень малых напряжениях джозефсонский туннельный контакт вырабатывает такие частоты, которые не всегда легко получить другими известными способами.
Экспериментально обнаружить нестационарный эффект оказалось значительно труднее, чем постоянный ток Джозефсона. Чрезвычайно малой мощности и очень высокая частота излучения, генерируемого туннельным контактом, усложняли и без того не легкую экспериментальную задачу.
Похожие работы
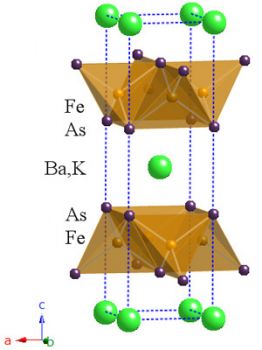
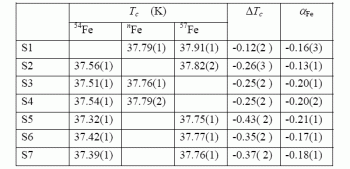
... или он так же пренебрежительно мал, как и в купратных ВТСП? Один из возможных способов решения данной проблемы связан с обнаружением (или необнаружением) изотопического эффекта по железу — веществу, объединяющие «железные» сверхпроводники в один класс. Впервые изотоп-эффект в железосодержащих ВТСП, а точнее, в поликристаллических соединениях SmFeAsO1–xFx (х = 0,15) с Tc = 40 К и Ba1–xKxFe2As2 (х ...
... Исследование процессов на границе сверхпроводника с ферромагнитным металлом привело к необычным результатам: немонотонная зависимость сверхпроводящей критической температуры многослойных структур ферромагнетик (F) - сверхпроводник (S), нетривиальное поведение магнитосопротивления SFS структур и подавление сверхпроводящих свойств в результате спин-поляризованной инжекции. В конце 1998 - начале ...
... ниобия в таблице элементов много проводников, но не сверх. А тепловые колебания их атомов практически такие же. Почему же у других металлов сверхпроводимость не обнаруживается? Тепловые колебания атомов не главный механизм сверхпроводимости! Проводимость конечно зависит от температуры. Но у меди, серебра почему-то при самых низких температурах сверхпроводимость не наблюдается, а у проводника ...
... Полное магнитное сопротивление будет определятся длиной немагнитных зазоров; Rm=L1+L2; Падение напряженности магнитного поля по участкам; Фm=H1/Rm1; H1=ФmxRm 1-первого участка, Фm=H2/Rm2; H2=ФmxRm 2-второго участка, Н1-падение напряженности магнитного поля первого участка, Н2-падение напряженности магнитного поля второго участка. Нс=Н1+Н2. Для работы устройство необходимо три ...

0 комментариев