Навигация
Метод разделения переменных или метод Фурье
1.2 Метод разделения переменных или метод Фурье
Одним из наиболее распространенных методов решения уравнений с частными производными является метод разделения переменных или метод Фурье.
Пусть требуется найти функцию ![]() , удовлетворяющую для t>0 уравнению
, удовлетворяющую для t>0 уравнению
|
в области D и дополнительным начальным и граничным условиям, где ![]() дифференциальное уравнение с частными производными второго порядка.
дифференциальное уравнение с частными производными второго порядка.
Попытаемся с помощью суперпозиции всех линейно независимых частных решений описанного типа (т. е. удовлетворяющих граничному условию) удовлетворить и начальным условиям. Для этого будем искать нетривиальные частные решения уравнения (1.2.1), удовлетворяющие граничным условиям, в классе функций вида ![]() (где
(где ![]() непрерывны в
непрерывны в ![]() ,
, ![]() непрерывны в
непрерывны в ![]() ). Подставляя функцию
). Подставляя функцию ![]() в уравнение (1.2.1) и деля обе части уравнения на
в уравнение (1.2.1) и деля обе части уравнения на ![]() , получаем
, получаем
![]() .
.
Чтобы это равенство было тождественно (т.е. чтобы функция ![]() удовлетворяла уравнению (1.2.1) при всех
удовлетворяла уравнению (1.2.1) при всех ![]() ) необходимо и достаточно, чтобы обе дроби были равны одной и той же константе
) необходимо и достаточно, чтобы обе дроби были равны одной и той же константе
![]() .
.
|
![]() ,
,
|
причем функция ![]() должна удовлетворять граничным условиям. Соответствующая краевая задача для уравнения (1.2.3) имеет нетривиальные решения не при всех значениях
должна удовлетворять граничным условиям. Соответствующая краевая задача для уравнения (1.2.3) имеет нетривиальные решения не при всех значениях![]() . Те значения
. Те значения ![]() , при которых она будет иметь нетривиальные решения, называются собственными значениями краевой задачи, а соответствующие им решения
, при которых она будет иметь нетривиальные решения, называются собственными значениями краевой задачи, а соответствующие им решения ![]() уравнения (1.2.3) – собственными функциями краевой задачи.
уравнения (1.2.3) – собственными функциями краевой задачи.
Суть метода Фурье:
1) ищем решение уравнения (1.2.1), удовлетворяющее только граничным условиям, среди функций вида ![]() . Для функции
. Для функции ![]() получаем краевую задачу;
получаем краевую задачу;
2) решаем краевую задачу для функции ![]() . Пусть
. Пусть ![]() суть собственные функции этой задачи, а
суть собственные функции этой задачи, а ![]() - отвечающие им собственные значения;
- отвечающие им собственные значения;
3) для каждого собственного значения ![]() находим решение уравнения (1.2.3);
находим решение уравнения (1.2.3);
4) таким образом, частным решением уравнения (1.2.1), удовлетворяющим только граничному условию, являются функции вида ![]() ;
;
5) возьмем сумму таких частных решений по всем собственным функциям ![]() .Данная функция будет являться общим решением рассматриваемой задачи. Причем коэффициенты выбираются таким образом, чтобы эти суммы были решениями начальной задачи [2].
.Данная функция будет являться общим решением рассматриваемой задачи. Причем коэффициенты выбираются таким образом, чтобы эти суммы были решениями начальной задачи [2].
1.3 Однородные линейные уравнения второго порядка с постоянными коэффициентами
При решении задач математической физики часто приходят к линейным дифференциальным уравнениям второго порядка. Уравнение
|
является однородным линейным уравнением второго порядка с коэффициентом при старшей производной равным единице, а ![]() . Рассмотрим решение уравнения (1.3.1), оно может быть сведено к алгебраическим операциям и получено в элементарных функциях.
. Рассмотрим решение уравнения (1.3.1), оно может быть сведено к алгебраическим операциям и получено в элементарных функциях.
В силу общих свойств линейного уравнения, нам достаточно найти два частных решения, образующих фундаментальную систему решений.
Покажем, что выражение
|
где ![]() – действительное число, будет удовлетворять нашему уравнению.
– действительное число, будет удовлетворять нашему уравнению.
Продифференцируем по x выражение (1.3.2):
![]() .
.
Подставляем полученные выражения в (1.3.1):
|
Обозначим через ![]() - это есть характеристический многочлен, соответствующий оператору L. Тогда (1.3.3) запишется в виде
- это есть характеристический многочлен, соответствующий оператору L. Тогда (1.3.3) запишется в виде ![]() .
.
Характеристический многочлен получается из оператора L[y], если производные различных порядков в этом уравнении заменить равными степенями величины ![]() :
: ![]() на
на ![]() .
.
|
![]() .
.
Уравнение (1.3.4) – есть алгебраическое уравнение с неизвестным ![]() , оно называется характеристическим уравнением. Если мы в качестве постоянной
, оно называется характеристическим уравнением. Если мы в качестве постоянной ![]() в выражение
в выражение ![]() возьмем корень
возьмем корень ![]() характеристического уравнения (1.3.4), то
характеристического уравнения (1.3.4), то ![]() , т.е.
, т.е. ![]() будет решением дифференциального уравнения (1.3.1).
будет решением дифференциального уравнения (1.3.1).
Уравнение (1.3.4) – уравнение 2-ой степени, следовательно, имеет 2 корня. Если все корни различны, то каждый из них соответствует частному решению дифференциального уравнения (1.3.1).
![]()
Следовательно, общее решение уравнения (1.3.1) будет
![]() ,
,
где ![]() - произвольные постоянные, а
- произвольные постоянные, а ![]() - решения характеристического уравнения (1.3.4) [6].
- решения характеристического уравнения (1.3.4) [6].
|
![]() .
.
Если корни характеристического уравнения чисто мнимые, т.е. ![]() . Общим решением уравнения (1.3.1) будет
. Общим решением уравнения (1.3.1) будет
|
Если предположить, что характеристическое уравнение имеет равные корни ![]() , то одно частное решение будет иметь вид
, то одно частное решение будет иметь вид
![]() .
.
Второе частное решение будет
![]() .
.
Тогда общее решение уравнения (1.3.1) можно представить в виде
|
Глава II Нахождение функции, описывающей собственные колебания мембраны
Похожие работы
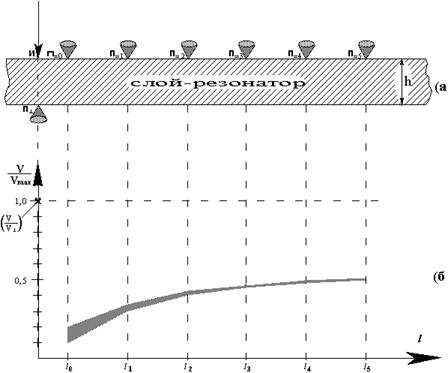
... сигнала от этого нарушения. Таким образом, выделяя участок спектра сейсмосигнала около собственной частоты этого слоя, можно выявить зону его нарушения. Описанную здесь модель распространения поля упругих колебаний при сейсморазведочных работах подтвердили, сами того не желая, ученые Института геофизики СО РАН. Их эксперимент заключается в следующем. Мощный, 100-тонный генератор гармонического ...
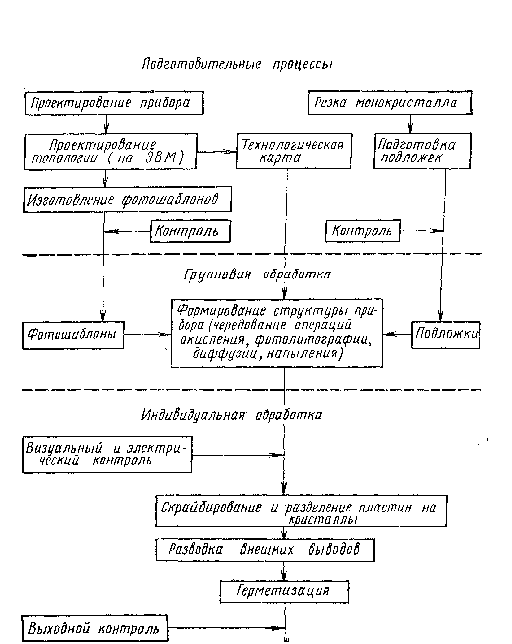
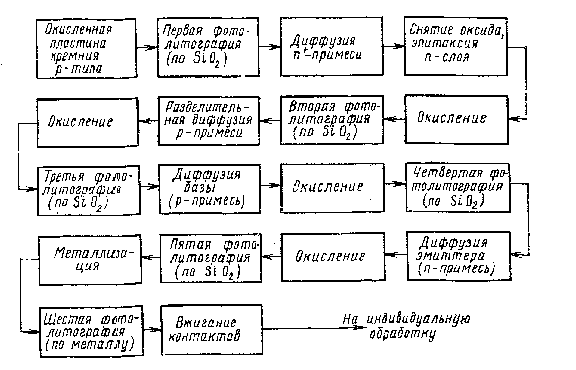
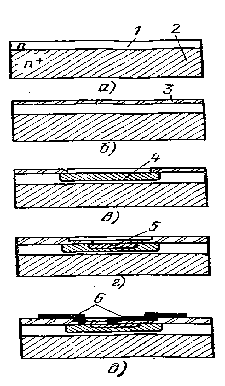
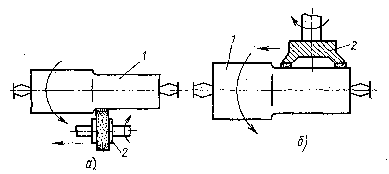
... - внутренняя и наружная шестерни, 4 - сепараторы , 5 - пластины По характеру воздействия абразива на полупроводниковые пластины различают шлифование свободным и связанным абразивом. В зависимости от зернистости используемого абразива, режимов обработки и качества полученной поверхности различают предварительное (черновое) и окончательное (чистовое) шлифование. Шлифование свободным абразивом ...
... 84,4 29 1,7 3,9 15,4 54,5 119,4 210,3 327,1 469,8 833,2 30 35,8 36 37,3 41,4 47,6 55,1 63,4 72,3 91,1 31 2,1 4,4 13,8 41,4 86,4 149,1 229,6 328,1 578,5 2. Расчет прочности печатных плат В соответствии с общей методикой прочностных расчетов для оценки прочности печатной платы необходимо в первую очередь рассчитать основную частоту собственных колебаний платы. ...
... с использованием вновь изученного материала. 1.2 Развитие познавательного интереса к физике при использовании компьютерных технологий Глава 2 Компьютерное моделирование электромагнитных колебаний 2.1 Возможности применения графических пакетов при изучении электромагнитных колебаний в курсе физики средней школы На сегодняшний день разработано множество графических пакетов и оболочек (Соrel, ...
0 комментариев