Навигация
Собственные колебания круглой мембраны
2.3 Собственные колебания круглой мембраны
Сравним теперь результаты решения двух задач о нахождении функции, характеризующей прогиб мембраны, также при заданных различных граничных условиях, одинаковых начальных условиях, но уже для круглой мембраны.
|
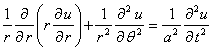 .
.
Будем искать решение этого уравнения при заданных начальных условиях
|
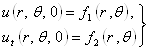
|
![]() .
.
Применим метод разделения переменных. Пусть
![]() .
.
Подставляем полученное выражение для функции ![]() в уравнение (2.3.1), получаем:
в уравнение (2.3.1), получаем:
![]() .
.
|
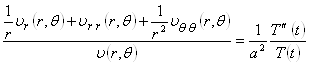 .
.
Из соотношения (2.3.4) получаем однородное дифференциальное уравнение второго порядка для функции ![]()
![]() ,
,
|
![]() ,
,
и следующую задачу на собственные значения для функции ![]() :
:
|

К задаче (2.3.6) снова применим метод Фурье для нахождения функции ![]() . Пусть
. Пусть ![]() , подставляем в уравнение для функции
, подставляем в уравнение для функции ![]() .
.
![]()
Поделим данное равенство на ![]() :
:
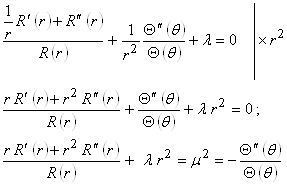
Так как левая часть соотношения (![]() ) функция только переменной r, а правая (
) функция только переменной r, а правая (![]() ) - только переменной
) - только переменной ![]() , то равенство должно сохранять постоянное значение, пусть оно равно
, то равенство должно сохранять постоянное значение, пусть оно равно ![]() . При данном предположении получаем:
. При данном предположении получаем:
1) однородное дифференциальное уравнение второго порядка для нахождения функции ![]() :
:
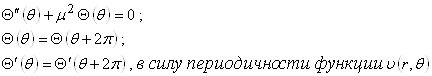
Нетривиальные периодические решения для ![]() существуют лишь при
существуют лишь при ![]() и имеют вид (см. 2.2):
и имеют вид (см. 2.2):
![]() .
.
2) уравнение для определения функции ![]()
|

|
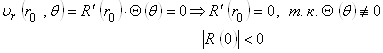
Таким образом, требуется решить задачу о собственных значениях.
Введем новую переменную
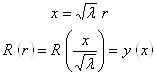
Подставляем выражение ![]() в уравнение для определения функции
в уравнение для определения функции ![]() и получаем, что данное уравнение есть уравнение цилиндрической функции n-го порядка.
и получаем, что данное уравнение есть уравнение цилиндрической функции n-го порядка.
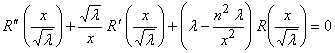
|

Решение предыдущей задачи сводится к решению цилиндрического уравнения (2.3.9) с дополнительными граничными условиями
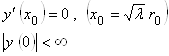 ,
,
общее решение, которого имеет вид
![]() ,
,
где ![]()
![]() - функция Бесселя первого рода,
- функция Бесселя первого рода, ![]() - функция Бесселя второго рода или функция Неймана (смотри приложение).
- функция Бесселя второго рода или функция Неймана (смотри приложение).
Из условия ![]() следует, что
следует, что ![]() , т. к. при
, т. к. при ![]() .
.
Из условия ![]() имеем
имеем
![]() , где
, где ![]() .
.
Это трансцендентное уравнение имеет бесчисленное множество вещественных корней ![]() , т.е. уравнение (2.3.7) имеет бесчисленное множество собственных значений
, т.е. уравнение (2.3.7) имеет бесчисленное множество собственных значений
 ,
,
|
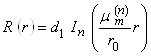
краевой задачи для нахождения функции ![]() . Всякое нетривиальное решение рассматриваемой краевой задачи дается формулой (2.3.10).
. Всякое нетривиальное решение рассматриваемой краевой задачи дается формулой (2.3.10).
Найдем норму собственных функций и получим условие ортогональности системы собственных функций 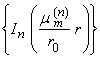 с весом r:
с весом r:
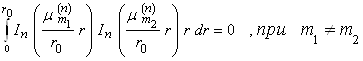
Для этого рассмотрим функции
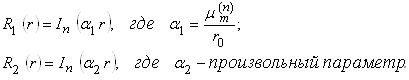
Они удовлетворяют уравнениям
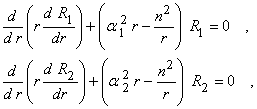
причем ![]() , а
, а ![]() не удовлетворяет этому граничному условию. Вычтем из первого уравнения второе, предварительно умножив их, соответственно, на
не удовлетворяет этому граничному условию. Вычтем из первого уравнения второе, предварительно умножив их, соответственно, на ![]() и
и ![]() .
.
|
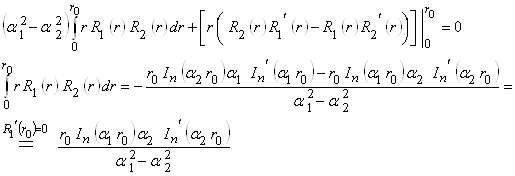
Переходя к пределу при ![]() , получаем неопределенность
, получаем неопределенность 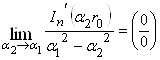 . Раскрывая неопределенность по правилу Лопиталя
. Раскрывая неопределенность по правилу Лопиталя
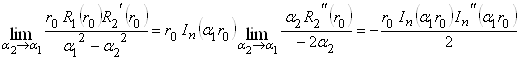 ,
,
получаем выражение для квадрата нормы:
|
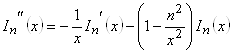 , то
, то 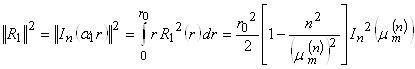 .
.
Итак, получаем:
1. Согласно (2.3.11) при ![]() , собственные функции
, собственные функции ![]() , принадлежащие различным собственным значениям
, принадлежащие различным собственным значениям ![]() , ортогональны с весом r .
, ортогональны с весом r .
Похожие работы
... сигнала от этого нарушения. Таким образом, выделяя участок спектра сейсмосигнала около собственной частоты этого слоя, можно выявить зону его нарушения. Описанную здесь модель распространения поля упругих колебаний при сейсморазведочных работах подтвердили, сами того не желая, ученые Института геофизики СО РАН. Их эксперимент заключается в следующем. Мощный, 100-тонный генератор гармонического ...
... - внутренняя и наружная шестерни, 4 - сепараторы , 5 - пластины По характеру воздействия абразива на полупроводниковые пластины различают шлифование свободным и связанным абразивом. В зависимости от зернистости используемого абразива, режимов обработки и качества полученной поверхности различают предварительное (черновое) и окончательное (чистовое) шлифование. Шлифование свободным абразивом ...
... 84,4 29 1,7 3,9 15,4 54,5 119,4 210,3 327,1 469,8 833,2 30 35,8 36 37,3 41,4 47,6 55,1 63,4 72,3 91,1 31 2,1 4,4 13,8 41,4 86,4 149,1 229,6 328,1 578,5 2. Расчет прочности печатных плат В соответствии с общей методикой прочностных расчетов для оценки прочности печатной платы необходимо в первую очередь рассчитать основную частоту собственных колебаний платы. ...
... с использованием вновь изученного материала. 1.2 Развитие познавательного интереса к физике при использовании компьютерных технологий Глава 2 Компьютерное моделирование электромагнитных колебаний 2.1 Возможности применения графических пакетов при изучении электромагнитных колебаний в курсе физики средней школы На сегодняшний день разработано множество графических пакетов и оболочек (Соrel, ...
0 комментариев