Навигация
Ионизация системы газ – частицы в модели Гибсона
3.1. Ионизация системы газ – частицы в модели Гибсона.
В состоянии термодинамического равновесия распределение потенциала ![]() и объемного заряда
и объемного заряда ![]() тесно связаны между собой и подчинены уравнению Пуассона (2.1.2). Термоионизационное равновесие системы газ – частицы будет полностью определено, если одновременно найдены оба распределения: заряда ρ и потенциала φ. Таким образом, описать ионизацию в плазме газ – частицы – значит решить уравнение Пуассона при некоторых упрощающих предположениях, используемых в модели.
тесно связаны между собой и подчинены уравнению Пуассона (2.1.2). Термоионизационное равновесие системы газ – частицы будет полностью определено, если одновременно найдены оба распределения: заряда ρ и потенциала φ. Таким образом, описать ионизацию в плазме газ – частицы – значит решить уравнение Пуассона при некоторых упрощающих предположениях, используемых в модели.
В [20] предполагается, что в плазмозоле идентичных частиц (в системе макрочастицы + излученные ими электроны + электрически и химически нейтральный буферный газ) в состоянии термодинамического равновесия наблюдается однородная ионизация дисперсных частиц (все частицы К-фазы имеют один и тот же заряд q=ze, z – зарядовое число, е – элементарный заряд). Плазма электрически нейтральна, а распределения объемного заряда электронов и потенциала в плазме связаны больцмановским коэффициентом, т.е. электроны в поле частиц распределены по Больцману:
![]() ,
(3.1.1)
,
(3.1.1)
где r – расстояние от центра макрочастицы; neb – концентрация электронов на расстоянии b от выделенной КЧ; ![]() - электростатический потенциал; k – постоянная Больцмана; T – температура; b – радиус сферически-симметричной ячейки, в которой, согласно основному допущению модели [20], частица КДФ оказывается полностью за экранированной электронным газом, т.е.
- электростатический потенциал; k – постоянная Больцмана; T – температура; b – радиус сферически-симметричной ячейки, в которой, согласно основному допущению модели [20], частица КДФ оказывается полностью за экранированной электронным газом, т.е.
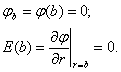 (3.1.2)
(3.1.2)
Радиус b определяется объемом, отведенным в плазмозоле на одну дисперсную частицу:
![]() . (3.1.3)
. (3.1.3)
Связь электронной плотности в ячейке с распределением электростатического потенциала ![]() задается уравнением (2.1.2), которое запишем:
задается уравнением (2.1.2), которое запишем:
![]() . (3.1.4)
. (3.1.4)
Учитывая граничные условия (3.1.2), имеем задачу Коши. Ее решение ![]() параметрически зависит от концентрации электронов на границе ячейки neb. Если при этом известна электронная концентрация на поверхности КЧ, т.е. для r=rp – радиусу частиц конденсата, приходим к замкнутой системе уравнений для определения концентрации электронов в плазме. Действительно, из уравнения Пуассона (3.1.4) находим параметрическую зависимость потенциала в ячейке от neb. Подставляя эту зависимость в распределение Больцмана (3.1.1) и учитывая, что
параметрически зависит от концентрации электронов на границе ячейки neb. Если при этом известна электронная концентрация на поверхности КЧ, т.е. для r=rp – радиусу частиц конденсата, приходим к замкнутой системе уравнений для определения концентрации электронов в плазме. Действительно, из уравнения Пуассона (3.1.4) находим параметрическую зависимость потенциала в ячейке от neb. Подставляя эту зависимость в распределение Больцмана (3.1.1) и учитывая, что ![]() , можно в символическом виде записать
, можно в символическом виде записать
![]() .
(3.1.5)
.
(3.1.5)
Таким образом, получили трансцендентное уравнение относительной переменной neb. Разрешив его относительно neb и подставив neb в уравнение, выражающее факт электронейтральности ячейки, получим значение среднего заряда КЧ в плазме:
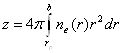 . (3.1.6)
. (3.1.6)
Окончательно средняя по объему концентрация электронов в плазмозоле:
![]() . (3.1.7)
. (3.1.7)
Изложенная последовательность шагов расчета ионизации плазмозоля дает возможность строить конкретные алгоритмы числовых расчетов, предполагающих их реализацию на ЭВМ. Расчеты, приведенные в [20] реализованы на основе подпрограмм, содержащих в своей основе три основных момента: вычисление зависимости ![]() ; определение концентрации электронов на границе ячейки решением трансцендентного уравнения относительно neb; вычисление заряда КДФ – z и средней концентрации электронов в объеме плазмозоля – ne. Концентрация электронов на внутренней границе ячейки в модели определяется законом термоэмиссии Ричардсона-Дешмана:
; определение концентрации электронов на границе ячейки решением трансцендентного уравнения относительно neb; вычисление заряда КДФ – z и средней концентрации электронов в объеме плазмозоля – ne. Концентрация электронов на внутренней границе ячейки в модели определяется законом термоэмиссии Ричардсона-Дешмана:
![]() . (3.1.8)
. (3.1.8)
Здесь К – коэффициент коррекции, учитывающий свойства поверхности КЧ (содержит коэффициент отражения электронов поверхностью дисперсных частиц); В=4,83·1021К-3/2.
Похожие работы
... (гаммексана, или линдана, ценного инсектицида), алкансульфонатов (поверхностно-активных добавок и эмульгаторов), капролактама (одного из предшественников найлона). Новые направления в фотохимии. Лазерная нанотехнология Позиционирование атомов фокусированным лазерным лучом Все компьютерные микропроцессоры изготавливаются на кремниевой подложке методом фотолитографии (см. выше, фоторезисты). ...

0 комментариев