Навигация
Электроемкость. Конденсаторы. Емкость плоского конденсатора
6. Электроемкость. Конденсаторы. Емкость плоского конденсатора
Потенциал уединенного проводника пропорционален сообщенному ему заряду, поэтому отношение заряда проводника к его потенциалу не зависит от заряда и является характеристикой данного проводника.
Электроемкостью уединенного проводника называют величину, равную отношению заряда проводника к потенциалу этого проводника.
![]()
![]()
![]() .
.
На практике применяются ![]()
Электроемкость проводника не зависит от вещества, из которого он изготовлен, а зависит от его формы, размеров и диэлектрической проницаемости среды, в которой находится этот проводник.
Используя формулу потенциала электрического поля, созданного равномерно заряженным шаром
![]() , для емкости шара получим
, для емкости шара получим 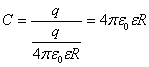 .
.
КОНДЕНСАТОРЫ
Уединенные проводники обладают малой емкостью. На практике возникает потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе значительные заряды.
Конденсатором называют систему, состоящую из двух разделенных диэлектриком проводников, на которых могут накапливаться заряды противоположных знаков.
Проводники, образующие конденсатор, называют обкладками.
Чтобы внешние тела не влияли на емкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было полностью сосредоточено внутри конденсатора. Этому условию удовлетворяют две близко расположенные пластины, два коаксиальных цилиндра и две концентрические сферы.
Емкостью конденсатора называют величину, равную отношению заряда конденсатора к разности потенциалов (напряжению) между его обкладками
![]() =
=![]() .
.
ЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
Напряженность поля между обкладками плоского конденсатора
![]() .
.
Для однородного поля справедливо соотношение
![]() .
.
Следовательно, емкость плоского конденсатора
![]()
(S – площадь обкладок, d – расстояние между обкладками).
7. Соединение конденсаторов. Энергия заряженного конденсатора
При параллельном соединении конденсаторов напряжения на каждом конденсаторе одинаковы и равны напряжению на клеммах батареи
![]() .
.
Заряд батареи
![]() .
.
Исходя из того, что ![]() , имеем
, имеем
![]() ,
,
поэтому
![]() .
.
При последовательном соединении конденсаторов
![]() ,
, ![]() .
.
Учитывая, что ![]() , имеем
, имеем
![]() ,
,
поэтому при последовательном соединении конденсаторов
![]() .
.
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
При зарядке конденсатора совершается работа по перемещению электрических зарядов против сил электрического поля. При перемещении заряда ![]() совершается работа
совершается работа ![]() . Учитывая, что
. Учитывая, что ![]() , получим
, получим ![]() . Следовательно,
. Следовательно,
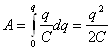 .
.
По закону сохранения энергии эта работа равна энергии заряженного конденсатора, т.е.
![]() .
.
Используя формулы ![]() и
и ![]() , получим
, получим
![]() и
и ![]() .
.
Похожие работы
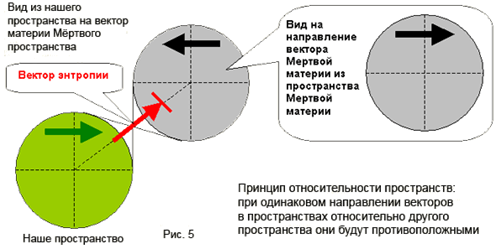
... Эйнштейн интерпретировал преобразования Лоренца кинетически, т.е. как характеризующие свойства движения в пространстве и времени, тем самым заложив основы теории относительности. Он снял проблему эфира, упразднив его, радикально изменил классические представления о пространстве и времени. Явления, описываемые теорией относительности, называются релятивистскими (от латинского - относительный) и ...
... подобием нейтрона, оставаясь гравитоном для Желтой материи, а позитрон приобретает положительный заряд и все качества, присущие протону в нашем пространстве. Это ЕДИНЫЙ ЗАКОН МАТЕРИИ ВСЕЛЕННОЙ, и он правомерен во всех ее пространствах. Протон и нейтрон образуют не некое слипшееся бесформенное образование, а активную сферу сильного (ядерного) орбитального взаимодействия частиц, именуемую ядром ...
... – положительный и отрицательный. К настоящему времени существует экспериментальное доказательство существования как вещества, так и антивещества. Предсказаны и зарегистрированы нейтрино и антинейтрино [44]. Изложенные основы теории непустого эфира, отчетливо демонстрируют этот первый шаг самоорганизации вещества. Следующие шаги ведут к образованию более сложных форм материи, вплоть до создания ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...



0 комментариев