Навигация
Линейный атомный осциллятор
38891
знак
0
таблиц
9
изображений
2.1 Линейный атомный осциллятор
Взаимодействие света со средой. Причины, по которым в линейной оптике характер явлении не зависит от интенсивности излучения, можно выявить, обратившись к ее теоретическим основам. Известно, что эффекты взаимодействия света с веществом можно трактовать как на классическом, так и на квантовом языке. Квантовый язык необходим при анализе поглощения и излучения света атомными системами. При изучении же распространения света в среде в области прозрачности, то есть вдали от полос резонансного поглощения среды, вполне удовлетворительно классическое описание, которым мы и воспользуемся ниже.
Оптические свойства среды в линейной оптике описываются такими не зависящими от интенсивности волны характеристиками, как коэффициент преломления:
(1)
(
— фазовая скорость света в среде) и коэффициент поглощения 
. По мере распространения в среде вдоль оси oz световая волна затухает по закону:
(2)
Взаимодействие света со средой состоит из последовательных элементарных взаимодействий с ее атомами или молекулами. В электрическом поле волны Е атомы или молекулы среды поляризуются: отрицательно заряженные электроны под действием поля смещаются относительно положительно заряженных ядер, появляется электрический дипольный момент, причем смещение определяется величиной и знаком напряженности поля. Знак и величина напряженности светового поля изменяются с частотой 
, в связи с этим изменяется и положение электрона. Колеблющийся же электрон сам является источником поля; он переизлучает действующее на него световое поле.
Дипольный момент, приобретённый отдельным атомом под действием световой волны:
(3)
Величина 
называется линейной атомной восприимчивостью, а дипольный момент, приобретённый 1 
среды P, называется поляризацией среды:
(4)
где N – число атомов в 1 , а 
- макроскопическая линейная восприимчивость. Диэлектрическая проницаемость среды 
и показатель преломления n в силу (3) и (4) имеют вид:
(5)
(6)
Смещение атомного электрона под действием электрического поля световой волны описывается уравнением:
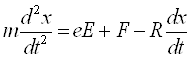(7)
Здесь m – масса электрона, e – его заряд, R – параметр, характеризующий затухание электронных колебаний, eE – сила действующая на электрон со стороны поля, F – сила, действующая на электрон со стороны атомного ядра (возвращающая сила ядра):
(8)
Уравнение гармонического осциллятора:
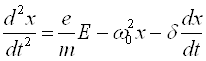(9)
где 
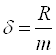, а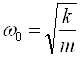 
- собственная частота атомного осциллятора.
Решение имеет вид:
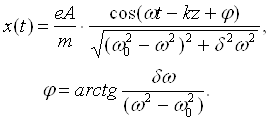(10)
Формулы (9), (10) описывают простейшие закономерности дисперсии света: показатель преломления n растёт (а фазовая скорость 
уменьшается) по мере приближения частоты световой волны 
к собственной частоте атомного осциллятора 
или, другими словами, к полосе поглощения среды.
2.2 Нелинейный атомный осциллятор. Нелинейные восприимчивости
Движение электрона в поле ядра — это движение в потенциальной яме, имеющей конечную глубину (рис. 1,а). Наглядным, хотя и грубым, аналогом движения электрона в поле ядра и соответствующей потенциальной яме может служить движение тяжелого шарика внутри сосуда, форма которого имеет форму потенциальной ямы. Если на атом воздействуют сильное световое поле 
, то форма потенциальной ямы может искажаться.
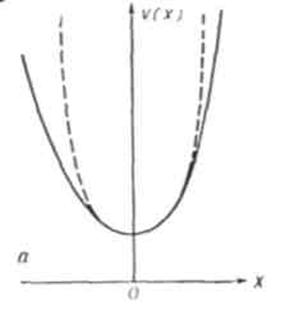
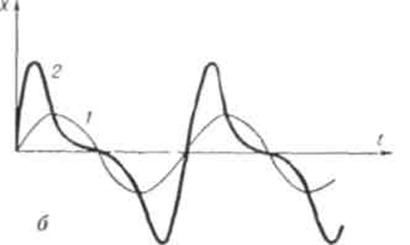
Рис. 1, а — потенциальна яма, в которой совершает колебание оптический электрон. При малых смещениях 
потенциальная яма симметрична относительно 
(пунктир), и сила, действующая на электрон со стороны ядра, пропорциональна смещению . При больших смещениях яма может оказаться несимметричной (сплошная линия), б — отклик оптического электрона, колеблющегося и потенциальной яме, на гармоническое световое поле. В слабых полях форма отклика повторяет внешнее воздействие (1), в сильных полях форма отклика искажается (2).
При этом сила F нелинейно зависит от смещения x, то есть:
(11)
В соответствии с (11) уравнение (9) становится нелинейным, а осциллятор – ангармоническим:
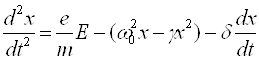(12)
Отклик такого осциллятора на гармоническом поле не повторяет форму внешнего воздействия (рис. 1, б). при ещё больших световых полях в выражении для F появляются члены 
и более высоких степеней. Происходит дальнейшее искажение отклика электрона и смещение положения равновесия.
Это приводит к нелинейной зависимости между поляризацией среды P и E. При (
)<1 P можно представить в виде разложения в ряд по параметру:
(13)
Коэффициенты 
и так далее называются нелинейными восприимчивостями (по порядку величины 
). Уравнение (13) является основой нелинейной оптики. Если на поверхность среды падает монохроматическая световая волна 
, где А – амплитуда, - частота, k – волновое число, x – координата точки вдоль направления распространения волны, t – время, то, согласно (13), поляризация среды наряду с линейным членом 
содержит ещё и нелинейный член 2-го порядка:
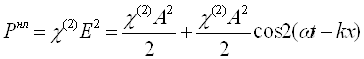. (14)
Последнее слагаемое в (14) описывает поляризацию, изменяющуюся с частотой 
, т.е. генерацию 2-й гармоники. Генерация 3-й гармоники, а также зависимость показателя преломления n от интенсивности описывается членом 
в (13) и так далее.
Похожие работы
... проблем. С помощью голографии получают пространственные изображения предметов, регистрируют (при импульсном освещении) быстропротекающие процессы, исследуют сдвиги и напряжения в телах и т.д. Оптические явления и методы, разработанные в Оптика, широко применяются для аналитических целей и контроля в самых различных областях науки и техники. Особенно большое значение имеют методы спектрального ...
... , что исследования взаимодействия лазерного излучения с веществом представляют исключительно большой научный интерес. Лазеры находят широкое применение в современных физических, химических и биологических исследованиях, имеющих фундаментальный характер. Ярким примером могут служить исследования в области нелинейной оптики. Как уже отмечалось, лазерное излучение, обладающее достаточно высокой ...
... уравнений, описывающих нелинейные многоволновые процессы в распределенных механических системах, к нормальной форме. Изучаются вопросы возникновения резонанса в нелинейных многоволновых системах. Эволюционные уравнения Распространение слабонелинейных волн в упругих средах обычно описывается квазилинейными дифференциальными уравнениями с частными производными , где и - линейные ...
... для анализа, мг 5 – 10 Напряжение сети питания, В 220 Габаритные размеры, мм 800*450*600 Вес не более, кг 45 4. Применение лазерной спектроскопии в анализе объектов окружающей среды Применение метода лазерной искровой спектроскопии в экологических исследованиях. Проблема загрязнения морей приобретает все более глобальный характер. Прогрессирующее загрязнение морской воды связано со ...
0 комментариев