Навигация
Классическое объяснение явления генерации второй гармоники
38891
знак
0
таблиц
9
изображений
4.3. Классическое объяснение явления генерации второй гармоники.
До сих пор мы рассматривали генерацию второй оптической гармоники, опираясь на фотонные представления, т. е. имея в виду трехфотонный процесс, изображенный на рисунке 4. Однако нетрудно дать этому явлению также и чисто классическое объяснение.
Пусть на квадратично-нелинейную среду падает когерентная волна накачки с частотой 
:
(4.5)
Если бы среда была линейной, то её поляризация изменялась бы во времени точно так же, как волна накачки, т. е. с частотой .
(4.6)
Но в нелинейной среде поляризация содержит, в частности, вторую гармонику - слагаемое —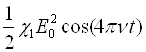 
. Изменение поляризации с частотой 
может приводить, естественно, к переизлучению света на частоте , т.е. к появлению вторичной световой волны с частотой .
Волна поляризации (в частности, вторая гармоника поляризации) распространяется в среде со скоростью волны накачки, т. е. со скоростью 
. Чтобы передача энергии от волны поляризации к переизлученной световой волне происходила эффективно, необходимо, чтобы скорости обеих волн совпадали. Так как скорость световой волны с частотой равна 
, то для переизлучения света на частоте должно выполняться условие:
(4.7)
которое, как уже известно, является условием волнового синхронизма.
Таково классическое объяснение нелинейно-оптического явления генерации второй гармоники. Заметим, что при таком объяснении роль среды как «посредника» во взаимодействии первичной и вторичной световых волн выступает весьма наглядно, так как «передача взаимодействия» идёт по «цепочке»: волна накачки — волна поляризации — вторичная световая волна.
Нетрудно представить себе процесс генерации третьей оптической гармоники. На «фотонном языке» это есть определенный четырехфотонный процесс — уничтожаются три фотона энергиями 
и рождается один фотон с энергией 
. На языке классических волновых представлений это есть результат переизлучения света, непосредственно вытекающий из факта существования третьей гармоники нелинейной поляризации среды.
Возможны также процессы генерации оптических гармоник более высоких порядков — четвертой гармоники, пятой и т. д.
Нелинейная поляризация среды позволяет осуществлять смешение частот. Пусть поляризация нелинейной среды описывается выражением:
(4.8)
Предположим, что на среду падают две когерентные световые волны с разными частотами: 
. Если сумму этих волн
(4.9)
подставить в (4.8), то в выражении, которое получится для поляризации среды, будет присутствовать, в частности, слагаемое
(4.10)
Воспользовавшись соотношением:
,
преобразуем (4.8) к следующему виду:
(4.11)
Таким образом мы видим возможность переизлучения света на частотах 
и 
. Таким образом, нелинейная поляризация среды позволяет осуществлять сложение и вычитание частот световых волн. В рассматриваемом здесь случае взаимодействие волн с частотами 
и 
может приводить, как мы видим, к появлению вторичных световых волн на частотах и .
Выражение (4.8) является наиболее простым выражением для поляризации нелинейной среды — нелинейная поляризация описывается членом, квадратичным по напряженности. В более общем случае в выражении для поляризации могут присутствовать также и члены с 
и т. д. Учет таких членов приводит к тому, что при подстановке (4.9) в выражение для поляризации появляются слагаемые с частотами: 
где n и m — целые числа. Это означает, что, кроме сложения и вычитания, возможны и другие варианты смешения частот.
Заключение
Итак, причиной любого нелинейно-оптического явления служит, в конечном счете, какое-то изменение среды, наблюдаемое при прохождении через среду достаточно мощного оптического излучения. Это изменение свойств среды следует рассматривать как определенный отклик среды на световую волну.
Природа «отклика» может быть разной. Обычно различают два типа «откликов»: поляризационный «отклик» и «отклик заселенности уровней».
Поляризационный «отклик» связан с появлением нелинейной поляризации среды под воздействием исходной световой волны. При этом внутри среды происходят процессы переориентации электрических дипольных моментов, возникают также наведенные дипольные моменты. «Инерциальнность» поляризационного отклика характеризуется малым промежутком времени – до 10-13с.
«Отклик заселенности уровней» имеет совсем иную природу. Он связан с изменением заселенностей энергетических уровней частиц среды, происходящим под воздействием световой волны, распространяющейся в среде. «Инерционность» отклика характеризуется временем, превышающим 10-8с.
Каждый из двух типов «окликов» обуславливает свою группу нелинейно-оптических явлений. Изучение природы этих двух типов «откликов» и было задачей этой курсовой работы.
Литература
1. Тарасов Л. В. Оптика, рожденная лазером. М.: ”Просвещение”, 1977
2. Лансберг Г. С. Оптика. М.: ”Просвещение”, 1977
3. Беспалов В. И., Пасманик Г. А. Нелинейная оптика. М.: “Наука”, 1980
4. Фриш С. Э. Современная оптика. М.:”Знание”, 1968
5. Вавилов С. И. Микроструктура света. М.: “Наука”,1950
6. Квантовая электроника. М.: “Советская энциклопедия”, 1969
7. Физический энциклопедический словарь Том 1. М.: “Советская энциклопедия”,1990
Похожие работы
... проблем. С помощью голографии получают пространственные изображения предметов, регистрируют (при импульсном освещении) быстропротекающие процессы, исследуют сдвиги и напряжения в телах и т.д. Оптические явления и методы, разработанные в Оптика, широко применяются для аналитических целей и контроля в самых различных областях науки и техники. Особенно большое значение имеют методы спектрального ...
... , что исследования взаимодействия лазерного излучения с веществом представляют исключительно большой научный интерес. Лазеры находят широкое применение в современных физических, химических и биологических исследованиях, имеющих фундаментальный характер. Ярким примером могут служить исследования в области нелинейной оптики. Как уже отмечалось, лазерное излучение, обладающее достаточно высокой ...
... уравнений, описывающих нелинейные многоволновые процессы в распределенных механических системах, к нормальной форме. Изучаются вопросы возникновения резонанса в нелинейных многоволновых системах. Эволюционные уравнения Распространение слабонелинейных волн в упругих средах обычно описывается квазилинейными дифференциальными уравнениями с частными производными , где и - линейные ...
... для анализа, мг 5 – 10 Напряжение сети питания, В 220 Габаритные размеры, мм 800*450*600 Вес не более, кг 45 4. Применение лазерной спектроскопии в анализе объектов окружающей среды Применение метода лазерной искровой спектроскопии в экологических исследованиях. Проблема загрязнения морей приобретает все более глобальный характер. Прогрессирующее загрязнение морской воды связано со ...
0 комментариев